Уравнение прямой на плоскости

Любую прямую на плоскости можно задать уравнением прямой первой степени вида

A x+ B y + C = 0

где A и B не могут быть одновременно равны нулю.

Уравнение прямой с угловым коэффициентом

Общее уравнение прямой при B≠0 можно привести к виду

y = k x + b

где k - угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ

Уравнение прямой в отрезках на осях

Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0, b), то она может быть найдена используя формулу уравнения прямой в отрезках

x	+	y	= 1
a	b

Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки A(x₁, y₁) и B(x₂, y₂), такие что x₁ ≠ x₂ и y₁ ≠ y₂ тоуравнение прямой можно найти, используя следующую формулу

x- x1	=	y- y1
x2 - x1	y2 - y1

Параметрическое уравнение прямой на плоскости

Параметрические уравнения прямой могут быть записаны следующим образом

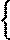	x=l t+x0
y= m t+ y0

где (x₀, y₀) - координаты точки лежащей на прямой, {l, m}- координаты направляющего вектора прямой.

Каноническое уравнение прямой на плоскости

Если известны координаты точки A(x₀, y₀) лежащей на прямой и направляющего вектора n = {l; m}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу

x - x0	=	y - y0
l	m

Гусев Серега

6) КОЛЛИНЕАРНЫЕ ВЕКТОРЫ - векторы, лежащие на одной прямой или на параллельных прямых.

Векторы называются компланарными, если имеются равные им вектора, параллельные одной плоскости.

Любые два вектора компланарны. Любые три вектора, среди которых есть два коллинеарных, компланарны.

25) Расстояние между двумя скрещивающимися прямыми в координатах

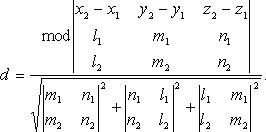
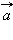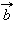44) Скалярное произведение; Скалярным произведением векторов и называется произведение их длин на косинус угла между ними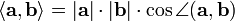

Свойства:

§ теорема косинусов легко выводится с использованием скалярного произведения:

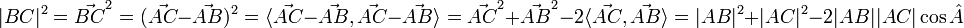
§ Угол между векторами:

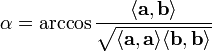
§ Оценка угла между векторами:

в формуле 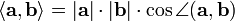знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.

§ Проекция вектора 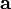на направление, определяемое единичным вектором :

,

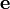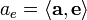§ условие ортогональности^[2] (перпендикулярности) векторов 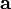и :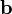

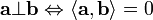
§ Площадь параллелограмма, натянутого на два вектора 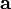и 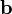, равна

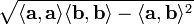
Антонов Илья

№2

Вывести формулу для вычисления расстояния между двумя скрещивающимися прямыми.

№21

Записать формулу для вычисления координат точки, делящей отрезок в данном отношении.

в трехмерном пространстве точка С, делящая отрезок АВ в заданном отношении 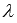, имеет координаты .

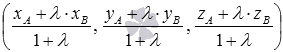№40

Сформулировать необходимое и достаточное условия компланарности трёх векторов.

Необходимым и достаточным условием компланарности трех векторов
является равенство нулю их смешанного произведения.

Зайцева Саша

9. Определение линейной комбинации системы векторов:

Линейной комбинацией векторов 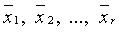называют вектор

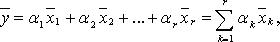
где 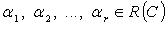- коэффициенты линейной комбинации. Если 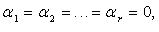комбинация называется тривиальной, если 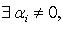- нетривиальной.

29. Формула для вычисления угла между векторами:

Cos α = (a*b ∕|a||b|)

47 . Теорема о необходимом и достаточном условии компланарности трёх векторов:

Для компланарности трех векторов 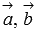и 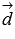трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

Основные виды уравнений плоскости в пространстве:

1. Общее уравнение плоскости

2. Уравнение плоскости в отрезках

3. Уравнение плоскости, проходящей через точку М перпендикулярно вектору нормали N

4. Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой

5. Нормальное (нормированное) уравнение плоскости.

Геометрическое значение коэффициентов A, B и C в общем уравнении плоскости Ax + By + Cz + D = 0 состоит в том, что они являются проекциями на координатные оси Ox, Oy, Oz вектора, перпендикулярного этой плоскости. А, В, С являются координатами вектора-нормали и определяют направление плоскости.