Координаты на прямой, на плоскости и в пространстве
Учреждение образования «Белорусская государственная
Сельскохозяйственная академия»
Кафедра высшей математики
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Конспект лекции для студентов бухгалтерского факультета
заочной формы получения образования (НИСПО)
Горки, 2013
Элементы векторной алгебры
Координаты на прямой, на плоскости и в пространстве
Возьмём произвольную прямую Х и выберем на ней положительное направление слева направо. На прямой возьмём произвольную точку О и назовём её началом, относительно которого будем определять положение всех точек на этой прямой. Затем выберем единицу масштаба для измерения длин. Таким образом, мы построили декартову систему координат на прямой, которую называют числовой осью или числовой прямой.
| • |
| • |
| • |
| • |
| 0 M1 M2 M x |
Пусть на числовой прямой отрезок задан точками и и указано, что точка называется началом, а точка 
концом отрезка. Такой отрезок называется направленным и обозначается . Величиной направленного отрезка называется его длина, взятая со знаком «+», если направление отрезка совпадает с направлением оси, и со знаком « » , если эти направления противоположны.
Возьмём на координатной оси точку М. Отрезок является направленным. Координатой точки М называется величина ОМ направленного отрезка . Обозначим координату точки М через х, т.е. х=ОМ. Тогда запись М(х) означает, что точка М имеет координату х.
Пусть на координатной оси даны точки и . В этом случае величина направленного отрезка . Расстояние d между точками определяется по формуле
.
Пример 1. Даны точки и . Величина направленного отрезка равна , а расстояние между точками и равно .
Положение точки на прямой определяется одним числом – её координатой, а положение точки на плоскости не может быть определено одним числом.
Возьмём на плоскости две взаимно перпендикулярные оси, пересекающиеся в точке О, зададим направление и масштаб для измерения длины. Точка О называется началом координат. Таким образом, построена декартова прямоугольная система координат на плоскости. Одна ось называется осью Ох, а другая – Оу. Называются эти оси координатными.
| • |
| • |
| x |
| Mx |
| M |
| My • |
| y |
Возьмём в прямоугольной системе координат произвольную точку М. Пусть – проекция точки М на ось Ох, проекция точки М на ось Оу. Тогда называются прямоугольными координатами точки на плоскости. Запись М(х,у) означает, что точка М имеет координаты х и у.
Пусть на плоскости в прямоугольной системе координат даны точки и . Тогда расстояние между этими точками определяется по формуле
.
Пример 2. Даны точки и . Найти расстояние между ними и расстояние от точки до начала координат.
Решение. По условию примера , , . Тогда . Расстояние от точки до начала координат равно .
Пример 3. Даны точки А(1,1), В(-3,4), С(3,12). Вычислить периметр треугольника АВС.
Решение. Периметр р треугольника АВС равен сумме длин всех его сторон. Найдём длины сторон треугольника:
,
,
.
Тогда .
Возьмём в пространстве три взаимно перпендикулярные оси, пересекающиеся в одной точке О, которая называется началом координат, и зададим единицу измерения длины (масштаб). Одна ось называется Ох (ось абсцисс), вторая – Оу (ось ординат) и третья – Oz (ось аппликат). Координатные оси, взятые попарно, определяют три взаимно перпендикулярные плоскости xOy, yOz, xOz, называемые координатными плоскостями.
| B |
| z |
| x |
| y |
| A |
| Mx |
| My |
| Mz |
| • |
| • |
| • |
| • |
| • |
| • |
| M |
Пусть М – произвольная точка пространства. Спроектируем точку М на координатные плоскости xOy и xOz (точки А и В). Проекцией точки А на ось Ох является точка , а на ось Оу – точка . Проекцией точки В на ось Oz является точка . Таким образом, точки являются проекциями точки М на координатные оси. Величины называются координатами точки М. Первая координата называется абсциссой, вторая ординатой и третья аппликатой. Запись M(x,y,z) означает, что точка М имеет координаты x, y, z.
Если в пространстве известны координаты точек и , то расстояние между ними определяется по формуле
.
Векторы. Основные понятия
Величина, которая характеризуется только своим численным значением, называется скалярной. Примерами скалярных величин являются вес, температура, площадь, длина. Величина, которая характеризуется не только своим численным значением, но и направлением, называется векторной. Примерами векторных величин являются скорость, ускорение, сила.
Вектором называется направленный отрезок, который имеет начало и конец. Если начало вектора в точке А, а конец вектора в точке В, то вектор обозначается или просто . Длина вектора равна длине отрезка, соединяющего точки А и В. Если точки А и В совпадают, то длина вектора равна нулю и вектор называется нулевым. Вектор, длина которого равна единице, называется единичным.
Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Два вектора называются равными, если они коллинеарны, имеют одинаковые длины и одинаково направлены. Из определения равенства векторов следует, что при параллельном переносе вектора получается вектор, равный исходному. Следовательно, если некоторую точку в пространстве взять за общее начало, то к этой точке можно привести все рассматриваемые векторы. Таким образом, все векторы можно рассматривать как свободные.
Если два вектора имеют одинаковые длины, коллинеарны и противоположно направлены, то они называются противоположными. Если дан вектор , то ему противоположный обозначается - .
Векторы, которые лежат в одной плоскости или в параллельных плоскостях, называются компланарными. Если компланарные векторы привести к одному началу, то они будут лежать в одной плоскости.
Пусть дана ось l и вектор . Пусть начало А вектора проектируется в точку на оси l, а конец В вектора – в точку .
 |
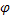| l |
| A1 |
| B1 |
| B |
| A |
Рассмотрим вектор . Проекцией вектора на ось l называется число , если направление вектора совпадает с направлением оси l, и число , если вектор и ось l имеют противоположные направления. Проекция вектора на ось l обозначается . Обозначим угол между вектором и осью l. Тогда .
В качестве оси l может быть любой вектор. Тогда можно говорить о проекции одного вектора на другой. Например, проекция вектора на вектор равна , где угол между векторами и . Иногда вместо выражения «проекция вектора на вектор » используют выражение «проекция вектора на направление вектора ».
Рассмотрим вектор в прямоугольной системе координат. Координатами вектора называются его проекции на координатные оси. Запись означает, что вектор в пространстве имеет координаты 
.
Два вектора и будут равны тогда и только тогда, когда равны их одноименные координаты, т.е.
Пусть начало вектора задано точкой , а конец вектора – точкой . Тогда для определения координат вектора от координат конца вектора вычитаются координаты его начала, т.е. .
В прямоугольной системе координат в пространстве единичные векторы осей Ox, Oy и Oz обозначим через . Эти единичные векторы называются ортами. Любой вектор в прямоугольной системе координат в пространстве может быть разложен по векторам , т.е. справедливо равенство .
Пример 4. Даны точки и . Найти координаты вектора и записать разложение этого вектора по ортам.
Решение. Если заданы координаты начала и конца вектора, то для определения координат вектора из координат его конца вычитаются координаты начала: .
Разложение вектора по ортам имеет вид: .