Законы арифметических действий над действительными числами

Тема № 1.

Действительные числа.Числовые выражения. Преобразование числовых выражений

I. Теоретический материал

Основные понятия

· Натуральные числа

· Десятичная запись числа

· Противоположные числа

· Целые числа

· Обыкновенная дробь

· Рациональные числа

· Бесконечная десятичная дробь

· Период числа, периодическая дробь

· Иррациональные числа

· Действительные числа

· Арифметические действия

· Числовое выражение

· Значение выражения

· Обращение десятичной дроби в обыкновенную

· Обращение обыкновенной дроби в десятичную

· Обращение периодической дроби в обыкновенную

· Законы арифметических действий

· Признаки делимости

Числа, употребляемые при счете предметов или для указания порядкового номера того или иного предмета среди однородных предметов, называются натуральными. Любое натуральное число можно записать с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.Такую запись чисел называют десятичной.

Например: 24; 3711; 40125.

Множество натуральных чисел принято обозначать N.

Два числа, отличающиеся друг от друга только знаком, называются противоположными числами.

Например, числа 7 и – 7.

Числа натуральные, им противоположные, а также число нуль составляют множество целыхчисел. Его принято обозначать Z.

Например: – 37; 0; 2541.

Число вида 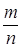, где m – целое число, n – натуральное число, называется обыкновенной дробью. Заметим, что любое натуральное число можно представить в виде дроби со знаменателем 1.

Например: , .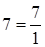

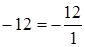Объединение множеств целых и дробных чисел (положительных и отрицательных) составляет множество рациональных чисел. Его принято обозначать Q.

Например: 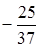; – 17,55; .

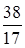Пусть дана десятичная дробь. Ее значение не изменится, если справа приписать любое число нулей.

Например: 3,47 = 3,470 = 3,4700 = 3,47000… .

Такая десятичная дробь называется бесконечной десятичной дробью.

Любую обыкновенную дробь можно представить в виде бесконечной десятичной дроби.

Последовательно повторяющаяся группа цифр после запятой в записи числа называется периодом, а бесконечная десятичная дробь, имеющая такой период в своей записи, называется периодической. Для краткости принято период записывать один раз, заключая его в круглые скобки.

Например: 0,2142857142857142857… = 0,2(142857).

2,73000… = 2,73(0).

Бесконечные десятичные непериодические дроби называются иррациональными числами.

Объединение множеств рациональных и иррациональных чисел составляет множество действительных чисел. Его принято обозначать R.

Например: 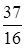; 0,(23); 41,3574…

Число 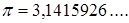является иррациональным.

Для всех чисел определены действия трёх ступеней:

· действия I ступени: сложение и вычитание;

· действия II ступени: умножение и деление;

· действия III ступени: возведение в степень и извлечение корня.

Выражение, составленное из чисел, знаков арифметических действий и скобок, называется числовым.

Например: ; .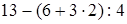

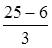Число, полученное в результате выполнения действий, называется значением выражения.

Числовое выражение не имеет смысла, если содержит деление на нуль.

При нахождении значения выражения выполняются последовательно действия III ступени, II ступени и в конце действия I ступени. При этом необходимо учитывать размещение в числовом выражении скобок.

Преобразование числового выражения заключается в последовательном выполнении арифметических действий над входящими в него числами с использованием соответствующих правил (правило сложения обыкновенных дробей с разными знаменателями, умножения десятичных дробей и др.). Задания на преобразование числовых выражений в учебных пособиях встречаются в следующих формулировках: «Найдите значение числового выражения», «Упростите числовое выражение», «Вычислите» и др.

При нахождении значений некоторых числовых выражений приходится выполнять действия с дробями разного вида: обыкновенными, десятичными, периодическими. В этом случае бывает необходимо обратить обыкновенную дробь в десятичную или выполнить обратное действие – заменить периодическую дробь обыкновенной.

Чтобы обратить десятичную дробь в обыкновенную, достаточно в числителе дроби записать число, стоящее после запятой, а в знаменателе – единицу с нулями, причем нулей должно быть столько, сколько цифр находится справа от запятой.

Например: ; .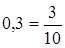

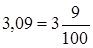Чтобы обратить обыкновенную дробь в десятичную, надо разделить ее числитель на знаменатель по правилу деления десятичной дроби на целое число.

Например: ;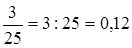

;

.

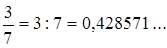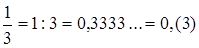Чтобы обратить периодическую дробь в обыкновенную, надо:

1) из числа, стоящего до второго периода, вычесть число, стоящее до первого периода;

2) записать эту разность числителем;

3) в знаменателе написать цифру 9 столько раз, сколько цифр в периоде;

4) дописать в знаменателе столько нулей, сколько цифр между запятой и первым периодом.

Например: ; .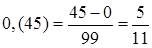

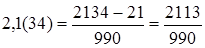Законы арифметических действий над действительными числами

1. Переместительный (коммутативный) закон сложения: от перестановки слагаемых значение суммы не меняется:

.

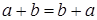2. Переместительный (коммутативный) закон умножения: от перестановки множителей значение произведения не меняется:

.

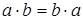3. Сочетательный (ассоциативный) закон сложения: значение суммы не изменится, если какую-либо группу слагаемых заменить их суммой:

.

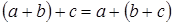4. Сочетательный (ассоциативный) закон умножения: значение произведения не изменится, если какую-либо группу множителей заменить их произведением:

.

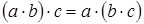5. Распределительный (дистрибутивный) закон умножения относительно сложения: чтобы умножить сумму на число, достаточно умножить каждое слагаемое на это число и сложить полученные произведения:

.

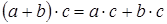6. .

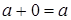7. .

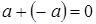8. .

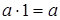9. , .

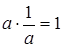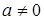10. .

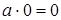Свойства 6 – 10 называют законами поглощения 0 и 1.

Признаки делимости

Свойства, позволяющие в некоторых случаях, не производя деление, определить, делится ли одно число на другое, называются признаками делимости.

Признак делимости на 2. Число делится на 2 тогда и только тогда, когда запись числа оканчивается на четную цифру. То есть на 0, 2, 4, 6, 8.

Например: 12834; –2538; 39,42.

Признак делимости на 3. Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.

Например: 2742; –17940.

Признак делимости на 4. Число, содержащее не менее трех цифр, делится на 4 тогда и только тогда, когда делится на 4 двузначное число, образованное последними двумя цифрами заданного числа.

Например: 15436; –372516.

Признак делимости на 5. Число делится на 5 тогда и только тогда, когда его последняя цифра либо 0, либо 5.

Например: 754570; –4125.

Признак делимости на 9. Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.

Например: 846; –76455.