Принципы симметрии и асимметрии

Принципы симметрии и асимметрии

НОУ ВПО Дальневосточный институт международного бизнеса

Факультет «Экономика и международный бизнес»

КОНТРОЛЬНАЯ РАБОТА

По «Концепциям современного естествознания»

ТЕМА: «Принципы симметрии и асимметрии»

Выполнила: студентка гр. 319 - БУ

Костина Е. А.

Шифр 09-БУ-08

Проверил (а): к. с. н., доцент

Зяблова Е. Ю.

Хабаровск 2009

ПЛАН РАБОТЫ

Введение 3

1. Симметрия как эстетический критерий. Операции и виды симметрии. Принципы симметрии. 5

2. Разновидность симметрии и асимметрии в природе - свойства материального мира. Понятие симметрии и асимметрии в биологии. 13

3. Золотое сечение – закон проявления гармонии природы. 26

Заключение 31

Список литературы

Введение

Первоначальный смысл симметрии – это соразмерность, сходство, подобие, порядок, ритм, согласование частей в целостной структуре. Симметрия и структура неразрывно связаны. Если некоторая система имеет структуру, то она обязательно имеет и некоторую симметрию. Идея симметрии имеет исключительное значение и как ведущее начало в осмыслении структуры естественнонаучного знания. Едва ли можно оспаривать эвристическую ценность и методологическое значение принципа симметрии. Известно, что при решении конкретных научных проблем этот принцип играет роль критерия истинности.

Симметрия является одной из наиболее фундаментальных и одной из наиболее общих закономерностей мироздания: неживой, живой природы и общества. С симметрией мы встречаемся всюду. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого знания; его широко используют все без исключения направления современной науки.

Что же такое симметрия? Почему симметрия буквально пронизывает весь окружающий нас мир? Существуют, в принципе, две группы симметрий.

К первой группе относится симметрия положений, форм, структур. Это та симметрия, которую можно непосредственно видеть. Она может быть названа геометрической симметрией.

Вторая группа характеризует симметрию физических явлений и законов природы. Эта симметрия лежит в самой основе естественнонаучной картины мира: ее можно назвать физической симметрией.

На протяжении тысячелетий в ходе общественной практики и познания законов объективной действительности человечество накопило многочисленные данные, свидетельствующие о наличии в окружающем мире двух тенденций: с одной стороны, к строгой упорядоченности, гармонии, а с другой - к их нарушению. Люди давно обратили внимание на правильность формы кристаллов, цветов, пчелиных сот и других естественных объектов и воспроизводили эту пропорциональность в произведениях искусства, в создаваемых ими предметах, через понятие симметрии.

«Симметрия, - пишет известный ученый Дж. Ньюмен, - устанавливает забавное и удивительное родство между предметами, явлениями и теориями, внешне, казалось бы, ничем не связанными: земным магнетизмом, женской вуалью, поляризованным светом, естественным отбором, теорией групп, инвариантами и преобразованиями, рабочими привычками пчел в улье, строением пространства, рисунками ваз, квантовой физикой, лепестками цветов, интерференционной картиной рентгеновских лучей, делением клеток морских ежей, равновесными конфигурациями кристаллов, романскими соборами, снежинками, музыкой, теорией относительности...".

1. Симметрия как эстетический критерий. Операции и виды симметрии. Принципы симметрии.

Одним из косвенных результатов СТО Эйнштейна явилась доказанная ею необходимость анализа, казалось бы, хорошо известных понятий, которые многие поко­ления воспринимали как нечто привычное, не требую­щее разъяснения.

В этом плане историю науки можно представить как историю попыток уточнения содержания и области при­менения научных понятий. И здесь успех всегда сопут­ствовал понятиям, которые выделялись своей эстетиче­ской привлекательностью. К таким понятиям может быть отнесена симметрия, которая с древнейших времен фигу­рировала в качестве скорее эстетического критерия, чем строго научного понятия.

Симметрия (от греч. symmetria - соразмерность) ­однородность, пропорциональность, гармония, инвари­антность структуры материального объекта относитель­но его преобразований. Это признак полноты и совер­шенства. Лишившись элементов симметрии, предмет ут­рачивает свое совершенство и красоту, т. е. эстетическое понятие.

Эстетическая окрашенность симметрии в наиболее общем понимании - это согласованность или уравнове­шенность отдельных частей объекта, объединенных в еди­ное целое, гармония пропорций. Многие народы с древ­нейших времен владели представлениями о симметрии в широком смысле как эквивалентности уравновешеннос­ти и гармонии. В геометрических орнаментах всех веков запечатлены неиссякаемая фантазия и изобретательность художников и мастеров. Их творчество было ограничено жесткими рамками, требованиями неукоснительно сле­довать принципам симметрии. Трактуемые несравненно шире, идеи симметрии нередко можно обнаружить в живописи, скульптуре, музыке, поэзии. Операции сим­метрии часто служат канонами, которым подчиняются балетные па: именно симметричные движения составля­ют основу танца. Во многих случаях именно язык сим­метрии оказывается наиболее пригодным для обсужде­ния произведений изобразительного искусства, даже если они отличаются отклонениями от симметрии или их со­здатели стремятся умышленно ее избежать.

Можно выде­лить следующие операции симметрии:

■ отражение в плоскости симметрии (отражение в зер­кале);

■ поворот вокруг оси симметрии (поворотная симметрия);

■ отражение в центре симметрии (инверсия);

■ перенос (трансляция) фигуры на расстояние;

■ винтовые повороты.

Отражение в плоскости симметрии

Отражение — это наиболее известная и чаще других встречающаяся в природе разновидность симметрии. Зеркало в точности воспроизводит то, что оно «видит», но рассмотренный порядок является обращенным: правая рука у вашего двойника в действительности окажется ле­вой, так как пальцы расположены на ней в обратном порядке. Всем, наверное, с детства знаком фильм «Ко­ролевство кривых зеркал», где имена всех героев чита­лись в обратном порядке.

Зеркальную симметрию можно обнаружить повсюду: в листьях и цветах растений, архитектуре, орнаментах. Че­ловеческое тело, если говорить лишь о наружном виде, обладает зеркальной симметрией, хотя и не вполне стро­гой. Более того, зеркальная симметрия свойственна телам почти всех живых существ, и такое совпадение отнюдь не случайно. Важность понятия зеркальной симметрии вряд ли можно переоценить.

Зеркальной симметрией обладает все, допускающее разбиение на две зеркально равные половинки. Каждая из половинок служит зеркальным отражением другой, а разделяющая их плоскость называется плоскостью зер­кального отражения, или просто зеркальной плоскостью. Эту плоскость можно назвать элементом симметрии, а со­ответствующую операцию — операцией симметрии.

Отражение в зеркале — это один из способов повто­рения фигуры, приводящий к возникновению симмет­ричного узора. Если использовать не одно, а два зеркала, то можно получить устройство, названное калейдоско­пом, открытое в 1819 г. Д. Брюстером. В калейдоскопе совмещаются два вида симметрии: зеркальная и пово­ротная. Расположив зеркала под определенным углом, можно увидеть отражение, отражение отражения и т. д. Вечно изменяющаяся череда узоров завораживает взор каждого.

Если два зеркала не пересекаются, а установлены па­раллельно друг другу, то вместо орнамента с элемента­ми, расположенными по кругу, получается бесконечный узор, который повторяется и напоминает бордюр или ленту из ткани.

С трехмерными симметричными узорами мы сталки­ваемся ежедневно: это многие современные жилые зда­ния, а иногда и целые кварталы, ящики и коробки, гро­моздящиеся на складах, атомы вещества в кристалличес­ком состоянии образуют кристаллическую решетку — элемент трехмерной симметрии. Во всех этих случаях правильное расположение позволяет экономно исполь­зовать пространство и обеспечивать устойчивость.

Поворотная симметрия

Внешний вид узора не изменится, если его повернуть на некоторый угол вокруг оси. Симметрия, возникающая при этом, называется поворотной симметрией. Примером может служить детская игра «вертушка» с поворотной сим­метрией. Во многих танцах фигуры основаны на враща­тельных движениях, нередко совершаемых только в одну сторону (т. е. без отражения), например, хороводы.

Листья и цветы многих растений обнаруживают ра­диальную симметрию. Это такая симметрия, при которой лист или цветок, поворачиваясь вокруг оси симметрии, переходит в себя. На поперечных сечениях тканей, обра­зующих корень или стебель растения, отчетливо бывает видна радиальная симметрия. Соцветия многих цветков также обладают радиальной симметрией.

Отражение в центре симметрии

Примером объекта наивысшей симметрии, характе­ризующим эту операцию симметрии, является шар. Ша­ровые формы распространены в природе достаточно ши­роко. Они обычны в атмосфере (капли тумана, облака), гидросфере (различные микроорганизмы), литосфере и космосе. Шаровую форму имеют споры и пыльца расте­ний, капли воды, выпущенной в состоянии невесомости на космическом корабле. На метагалактическом уровне наиболее крупными шаровыми структурами являются галактики шаровой формы. Чем плотнее скопление га­лактик, тем ближе оно к шаровой форме. Звездные скоп­ления — тоже шаровые формы.

Трансляция, или перенос фигуры на расстояние

Трансляция, или параллельный перенос фигуры на рас­стояние — это любой неограниченно повторяющийся узор. Она может быть одномерной, двумерной, трехмерной. Трансляция в одном и том же или противоположных на­правлениях образует одномерный узор. Трансляция по двум непараллельным направлениям образует двумерный узор. Паркетные полы, узоры на обоях, кружевные ленты, дорожки, вымощенные кирпичом или плитками, кристаллические фигуры образуют узоры, которые не имеют естественных границ.

При изучении орнаментов, используемых в книгопечатании, были обнаружены те элементы симметрии, что и в рисунке выложенных кафельными плитами полов. Орнаментальные бордюры связаны с музыкой. В музыке элементы симметричной конструкции включают в себя операции повторения (трансляции) и обращения (отра­жения). Именно эти элементы симметрии обнаружива­ются и в бордюрах.

Хотя в большинстве случаев музыка не отличается строгой симметрией, в основе многих музыкальных про­изведений лежат операции симметрии. Особенно замет­ны они в детских песенках, которые, видимо, поэтому так легко и запоминаются. Операции симметрии обна­руживаются в музыке средневековья и Возрождения, в музыке эпохи барокко (нередко в весьма изощренной форме). Во времена И. С. Баха, когда симметрия была важным принципом композиции, широкое распростра­нение получила своеобразная игра в музыкальные голо­воломки. Одна из них заключалась в решении загадоч­ных «канонов». Канон — это одна из форм многоголос­ной музыки, основанной на проведении темы, которую ведет один голос, в других голосах. Композитор предла­гал какую-нибудь тему, а слушателям требовалось уга­дать операции симметрии, которые он намеревался ис­пользовать при повторении темы.

Природа задает головоломки как бы противополож­ного типа: нам предлагается завершенный канон, а мы должны отыскать правила и мотивы, лежащие в основе существующих узоров и симметрии, и наоборот, отыс­кивать узоры, возникающие при повторении мотива по разным правилам. Первый подход приводит к изучению структуры вещества, искусства, музыки, мышления. Вто­рой подход ставит нас перед проблемой замысла или пла­на, с древних времен волнующей художников, архитек­торов, музыкантов, ученых.

Винтовые повороты

Трансляцию можно комбинировать с отражением или поворотом, при этом возникают новые операции сим­метрии. Поворот на определенное число градусов, со­провождаемый трансляцией на расстояние вдоль оси поворота, порождает винтовую симметрию — симметрию вин­товой лестницы. Пример винтовой симметрии — распо­ложение листьев на стебле многих растений.

Головка подсолнечника имеет отростки, расположен­ные по геометрическим спиралям, раскручивающимся от центра наружу. Самые молодые члены спирали находят­ся в центре.

В таких системах можно заметить два семейства спи­ралей, раскручивающихся в противоположные стороны и пересекающихся под углами, близкими к прямым. Но какими бы интересными и привлекательными ни были проявления симметрии в мире растений, там еще много тайн, управляющих процессами развития.

Вслед за Гете, который говорил о стремлении приро­ды к спирали, можно предположить, что движение это осуществляется по логарифмической спирали, начиная всякий раз с центральной, неподвижной точки и сочетая поступательное движение (растяжение) с поворотом вра­щения.

Можно выделить также следующие виды симметрии Радиально-лучевая и билатеральнаясимметрия, встречающиеся в природе.

Симметрия подобия

Рассмотрим игрушечную матрешку, цветок розы или кочан капусты. Важную роль в геометрии всех этих при­родных тел играет подобие их сходных частей. Такие ча­сти, конечно, связаны между собой каким-то общим, еще не известным нам геометрическим законом, позволяю­щим выводить их друг из друга.

К перечисленным выше операциям симметрии мож­но, таким образом, добавить операцию симметрии подо­бия, представляющую собой своеобразные аналогии транс­ляций, отражений в плоскостях, повороты вокруг осей с той только разницей, что они связаны с одновременным увеличением или уменьшением подобных частей фигу­ры и расстояний между ними.

Симметрия подобия, осуществляющаяся в простран­стве и во времени, повсеместно проявляется в природе на всем, что растет. А ведь именно к растущим формам относятся бесчисленные фигуры растений, животных и кристаллов. Форма древесного ствола — коническая, силь­но вытянутая. Ветви обычно располагаются вокруг ство­ла по винтовой линии. Это не простая винтовая линия: она постепенно суживается к вершине. Да и сами ветви уменьшаются по мере приближения к вершине дерева. Следовательно, здесь мы имеем дело с винтовой осью сим­метрии подобия.

Живая природа в любых ее проявлениях обнаружива­ет одну и ту же цель, один и тот же смысл жизни: всякий живой предмет повторяет себя в себе подобном. Главной задачей жизни является ЖИЗНЬ, а доступная форма бы­тия заключается в существовании отдельных целостных организмов. И не только примитивные организации, но и сложные космические системы, такие как человек, де­монстрируют поразительную способность буквально по­вторять из поколения в поколение одни и те же формы, одни и те же скульптуры, черты характера, те же жесты, манеры.

Какое из чудес могло бы с большей силой поразить человеческое воображение, чем появление новой жиз­ни? Пространство, которое было ничем, становится де­ревом, яблоком, человеком. Возникновение живого су­щества — явление целостное, это таинство, так как чело­век не умеет познавать неделимое, не расчленяя его.

Природа обнаруживает подобие как свою глобальную ге­нетическую программу. Ключ в изменении тоже заключа­ется в подобии. Подобие правит живой природой в це­лом. Геометрическое подобие — общий принцип простран­ственной организации живых структур. Лист клена подобен листу клена, березы — березе. Геометрическое подобие пронизывает все ветви древа жизни.

Какие бы метаморфозы ни претерпевала в процессе роста в дальнейшем живая клетка, принадлежащая це­лостному организму и выполняющая функцию его вос­произведения в новый, особенный, единичный объект бытия, она является точкой «начала», которая в итоге деления окажется преобразована в объект, подобный пер­воначальному. Этим объединяются все виды живых струк­тур, по этой причине и существуют стереотипы жизни: человек, кошка, стрекоза, дождевой червь. Они беско­нечно интерпретируются и варьируются механизмами деления, но остаются теми же стереотипами организа­ции, формы и поведения.

Так же, как подобны одно другому целостные живые существа данного вида жизни, встроенные в ее непре­рывно разветвляющуюся цепь, так же подобны одно дру­гому и отдельные их члены, функционально специали­зированные.

Можно даже выделить, что функция зрения в целом, как и детальная структура органов зрительного восприя­тия, подчинена глобальному принципу организации жиз­ни — принципу геометрического подобия.

Определяя пространственную организацию живых организмов, прямой угол, который, кстати, правит физи­ческими процессами, организует жизнь силами гравита­ции. Биосфера (пласт бытия живых существ) ортогональ-на вертикальной линии земного тяготения. Вертикаль­ные стебли растений, стволы деревьев, горизонтальные поверхности водных пространств и в целом земная кора составляют прямой угол. Прямой гол является объектив­ной реальностью зрительного восприятия: выделение прямого угла осуществляют структуры сетчатки в цепи нейронных связей. Зрение чутко реагирует на кривизну прямых линий, отклонения от вертикальности и гори­зонтальности. Прямой угол, лежащий в основе треуголь­ника, правит пространством симметрии подобий, а по­добие, как уже говорилось, — есть цель жизни. И сама природа и первородная часть человека находятся во вла­сти геометрии, подчинены симметрии и как сущности и как символы. Как бы ни были выстроены объекты природы, каждый имеет свой основной признак, кото­рый отображен формой, будь то яблоко, зерно ржи или человек.

2. Разновидность симметрии и асимметрии в природе - свойства материального мира. Понятие симметрии и асимметрии в биологии.

Симметрия в природе

Внимательно приглядевшись к обступающей нас при­роде, можно увидеть общее даже в самых незначитель­ных вещах и деталях. Форма листа дерева не является случайной: она строго закономерна. Листок как бы скле­ен из двух более или менее одинаковых половинок, одна из которых расположена зеркально относительно другой. Симметрия листка упорно повторяется, будь то гусени­ца, бабочка, жучок и т. п.

Радиальнотлучевой симметрией обладают цветы, гри­бы, деревья, фонтаны. Здесь можно отметить, что на не сорванных цветах и грибах, растущих деревьях, бьющем фонтане или столбе паров плоскости симметрии ориен­тированы всегда вертикально.

Таким образом, можно сформулировать в несколько упрощенном и схематизированном виде общий закон, ярко и повсеместно проявляющийся в природе: все, что рас­тет или движется по вертикали, т. е. вверх или вниз отно­сительно земной поверхности, подчиняется радиально-лучевой симметрии в виде веера пересекающихся плоскостей симметрии. Все то, что растет и движется горизонтально или наклонно по отношению к земной поверхности, под­чиняется билатеральной симметрии, симметрии листка. Этому всеобщему закону подчиняются не только цве­ты, животные, легкоподвижные жидкости и газы, но и твердые, неподатливые камни. Этот закон влияет на из­менчивые формы облаков. В безветренный день они име­ют куполовидную форму с более или менее ясно выра­женной радиально-лучевой симметрией.

Влияние универсального закона симметрии являет­ся по сути дела чисто внешним, грубым, налагающим свою печать только на наружную форму природных тел. Внутреннее их строение и детали ускользают из-под его власти.

Асимметрия в живой природе

Молекулярная асимметрия была обнаружена и открыта Л. Пастером, которому удалось выделить левые и правые кристаллы винной кислоты. Асимметрия кристаллов квар­ца—в его оптической активности. В отличие от молекул неживой природы молекулы органических веществ име­ют ярко выраженный асимметричный характер.

Если считать, что равновесие характеризуется состо­янием покоя и симметрии, а асимметрия связана с дви­жением и неравновесным состоянием, то понятие рав­новесия играет в биологии не менее важную роль, чем в физике. Всеобщий закон биологии — принцип устойчиво­го термодинамического равновесия живых систем, опре­деляет специфику биологической формы движения ма­терии. Действительно, устойчивое термодинамическое равновесие (асимметрия) является основным принци­пом, который не только охватывает все уровни позна­ния живого, но и выступает в качестве ключевого прин­ципа постановки и решения происхождения жизни на земле.

Понятие равновесия может быть рассмотрено не толь­ко в статическом аспекте, но и в динамическом. Сим­метричной считается среда, находящаяся в состоянии термодинамического равновесия, среда с высокой энтропией и максимальным беспорядком частиц. Асиммет­ричная среда характеризуется нарушением термодинами­ческого равновесия, низкой энтропией и высокой упо­рядоченностью структуры.

При рассмотрении целостного объекта картина ме­няется. Симметричные системы, например кристаллы, характеризуются состоянием равновесия и упорядочен­ности. Но асимметричные системы, которыми являются живые тела, также характеризуются равновесием и упо­рядоченностью с тем только различием, что в последнем случае имеем дело с динамической системой.

Таким образом, устойчивое термодинамическое рав­новесие (или асимметрия) статической системы есть дру­гая форма выражения устойчивого динамического равновесия, высокой упорядоченности и структурности орга­низма на всех его уровнях. Такие системы называются асимметричными динамическими системами. Здесь нужно только указать, что структурность носит динамический характер.

Понятие равновесия тоже не является только стати­ческим, имеется и динамический аспект. Состояние сим­метрии и движения не есть нарушение равновесия вооб­ще, а есть состояние динамического равновесия. Здесь можно говорить о мере симметрии вообще, подобно тому, как в физике оперируют понятием движения.

Виды симметрии

Центральная симметрия

Центральная симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно центра О.

Если фигура при повороте плоскости вокруг некоторой точки самосов мещается за полный оборот не менее двух раз, то говорят, что она обладает симметрией относительно этой точки.

Количество самосовмещений фигуры за полный оборот называет порядком симметрии относительно точки.

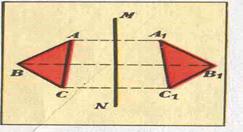
Две точки А и А₁ называются симметричными относительно точки О, если О - середина отрезка АА₁. Точка О считается симметричной самой себе.

Симметрия относительно точки

На рисунке точки М и М₁, N и N₁ симметричны относительно точки О, а точки Р и Q не симметричны относительно этой точки.

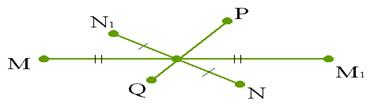
Фигура называется симметричной относительно точки О

если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией.

Простейшими фигурами, обладающими центральной симметрией, является окружность и параллелограмм.

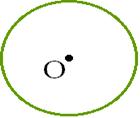
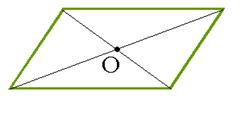
Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма точка пересечения его диагоналей.

Осевая симметрия

Осевая симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно оси а.

Две точки А и А₁ называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА₁ и перпендикулярна к нему.

Каждая точка прямой а считается симметричной самой себе.

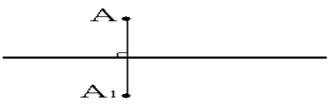
Симметрия относительно прямой

если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии фигуры.

Говорят также, что фигура обладает осевой симметрией.

У неразвёрнутого угла одна ось симметрии - прямая, на которой расположена биссектриса угла

Равнобедренный(но не равносторонний) треугольник имеет также одну ось симметрии, а равносторонний треугольник - три основные симметрии.

Прямоугольник и ромб, не являющиеся квадратами имеют по две оси симметрии, а квадрат - четыре оси симметрии.

У окружности их бесконечно много - любая прямая, проходящая через её центр, является осью симметрии.

Имеются фигуры, у которых нет ни одной оси симметрии. К таким фигурам относятся параллелограмм, отличный от прямоугольника, разносторонний треугольник.

Зеркальная симметрия

Что может быть больше похоже на мою руку или мое ухо , чем их собственное отражение в зеркале ? И все же руку которую я вижу в зеркале , нельзя поставить на место настоящей руки.

Иммануил Кант

Если каждая из половинок объекта является зеркальным отражением другой, относительно разделяющей их воображаемой плоскости, то говорят, что объект обладает зеркальной симметрии.

Зеркальная симметрия отображение пространства на себя, при котором любая точка переходит в симметричную ей точку, относительно плоскости а.

Поворотная симметрия

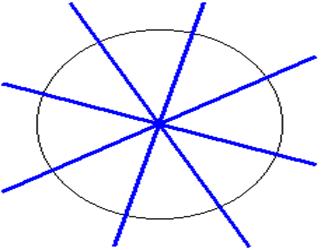
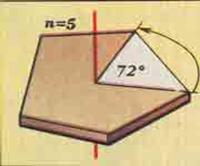
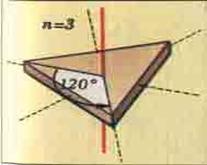
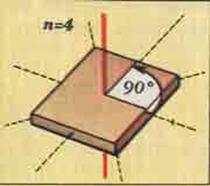
Поворотная симметрия - это такая симметрия при которой объект совмещается сам с собой при повороте вокруг некоторой оси на угол, равный 360°/n, где n = градусной мерой угла.

Если объект при вращении вокруг некоторой прямой самосовмещается за полный оборот не менее двух раз, то говорят, что он обладает поворотной симметрией. Прямую, вокруг которой объект вращается, называют поворотной осью, а количество самосовмещений объекта за полный оборот – порядком поворотной оси.

Принципы симметрии и асимметрии

НОУ ВПО Дальневосточный институт международного бизнеса

Факультет «Экономика и международный бизнес»

КОНТРОЛЬНАЯ РАБОТА

По «Концепциям современного естествознания»

ТЕМА: «Принципы симметрии и асимметрии»

Выполнила: студентка гр. 319 - БУ

Костина Е. А.

Шифр 09-БУ-08

Проверил (а): к. с. н., доцент

Зяблова Е. Ю.

Хабаровск 2009

ПЛАН РАБОТЫ

Введение 3

1. Симметрия как эстетический критерий. Операции и виды симметрии. Принципы симметрии. 5

2. Разновидность симметрии и асимметрии в природе - свойства материального мира. Понятие симметрии и асимметрии в биологии. 13

3. Золотое сечение – закон проявления гармонии природы. 26

Заключение 31

Список литературы

Введение

Первоначальный смысл симметрии – это соразмерность, сходство, подобие, порядок, ритм, согласование частей в целостной структуре. Симметрия и структура неразрывно связаны. Если некоторая система имеет структуру, то она обязательно имеет и некоторую симметрию. Идея симметрии имеет исключительное значение и как ведущее начало в осмыслении структуры естественнонаучного знания. Едва ли можно оспаривать эвристическую ценность и методологическое значение принципа симметрии. Известно, что при решении конкретных научных проблем этот принцип играет роль критерия истинности.

Симметрия является одной из наиболее фундаментальных и одной из наиболее общих закономерностей мироздания: неживой, живой природы и общества. С симметрией мы встречаемся всюду. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого знания; его широко используют все без исключения направления современной науки.

Что же такое симметрия? Почему симметрия буквально пронизывает весь окружающий нас мир? Существуют, в принципе, две группы симметрий.

К первой группе относится симметрия положений, форм, структур. Это та симметрия, которую можно непосредственно видеть. Она может быть названа геометрической симметрией.

Вторая группа характеризует симметрию физических явлений и законов природы. Эта симметрия лежит в самой основе естественнонаучной картины мира: ее можно назвать физической симметрией.

На протяжении тысячелетий в ходе общественной практики и познания законов объективной действительности человечество накопило многочисленные данные, свидетельствующие о наличии в окружающем мире двух тенденций: с одной стороны, к строгой упорядоченности, гармонии, а с другой - к их нарушению. Люди давно обратили внимание на правильность формы кристаллов, цветов, пчелиных сот и других естественных объектов и воспроизводили эту пропорциональность в произведениях искусства, в создаваемых ими предметах, через понятие симметрии.

«Симметрия, - пишет известный ученый Дж. Ньюмен, - устанавливает забавное и удивительное родство между предметами, явлениями и теориями, внешне, казалось бы, ничем не связанными: земным магнетизмом, женской вуалью, поляризованным светом, естественным отбором, теорией групп, инвариантами и преобразованиями, рабочими привычками пчел в улье, строением пространства, рисунками ваз, квантовой физикой, лепестками цветов, интерференционной картиной рентгеновских лучей, делением клеток морских ежей, равновесными конфигурациями кристаллов, романскими соборами, снежинками, музыкой, теорией относительности...".

1. Симметрия как эстетический критерий. Операции и виды симметрии. Принципы симметрии.

Одним из косвенных результатов СТО Эйнштейна явилась доказанная ею необходимость анализа, казалось бы, хорошо известных понятий, которые многие поко­ления воспринимали как нечто привычное, не требую­щее разъяснения.

В этом плане историю науки можно представить как историю попыток уточнения содержания и области при­менения научных понятий. И здесь успех всегда сопут­ствовал понятиям, которые выделялись своей эстетиче­ской привлекательностью. К таким понятиям может быть отнесена симметрия, которая с древнейших времен фигу­рировала в качестве скорее эстетического критерия, чем строго научного понятия.

Симметрия (от греч. symmetria - соразмерность) ­однородность, пропорциональность, гармония, инвари­антность структуры материального объекта относитель­но его преобразований. Это признак полноты и совер­шенства. Лишившись элементов симметрии, предмет ут­рачивает свое совершенство и красоту, т. е. эстетическое понятие.

Эстетическая окрашенность симметрии в наиболее общем понимании - это согласованность или уравнове­шенность отдельных частей объекта, объединенных в еди­ное целое, гармония пропорций. Многие народы с древ­нейших времен владели представлениями о симметрии в широком смысле как эквивалентности уравновешеннос­ти и гармонии. В геометрических орнаментах всех веков запечатлены неиссякаемая фантазия и изобретательность художников и мастеров. Их творчество было ограничено жесткими рамками, требованиями неукоснительно сле­довать принципам симметрии. Трактуемые несравненно шире, идеи симметрии нередко можно обнаружить в живописи, скульптуре, музыке, поэзии. Операции сим­метрии часто служат канонами, которым подчиняются балетные па: именно симметричные движения составля­ют основу танца. Во многих случаях именно язык сим­метрии оказывается наиболее пригодным для обсужде­ния произведений изобразительного искусства, даже если они отличаются отклонениями от симметрии или их со­здатели стремятся умышленно ее избежать.

Можно выде­лить следующие операции симметрии:

■ отражение в плоскости симметрии (отражение в зер­кале);

■ поворот вокруг оси симметрии (поворотная симметрия);

■ отражение в центре симметрии (инверсия);

■ перенос (трансляция) фигуры на расстояние;

■ винтовые повороты.

Отражение в плоскости симметрии

Отражение — это наиболее известная и чаще других встречающаяся в природе разновидность симметрии. Зеркало в точности воспроизводит то, что оно «видит», но рассмотренный порядок является обращенным: правая рука у вашего двойника в действительности окажется ле­вой, так как пальцы расположены на ней в обратном порядке. Всем, наверное, с детства знаком фильм «Ко­ролевство кривых зеркал», где имена всех героев чита­лись в обратном порядке.

Зеркальную симметрию можно обнаружить повсюду: в листьях и цветах растений, архитектуре, орнаментах. Че­ловеческое тело, если говорить лишь о наружном виде, обладает зеркальной симметрией, хотя и не вполне стро­гой. Более того, зеркальная симметрия свойственна телам почти всех живых существ, и такое совпадение отнюдь не случайно. Важность понятия зеркальной симметрии вряд ли можно переоценить.

Зеркальной симметрией обладает все, допускающее разбиение на две зеркально равные половинки. Каждая из половинок служит зеркальным отражением другой, а разделяющая их плоскость называется плоскостью зер­кального отражения, или просто зеркальной плоскостью. Эту плоскость можно назвать элементом симметрии, а со­ответствующую операцию — операцией симметрии.

Отражение в зеркале — это один из способов повто­рения фигуры, приводящий к возникновению симмет­ричного узора. Если использовать не одно, а два зеркала, то можно получить устройство, названное калейдоско­пом, открытое в 1819 г. Д. Брюстером. В калейдоскопе совмещаются два вида симметрии: зеркальная и пово­ротная. Расположив зеркала под определенным углом, можно увидеть отражение, отражение отражения и т. д. Вечно изменяющаяся череда узоров завораживает взор каждого.

Если два зеркала не пересекаются, а установлены па­раллельно друг другу, то вместо орнамента с элемента­ми, расположенными по кругу, получается бесконечный узор, который повторяется и напоминает бордюр или ленту из ткани.

С трехмерными симметричными узорами мы сталки­ваемся ежедневно: это многие современные жилые зда­ния, а иногда и целые кварталы, ящики и коробки, гро­моздящиеся на складах, атомы вещества в кристалличес­ком состоянии образуют кристаллическую решетку — элемент трехмерной симметрии. Во всех этих случаях правильное расположение позволяет экономно исполь­зовать пространство и обеспечивать устойчивость.

Поворотная симметрия

Внешний вид узора не изменится, если его повернуть на некоторый угол вокруг оси. Симметрия, возникающая при этом, называется поворотной симметрией. Примером может служить детская игра «вертушка» с поворотной сим­метрией. Во многих танцах фигуры основаны на враща­тельных движениях, нередко совершаемых только в одну сторону (т. е. без отражения), например, хороводы.

Листья и цветы многих растений обнаруживают ра­диальную симметрию. Это такая симметрия, при которой лист или цветок, поворачиваясь вокруг оси симметрии, переходит в себя. На поперечных сечениях тканей, обра­зующих корень или стебель растения, отчетливо бывает видна радиальная симметрия. Соцветия многих цветков также обладают радиальной симметрией.

Отражение в центре симметрии

Примером объекта наивысшей симметрии, характе­ризующим эту операцию симметрии, является шар. Ша­ровые формы распространены в природе достаточно ши­роко. Они обычны в атмосфере (капли тумана, облака), гидросфере (различные микроорганизмы), литосфере и космосе. Шаровую форму имеют споры и пыльца расте­ний, капли воды, выпущенной в состоянии невесомости на космическом корабле. На метагалактическом уровне наиболее крупными шаровыми структурами являются галактики шаровой форм