Для искусственного интеллекта

ЯЗЫКИ И ТЕХНОЛОГИИ ПРОГРАММИРОВАНИЯ

ДЛЯ ИСКУССТВЕННОГО ИНТЕЛЛЕКТА

Языки программирования LISP и PROLOG чаще всего применяются для решения задач искусственного интеллекта. Их синтаксис и семантика дают богатый материал для рассуждения о задачах и их решениях. Во многом это определяется их мощностью, а также возможностью их рассмотрения как "средства мышления".

8.1. Обзор языка PROLOG

PROLOG – это наиболее известный пример языка логического программирования (logic programming language). Логическая программа – это набор спецификаций в рамках формальной логики. PROLOG основан на теории предикатов первого порядка. Само имя этого языка расшифровывается как Programming in Logic (Программирование в логике). При выполнении программы интерпретатор постоянно реализует вывод на основе логических спецификаций. Идея использования возможностей представления теории предикатов первого порядка – это одно из основных преимуществ применения языка PROLOG для компьютерных наук вообще, и компьютерного интеллекта в частности.

Развитие языка PROLOG уходит корнями в исследования, связанные с доказательством теорем, а точнее, с разработкой алгоритмов опровержения резолюции. Процедура доказательства, получившая название резолюции (resolution), стала основным методом вычислений на языке PROLOG. Частично метод резолюции описан в п. 2.2.3.

Благодаря этим свойствам PROLOG зарекомендовал себя в качестве полезного средства исследования таких экспериментальных вопросов программирования, как автоматическая генерация кода, верификация программ и разработка высокоуровневых языков программирования. PROLOG, как и другие основанные на логике языки, поддерживает декларативный (описательный) стиль программирования, то есть конструирование программ в терминах точного определения ситуации и точной формулировки задачи. В отличие от него процедурный язык программирования предполагает написание программы в виде последовательности инструкций по выполнению алгоритма. В логическом программировании компьютеру сообщается, "что есть истина", а не "как решить задачу". Это позволяет программисту сосредоточиться на решении задачи и создании описаний для предметной области, а не на деталях описания низкоуровневых алгоритмических конструкций вида "что делать далее".

Первая PROLOG-программа была написана в начале 1970 годов во Франции в рамках проекта по пониманию естественного языка [49]. Теоретические основы этого языка описаны в работах Р. Ковальски [49, 50]. Основной этап развития языка PROLOG приходится на 1975–1979 годы, когда на кафедре искусственного интеллекта университета Эдинбурга Дэвид Уоррен и Фернандо Перейра отвечали за реализацию этого языка. Они создали первый интерпретатор PROLOG. Описание этого кода и результаты сравнения PROLOG с языком LISP приводятся в книге Д. Варена [62]. Эта версия стала первым стандартом языка и была описана в книге У. Клоксина и М. Меллиша [38]. Русский перевод этой книги вышел в 1987 году [18].

В настоящее время наиболее популярна созданная в 1986 году система Turbo-Prolog, работающая под MS DOS, и система VISUAL-PROLOG под WINDOWS.

8.2. Типы данных PROLOG

Предложим классификацию данных PROLOG как на рис. 8.1.

Переменные - это данные PROLOG, имеющие имя, представляющее собой набор букв и цифр, начинающийся с заглавной (прописной) буквы. Переменная может быть конкретизирована каким-либо значением или не конкретизирована. Следует отметить, что конкретизация не является полным аналогом оператора присваивания.

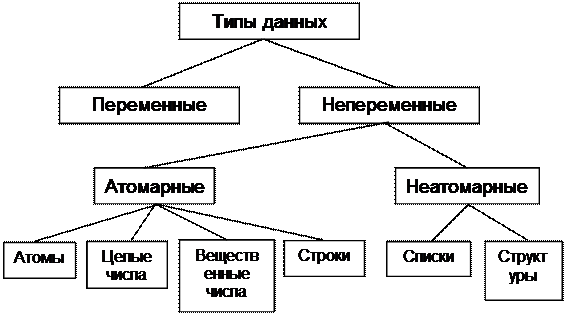Рис. 8.1. Классификация данных PROLOG

Переменная получает свое значение только в результате сопоставления с константами в фактах и правилах программы. Получив значение, переменная владеет им лишь до получения ответа на запрос. После этого переменная вновь становится свободной и участвует в поиске альтернативных решений. Поэтому следует помнить:

- переменная не является хранилищем информации на все время работы программы, а служит частью процесса сопоставления (унификации), о котором речь пойдет далее;

- областью действия переменной является не вся программа, а лишь одно предложение, то есть одно правило или один вопрос.

Во многих случаях переменная встречается в правиле только один раз и ее значение не влияет на результат логического вывода. Такую переменную называют анонимной и замещают знаком подчеркивания.

Атомом называют любой набор символов алфавита, заключенный в кавычки, или набор строчных букв и цифр, начинающийся с буквы, например:

"alpha","Alpha","4beta",anna,x5

Не являются атомами наборы:

1b,#d,a-b

Атомом также является любой символ алфавита. Например:

( , ; , < , >

Числовые константы определяются в PROLOG так же, как и в других языках.

Принято также использовать рекурсивное определение списка:

- пустой список [] – это список;

- [A¦B] – список, если B – список.

И наконец, структурой называют единый объект PROLOG, состоящий из совокупности других объектов, например:

Отец(Х,иван)

8.3. Структура программы на PROLOG

Программа на языке PROLOG состоит из:

- раздела объявления типов переменных (domains);

- раздела объявления предикатов (predicates);

- раздела целей (clauses).

Раздел объявления типов переменных имеет вид:

Domains

<список имен типов>=<описание типа>.

Например:

Domains

X=integer.

Z=real.

U=symbol*.

В этом разделе объявлены целый тип с именем X, вещественный тип с именем Z, и тип U обозначает список слов.

Раздел объявления предикатов имеет вид:

Predicates

<имя предиката>(<список типов аргументов>).

Например:

Predicates

vvod(X).

dlina(U,X).

Здесь объявлен предикат vvod с одним целым аргументом, и предикат dlina с двумя аргументами, первый из которых – список, второй – целое число.

В конце любого предложения ставится точка.

8.3.1. Раздел целей

Фактом называют предложение PROLOG следующего вида:

<имя факта>(<список констант через запятую>), –

которое считается всегда истинным.

Например:

Хобби(анна,марки).

Хобби(петя,фантики).

Данное([1,2,3,4]).

Предикатом называют предложение PROLOG вида:

<имя предиката>(<список имен переменных и констант через запятую>),

которое может принимать значение истина или ложь в зависимости от значений переменных.

Правилом называют следующее предложение PROLOG:

<предикат> if <предикат1>, <предикат2>, ...,<предикатN>.

Раздел целей PROLOG имеет вид:

Clauses

<факты>.

<правила>.

Например:

Clauses

Отец(Иван,Петр). /*Иван–отец Петра*/

Отец(Иван,Игорь). /*Иван – отец Игоря*/

Отец(Игорь,Семен).

Отец(Игорь,Анна).

Дед(X,Y) if отец(Z,Y),отец(X,Z).

/*X–дед Y,если отцом Y является Z, а отцом

Z является Х*/

8.3.2. Организация запросов на PROLOG

Последним элементом программы на PROLOG являются вопросы. Вопросы можно сформулировать в теле программы в разделе GOAL, который вводится после раздела Clauses.

Например:

GOAL

дед(Х,анна) /*кто дед анны?*/

Сформулированный так запрос называется внутренней целью.

Но можно формулировать вопрос после нажатия <Run> в открывающемся при этом окне <goal>

goal:дед(Х,анна).

В этом случае цель называется внешней.

Пример

8.1. Построить базу знаний из следующих фактов: Карл у Клары украл кораллы. Клара у Карла украла кларнет.

Построить вопросы: Кто украл кларнет? Кто украл кораллы? Что украл Карл? Что было украдено?

Решение:

domains

X,Y,Z=symbol.

predicates

украл(X,X,X).

clauses

украл(карл,кораллы,клара).

украл(клара,кларнет,карл).

/*вопросы могут быть заданы так:*/

goal:украл(Х,кларнет,Y)

ответ:Х=клара Y=карл

goal украл(Х,кораллы,Y).

ответ:Х=карл Y=клара

goal украл(карл,Х,Y)

ответ:Х=кораллы Y=клара

goal украл (X,Y,Z)

ответ:Х=карл Y=кораллы Z=клара

Х=клара Y=кларнет Z=карл

Упражнения

8.1. Построить базу данных своих родных мужского пола с фактами: отец и сын – и правилами: дед, внук, брат.

8.2. Построить базу данных: отец, сын, дядя, племянник, дед, внучатый
племянник.

8.3. Построить базу знаний «студент» с полями: фамилия, балл 1, балл 2 – и правило "стипендия" с полями: фамилия, сумма.

8.4. Построить базу данных о родственниках: мать – дочь и правила: тетя, племянница, бабушка, внучатая племянница.

8.5. Построить базу данных «телефонная книга» с полями: фамилия, номер, адрес – и правила.

8.6. Построить базу данных «родитель» (имя родителя, имя ребенка) и правила: мать, отец.

8.7. Построить базу данных фактов: мальчик (имя), девочка (имя), дружит (имя, имя) – и правила: приятели (Х, Y), приятельницы (Х, Y).

8.8. Построить базу данных из фактов, кто на чем играет (имя, инструмент) и правило "квартет" (X, Y, Z, T).

8.9. Построить базу данных из фактов: мужчина (имя, возраст), женщина (имя, возраст) – и правило "подлежит призыву" (имя).

8.10. Построить базу данных из фактов: ученик (фамилия, класс, школа), – правило "одноклассники" (X, Y).

8.11. Построить базу данных «знакомства» из следующих фактов и правил: Мери прелестна; Джон добрый; Джон мужественный; Джон сильный, некто счастлив, если богат и нравится женщинам; мужчина нравится женщине, если женщина нравится мужчине и он добрый, либо мужчина добрый и сильный; мужчине нравится женщина, если она прелестна.

8.4. Ввод-вывод данных на PROLOG

Для организации ввода используются стандартные предикаты readint(X), readreal(X), readchar(X), …, позволяющие ввести соответственно целое, вещественное число, одну литеру или строку символов.

Для вывода данных на экран служат стандартные предикаты: write(X) и nl - перевод курсора на новую строку.

Пример

8.2. Закончим раздел примером вычисления суммы двух введенных с клавиатуры целых чисел.

domains

X,Y,Z=integer.

predicates

vvod(X,X).

sum(X,X,X).

clauses

vvod(X,Y) if write(«введите Х, Y»),

readint(X),readint (Y).

sum(X,Y,Z) if vvod(X,Y),Z=X+Y.

goal:sum(X,Y,Z).

Система выведет на экран приглашение к вводу, дождется ввода с клавиатуры двух чисел и выведет полученное значение Z.

8.5. Разветвления на PROLOG

Пролог не содержит инструкций, аналогичных инструкциям разветвления и повторения в процедурных языках. Реализация этих процессов происходит в соответствии с правилами логического вывода. Поэтому для программирования нескольких реализаций одного и того же предиката следует построить столько же правил, сколько ветвей у предиката. Причем у всех ветвей головой правил служит изучаемый предикат.

предикат if <первая ветвь разветвления>.

предикат if <вторая ветвь разветвления>.

- - - - - - - - - - - - - - - - - - - - - -

предикат if <последняя ветвь разветвления>

Пример

8.3. Для примера рассмотрим программу определения типа образовательного учреждения, которое посещает ребенок в зависимости от его возраста.

Domains

X,Y=symbol.

Predicates

ввод(X).

вывод(X).

посещает(X,X)

ответ.

Clauses

Ввод(X) if write(“введите возраст ребенка”),readint(X),nl.

Вывод(Y) if write(”ребенок посещает”),write(Y).

Посещает(X,Y) if X<3,Y=”ясли”.

Посещает(X,Y)if X>=3,X<=6,Y=.”дет.сад”.

Посещает(X,Y) if X>6,Y=.”школа”.

Ответ if ввод(X),посещает(X,Y),вывод(У).

Упражнения

8.12. Найти большее из двух чисел.

8.13. Найти меньшее из трех чисел.

8.14. Вывести на экран название угла в зависимости от его величины (острый, тупой, прямой, развернутый).

8.15. Даны длины трех отрезков. Могут ли эти отрезки служить сторонами треугольника?

8.16. Ввести результаты двух экзаменов и вывести размер стипендии.

8.17. Вычислить значение функции 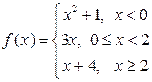при заданном х.

8.18. Найти абсолютную величину заданного числа.

8.19. Найти значение функции 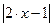при заданном х.

8.20. Найти значение функции max(a,c)+max(b,c,d)при заданных a,b,c,d.

8.21. Найти значение функции |x+xy+1| при заданных х,y.

8.22. Найти значение функции max(a,b,c)–min(b,c) при заданных a,b,c.

8.23. Найти значение функции min(a,b)+min(b,c,d)при заданных a,b,c,d.

8.24. Найти значение функции |2x + y| при заданных х,y.

8.25. Найти значение функции max (a, b) – max (a, c, d) при заданных a, b, c, d.

8.26. Найти значение функции |3a – b| при заданных a, b.

8.27. Найти значение функции max (a, c) + max (b, c, d) при заданных a, b, c, d.

8.28. Найти значение функции | x + xy + 1| при заданных х, y.

8.29. Найти значение функции max (a, b, c) – min (b, c) при заданных a, b, c.

8.30. Найти значение функции |ab – 1| при заданных a, b.

8.31. Найти значение функции min (a, b) + min (b, c, d) при заданных a, b, c, d.

8.32. Найти значение функции |x – y²| при заданных х, y.

8.33. Найти значение функции max (a, b) – min (a, b, c) при заданных a, b, c.

8.34. Найти значение функции |x² – y| при заданных х, y.

8.35. Найти значение функции min (a, c) – min (b, c) при заданных a, b, c.

8.36. Найти значение функции |x² – y²| при заданных х, y.

8.37. Найти значение функции min (a, b) × min (a, c) при заданных a, b, c.

8.38. Найти значение функции |3x + y| при заданных х, y.

8.39. Найти значение функции max (a, b) + min (a, c) при заданных a, b, c.

8.40. Найти значение функции |6x – y| при заданных х, y.

8.41. Найти значение функции min (a, b) + min (d, c) при заданных a, b, c, d.

8.42. Найти значение функции |x – 8y²| при заданных х, y.

8.43. Найти значение функции max (a, c) × min (d, l) при заданных a, c, d.

8.44. Найти значение функции |2x – 3y| при заданных х, y.

8.45. Найти значение функции 2 min (a, b, c) при заданных a, b, c.

8.46. Найти значение функции |ab + c| при заданных a, b, c.

8.47. Найти значение функции max (a, c) – min (a, c) при заданных a, c.

8.48. Найти значение функции |ac – b| при заданных a, b, c.

8.49. Найти значение функции min (a, c) × min (d, e) при заданных a, c, d, e.

8.50. Найти значение функции |a² – ac| при заданных a, c.

8.51. Найти значение функции max (a, b) + min (b, c) при заданных a, b, c.

8.52. Найти значение функции |x – y²| при заданных х, y.

8.53. Найти значение функции min (a, b, c) × max (a, b) при заданных a, b.

8.6. Правила логического вывода

8.6.1. Понятие об унификации и конкретизации

Унификацией называется отождествление объектов PROLOG при сопоставлении предиката с фактами и правилами базы данных. Если такое отождествление выполнено, то говорят, что унификация завершена успешно. При таком сопоставлении свободные переменные доказываемого предиката приобретают конкретные значения. Этот процесс называется конкретизацией.

Пример

8.4.Пусть имеется база знаний:

пишет("Петров",портреты).

пишет("Репин",картины).

пишет("Суриков",картины).

пишет("Блок",стихи).

пишет("Аксенов",романы).

художник(X)if пишет(Х,портреты).

художник(X)if пишет(Х,картины).

писатель(X)if пишет(Х,стихи).

писатель(X)if пишет(Х,романы).

Сделаем запрос: «Кто является писателем?»:

писатель(X).

Предикат писатель(X) сопоставляется с фактами базы знаний, после чего сопоставляется с головой правила писатель(Х). Поскольку сопоставление успешно, то переменная Х конкретизируется значением "Блок". Выполняется доказательство цели писатель (“Блок”). Для доказательства изучается первый предикат правой части правила пишет (“Блок”,стихи). Этот предикат сопоставляется с фактом базы данных. При сопоставлении с фактом пишет (“Блок”,стихи), унификация завершается успешно, то есть предикат пишет(“Блок”,стихи) принимает значение "истина", голова правила писатель(“Блок”) принимает значение "истина". При этом Х конкретизируется значением "Блок" на экране выдается сообщение "!да!".

8.6.2. Правило логического вывода на PROLOG

Характер логического вывода зависит от вида вопроса. Если вопрос не содержит переменных, а только константы, то такой вопрос называется общим и ответ на него будет «да» или «нет» в зависимости от результатов сопоставления с фактами и правилами программы. Если же вопрос содержит переменные, то в процессе сопоставления переменные будут конкретизированы и эти значения будут выведены на экран, в противном случае ответ будет «нет». Процесс доказательства правила:

предикат if предикат1,предикат2,… предикатn

можно описать следующим образом:

1. Выполняется сопоставление предикат1 с фактами и правилами базы данных. Если сопоставление невозможно, то голова правила - предикат - получает значение «ложь». Если нашелся вариант сопоставления, при котором предикат1 = истине, то переход к доказательству предикат2.

2. Выполняется доказательство предикат2 с теми параметрами, при которых был истинен предикат1. Если это возможно, то переход к доказательству предикат3. Если невозможно, то происходит одна из основных операций PROLOG - откат, то есть возврат к предикат1 и поиску других значений параметров предикат1, при которых он будет истинен. Если таковые найдутся, то выполняется возврат к предикат2 и производится попытка его доказательства для новых, альтернативных значений параметров предикат1. Этот процесс выполняется до тех пор, пока не будут просмотрены все варианты доказательства предикат2. Если при всех возможных вариантах предикат1 второй предикат принимает значение ложь, то задача считается решенной и голова правила получает значение ложь. Если найдется вариант предикат1, при котором предикат2 = истине, то происходит переход к доказательству предикат3 и так далее.

Упражнения

8.54. Создать БД "ученик" (имя, предмет, балл). Создать правила: хорошист, отличник, двоечник.

8.55. Создать БД "поезд" (пункт отправления, пункт назначения, время в пути, расстояние). Сделать правила: пригородный, дальний, дневной, ночной.

8.56. Создать БД "учитель" (предмет, фамилия, стаж, № школы) и правила: филолог, естественник, опытный, начинающий.

8.57. Создать БД "дядя-племянник" и "тетя-племянник". Создать правила: кузен, внучатый племянник.

8.58. Создать БД "автор" (имя, вид произведения, страна) и правила" писатель, композитор, европейский, азиатский.

8.59. Создать БД "тетя-племянница", "дядя-племянница" и правила: кузины, внучатые племянницы.

8.60. Написать БД "студент" (фамилия, балл 1, балл 2) и правило "стипендия" (имя, величина).

8.61. Написать БД "победа" (команда 1, команда 2) для 4 команд. Сделать правило "победитель" (команда 1, команда 2).

8.62. Создать БД "путь" (пункт 1, пункт 2) для 5 населенных пунктов и правило "есть путь" (A, B).

8.63. Создать БД "мать-дочь" и правило "прабабушка".

8.64. Создать БД "родитель-потомок". Сделать правила: сын, дочь.

8.65. Создать БД "жильцы" (фамилия, этаж, квартира) и правило "плата за лифт (X) для жильцов этажей выше 3".

8.66. Создать БД "мать-дочь" и "мать-сын". Создать правила: брат (X, Y) и сестра (X, Y).

8.67. Создать БД "отец-дочь" и "отец-сын" и правило "дедушка" (X, Y).

8.68. Создать БД: возраст (имя, возраст), мужчина (X), женщина (X) и правило "подлежит призыву (X)".

8.6.3. Задачи на упорядочение объектов

Пример

8.5. Рыбак поймал окуня, ерша и щуку. Щуку он поймал раньше окуня, ерша позже щуки, но раньше окуня. Какая рыба поймана раньше всех?

Clauses

Раньше(щука,окунь).

Раньше(щука,ерш).

Раньше(ерш,окунь).

Порядок(X,Y,Z) if раньше(X,Y),раньше(Y,Z).

Goal

Порядок(X,Y,Z).

Упражнения

8.69. Ира и Лена одинакового роста. Лена выше Оли, Таня выше Иры. Кто выше: Таня или Оля?

8.70. Даны 4 числа X, Y, Z, T. Известно, что Х меньше Y и меньше Т; Y больше Z и больше Т; Z больше Х и меньше Т. В каком порядке расположены числа?

8.71. Возле почты растут 6 деревьев: сосна, береза, липа, тополь, ель и клен. Какое дерево самое высокое и какое самое низкое, если известно, что береза ниже тополя, липа выше клена, сосна ниже ели, липа ниже березы, сосна выше тополя.

8.72. В очереди за билетами в кино стоят Юра, Миша, Володя, Саша и Олег. Известно, что Юра купил билет раньше Миши, но позже Олега; Володя и Олег не стояли рядом; Саша не находился рядом ни с Олегом, ни с Юрой, ни с Володей. Кто за кем стоит?

8.73. На улице, встав в кружок, беседуют 4 девочки: Аня, Валя, Галя, Надя. Девочка в зеленом платье - не Аня и не Валя - стоит между девочкой в голубом платье и Валей. Девочка в белом платье стоит между девочкой в розовом платье и Галей. Какого цвета платье у каждой девочки?

8.74. Трое юношей Коля, Петя, Юра влюблены без взаимности в трех девушек: Таню, Зину, Галю. Кто в кого влюблен, если Коля любит девушку, влюбленную в юношу, который любит Зину; Петя любит девушку, влюбленную в юношу, который любит Галю; Зина не любит Юру.

8.75. У меня три карандаша: желтый, синий, черный. Можно ли назвать самый короткий и самый длинный в следующих случаях:

а) черный короче желтого, желтый короче синего;

б) желтый длиннее черного, черный длиннее синего.

8.76. Составить базу знаний по сказке «Репка». Определить весь ряд персонажей, тянущих репку. Составить правила:

а) кто первый тянет репку;

б) кто тянет после бабки;

в) кто на 4 месте?

8.77. Воробей, дятел и синица сидели на одной ветке. В каком порядке они сидели, если:

а) синица сидела слева от дятла, а воробей слева от синицы;

б) дятел сидел слева от синицы и справа от воробья;

в) воробей сидел справа от синицы, а дятел справа от воробья.

8.78. Береза выше рябины, но ниже тополя. Кто выше: рябина или тополь. Какое дерево самое низкое?

8.79. Назовите имена мальчиков самого высокого, среднего и самого низкого, если

а) Вася ниже Коли, Коля ниже Толи;

б) Вася ниже Толи, Толя выше Коли.

8.80. О четырех числах X, Y, Z, T известно, что Y меньше Х и меньше Т, Х больше Z и больше T, Z больше Y и меньше T. Какое число самое маленькое и какое – самое большое.

8.7. Рекурсия на PROLOG

8.7.1. Понятие рекурсии на PROLOG

В предыдущем разделе мы рассмотрели организацию разветвления на PROLOG. Для программирования повторений на процедурных языках существует целая серия операторов цикла. PROLOG-система для этой цели использует совершенно иное, гораздо более мощное средство - рекурсию.

Рекурсией называется обращение структуры к самой себе. Слово «рекурсия» переводится как «обратное движение, возвращение». Используют рекурсию в следующих случаях:

а) для описания программ, выполнению которых предшествует выполнение их собственной копии;

б) для описания структур, имеющих другие структуры в качестве компонент.

С первым способом использования рекурсии хорошо знакомы все, кому приходилось программировать на процедурных языках высокого уровня. Второй способ реализован только в языках логического программирования и является естественным приемом представления структур данных. Остановимся на различных вариантах этого способа.

8.7.2. Числовая рекурсия

Хорошо известно правило вычисления n! через (n - 1)! При этом граничным условием или условием выхода из рекурсии является соглашение, что 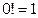. Таким образом, имеется рекурсивное правило: n! = (n – 1)! × n и граничное условие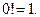

На PROLOG эти два допущения можно записать так:

fact(0,1)if!.

fact(N,X)if M=N-1,fact(M,Y),X=Y+N.

Зададим вопрос:

fact(3,X).

Процесс работы программы можно изобразить как на рис. 8.1.

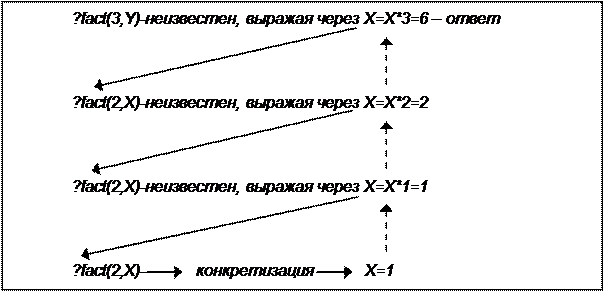
Рис. 8.1. Рекурсия

Здесь сплошная стрелка означает очередное сопоставление и его результат (резолюцию) при движении к граничному условию, а пунктирная - обратный ход рекурсии до получения ответа на заданный вопрос. В программе использован стандартный предикат "!", называемый "отсечение" (по английски "cut"). Он прекращает поиск альтернативных решений после достижения граничного условия. PROLOG-системе не известно, нужны ли программисту другие варианты ответа, система, если нет других указаний, всегда будет искать все возможные ответы и будет продолжать прямой ход для Х = -1, -2, … до исчерпания стека. Чтобы этого не случилось, в правой части граничного правила стоит предикат "!".

Приведем еще два примера числовой рекурсии.

Примеры

8.6.Найти 4 член в последовательности чисел Фибоначчи:

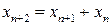, если 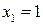, , 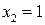где

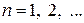
fib(1,.,1) if!./*определим 1-е число,0-е-не определено*/

fib(2,1,1) if!./*второе число=1,первое число=1*/

fib(N,X,Y) if M=N-1,fib(M,L,X),Y=L+X.

/*N-е число=Y, предыдущее N-1=X,

если M=N- 1, M–е число=Х, М-1-е число=L,

а Y=L+X*/.

8.7.Найти наибольший общий делитель NOD(M, N).

Clauses

Nod(X,X,X) if!.

Nod(X,Y,K) if X>Y,R=X-Y,nod(R,Y,K).

Nod(X,Y,K) if Y>X,R=Y-X,nod( X,Y,K).

/* если два числа X и Y равны, то nod=X, если не равны то уменьшать большее на величину меньшего до тех пор ,пока числа не сравняются*/.

8.8.Написать программу с внутренней целью, которая осуществляет ввод с клавиатуры и выводит значение x_n для:

x_n=x_n-1+2x_n-2, x₁=x₂=1, x₅=?

predicates

xn(integer,integer)

writeresult(integer)

query

clauses

xn(X,1) if X<=2,!.

xn(X,Y) if X1=X-1, xn(X1,Y1),X2=X-2, xn(X2,Y2),Y=Y1+2*Y2

writeresult(X) if

X<=0,

write("no solutions because N<=0"),

nl,!

writeresult(X) if

xn(X,Y),

write(Y),nl.

query if

write("input N: "), readint(N),

writeresult(N).

goal

query.

Упражнения

В следующих упражнениях написать программу с внутренней целью, которая осуществляет ввод с клавиатуры и выводит значение x_n .

8.81. x_n = 2x_n-1 – 1, x₁=1, x₅ = ?

8.82. x_n = n/x_n-1, x₁ = 2, x₅ = ?

8.83. x_n = 3x_n-1 + 1, x₁ = 2, x₅ = ?

8.84. x_n+1 = 2x_n – x_n-1, x₁ = 3, x₂ = 1, x₆ = ?

8.85. x_n = 1+x_n-1 + x_n-2, x₁ = x₂ = 2, x₆ = ?

8.86. x_n+1 = x_n + x_n-1 + 3, x₁ = 1, x₂ = 2, x₅ = ?

8.87. x_n+2 = x_n + 2x_n+1, x₁ = 2, x₂ = 1, x₆ = ?

8.88. x_n = x_n-1 + x_n-2 + 2, x₁ = x₂ = 1, x₆ = ?

8.89. x_n+2 = x_n + 1/x_n+1, x₁ = x₂ = 1, x₅ = ?

8.90. x_n+1 = x_n × x_n-1, x₁ = 1, x₂ = 1/2, x₆ = ?

8.91. x_n+2 = 2x_n+1 + 3x_n, x₁ = 0, x₂ = 1, x₅ = ?

8.92. x_n = x_n-1 + 2x_n-2, x₁ = x₂ = 1, x₅ = ?

8.93. x_n+2 = 2x_n+1 + x_n, x₁ = 2, x₂ = 1, x₅ = ?

8.94. x_n+2 = x_n+1 + x_n/2, x₁ = 1, x₂ = 2, x₅ = ?

8.95. x_n+1 = x_n + 2x_n-1, x₁ = x₂ = 1, x₆ = ?

8.7.3. Рекурсия в графике

Если в состав PROLOG-системы входит модуль GRAPH, то знакомиться с рекурсией удобно на примере простейших графических построений. Общее правило построения N рисунков можно сформулировать так:

· рекурсивное правило: чтобы нарисовать N рисунков, надо уметь нарисовать N - 1 рисунок и знать, как рисуется N-я картинка.

· граничное правило:надо знать, как рисуется первый рисунок.

Примеры

8.9.Изобразить на экране 20 точек, расположенных в одной строке на расстоянии 10 пикселей друг от друга. Первая точка имеет координаты (50, 50). Пусть граф-драйвер находится в текущем каталоге.

clauses

init if initgraph(0,0,_,_,” ”).

ris(1) if putpixel(50,50,15),!.

ris(N) if M=N-1,ris(M),X=50+20+M,putpixel (X, 50, 15).

rez if init,ris(20),readln(_),closegraph.

goal

rez.

8.10.Построить 15 концентрических окружностей с центром в точке (300, 200) с радиусами, отличающимися друг от друга на 10 пикселей. Внутренняя окружность имеет R = 10.

clauses

konz(1) if circle(300,200,10)!.

konz(N) if M=N-1,konz(M),R=10+M*10,

circle(300,200,R).

goal

initgraph(0,0,_,_,””),konz(15),readln(_),

closegraph.

8.11. Выполнить рисование каждой из окружностей случайно выбранным цветом.

clauses

zwet(c) if c=random(15),setcolor(c).

konz(1) if zwet(c),circle(300,200,10),!.

konz(N,c) if M=N-1,konz(M),zwet(c),k=10+M *10,circle(300,200,R).

goal

initgraph (0,0,_,_,””),konc(15,c).

8.12. Нарисовать 4 расположенные друг под другом окружности.

predicates

image_item (integer)

query

clauses

image_item (0) if !.

image_item (N) if

Y = N * 100 – 50,

circle (50, Y, 40),

M = N – 1,

image_item (M).

query if

initgraph (0, 0, _, _, ""),

cleardevice,

setcolor (15),

image_item (4),

readln (_),

closegraph.

goal

query.

Упражнения

Написать программу с внутренней целью, которая рисует в графическом режиме один из представленных ниже рисунков, используя рекурсивный вызов предиката, рисующего отдельные повторяющиеся части изображения:

8.96.

8.97.

8.98.

8.99.

8.100.

8.101.

8.102.

8.103.

8.104.

8.105.

8.106.

8.107.

8.108.

8.109.

8.110.

8.8. Списки PROLOG. Рекурсивная обработка списков

8.8.1. Определение и структура списка

Мы приводили рекурсивное определение списка в 8.2. Повторим его:

а) пустой список [ ] - это список;

б) [A¦B] - список, если В - список, то есть список - это упорядоченная последовательность элементов. Это определение требует ясного понимания структуры списка.

Рассмотрим несколько вариантов записи списка:

а) [1 ¦ [2, 3, 4]] здесь 1 - голова списка, а [2, 3, 4] - хвост списка, который сам обязательно является списком и может быть в свою очередь разбит на голову и хвост. Получается следующего вида дерево (рис. 8.2).

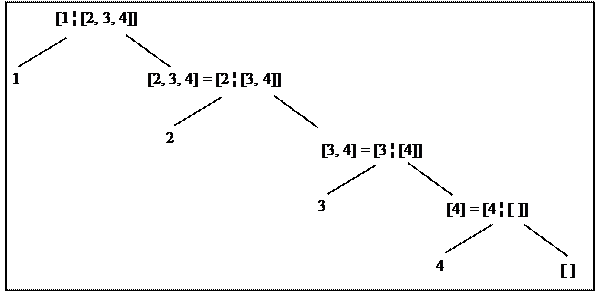Рис. 8.2. Пример представления списка [1 ¦ [2, 3, 4]]

б) [1, 2, 3, 4]. Здесь нет явно выраженной головы и хвоста списка. По умолчанию PROLOG-система положит голову равной 1, но программой может в качестве головы использовать список [1, 2]. Тогда исходный список может быть записан в виде [[1, 2]; [3, 4]]. Возможны следующие представления этого списка (рис. 8.3).

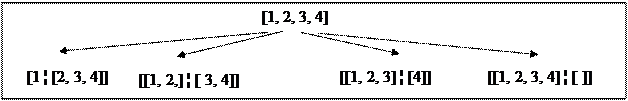
Рис. 8.3. Представления списка [1, 2, 3, 4]

Не подлежит расщеплению только пустой список. У него нет ни головы, ни хвоста. Списки широко используются для представления деревьев синтаксического разбора, грамматик, карт, графов и т.д. Заметим, что есть языки, например LISP, где списки являются единственным способом представления данных. На PROLOG список - это частный вид структуры.

8.8.2. Рекурсивная обработка списков

Основной принцип работы со списками можно сформулировать так: "если не можешь решить задачу для всего списка, попробуй решить ее для хвоста". Процедурно это означает, что на каждом шаге задача будет решаться для списка, длина которого на 1 меньше, чем у предыдущего. Естественно, для завершения прямого хода рекурсии нужно задать граничное условие. Поэтому рекурсивная программа обработки списка обязательно содержит следующие два раздела:

а) факт, являющийся граничным условием, завершающим прямой ход;

б) рекурсивное правило, которое сводит операцию над списком к операциям над хвостом.

Приведем несколько операций со списками.

Примеры

8.13.Определить число элементов в списке.

сколько ([ ], 0).

сколько ([A | B], N) if сколько (B,M), N,M+1.

? – сколько ([саша, игорь, лена], Х).

Ответ: Х=3.

8.14.Определение принадлежности элементов списку

принадлежит (X,[X ¦ _]).

принадлежит (X, [A¦Y]) if принадлежит (X,Y).

? – принадлежит (4, [1,3,4,9]).

Ответ: да.

Программа имеет очень простой декларативный смысл: элемент принадлежит списку, если он является его головой или принадлежит хвосту списка.

8.15.Соединение двух списков.

Эту задачу можно описать с помощью следующих предикатов:

а) ограничение рекурсии состоит в том, что если к пустому списку [ ] добавить список P, то в результате получиться P;

б) рекурсия состоит в том, что можно список P добавить к концу списка [X¦Y], если P будет добавлен к хвосту Y и затем присоединен к голове X (при этом получается список [X¦T]).

присоединить ([ ], P, P).

присоединить ([X¦Y], P, [X¦T] ) if присоединить (Y, P, T).

Например, если задан вопрос к этой базе знаний:

? – присоединить (L, [джим ¦ R], [джек, бил, джим, тим, джим, боб]).

То будут получены ответы:

L = [джек, бил].

R = [тим, джим, боб].

L = [джек, бил, джим, тим].

R = [боб].

Существует также традиция использовать для обозначения предиката слияния двух списков предикативный символ "append" (англ. "добавить").

В некоторых случаях постановки вопросов к такого рода программам приходиться использовать отсечение (!), например, ответ к программе:

Append ([ ], L, L).

Append ([A¦B], C, [A¦D])if append (B, C, D).

? – append (X, Y, [1, 2]).

Получается таким:

X = [ ]

Y = [1,2]

X = [1]

Y = [2]

X = [1, 2]

Y = [ ].

Если же заменить первое предложение на append ([ ], l, l) if !. и задать тот же вопрос, то получиться правильный ответ:

X = [ ]

Y = [1, 2].

8.16. Удаление элемента списка.

Программа аналогична проверке принадлежности элементов списку, но требует уже трехарного предиката, один аргумент которого указывает удаляемый элемент, второй аргумент – исходный список и третий – список-результат:

удал (X, [X¦Y], Y) : – !.

удал (X, [Z¦Y], [Z│W]) : – удал (X, Y, W).

Декларативный смысл: если удаляемый элемент совпадает с головой списка, то результатом программы является хвост списка, иначе удаления производятся из хвоста списка.

Программа удаляет первое вхождение в список элемента, связанного с переменной X. Знак отсечения "!" в конце правила предотвращает последующий поиск и вывод лишних вариантов ответов после выполнения ограничительного факта.

Для удаления всех вхождений элемента X программу надо дополнить:

удал (X, [ ], [ ]) if !.

удал (X, [X¦Y], W) : – удал (X, Y, W).

удал (X, [Z¦Y], [Z¦W]) : – удал (X, Y, W).

Декларативный смысл программы таков: пока список не пуст, удалить элемент, если он совпадает с головой списка, а затем удалить его из оставшегося хвоста, иначе надо сразу удалить элемент из хвоста.

8.17. Индексация элементов списка.

Смысл программы состоит в том, чтобы получить элемент под номером N или узнать номер элемента X:

получить ([X¦_], 1, X).

получить ([W¦Y], N, X)if N is M+1, получить (Y, M, X).

По смыслу программа аналогична подсчету элементов списка.

8.18.Поиск максимального элемента.

max ([X], X).

max ([X¦Y], X) : – max (Y, W), X >W, !.

max ([X¦Y], W) : – max (Y, W).

Декларативный смысл программы: если в списке один элемент, он и является максимальным, если более одного, то это голова списка, если она больше максимального элемента хвоста, или максимальный элемент хвоста.

8.19. Обращение списка.

Эта задача самая сложная из рассмотренных. Для ее решения важно сообразить, что обратить список из одного элемента – значит оставить список без изменения. Обратить более длинный список значит обратить его хвост, а потом в конец добавить к нему голову исходного списка:

обр ([X], [X]).

обр ([X¦Y], Z) : – обр (Y, W), присоединить (W, [X], Z).

В этой программе используется процедура слияния списков, описанная выше.

8.20. Задать два списка слов, соединить их и удалить все вхождения головы второго списка.

Domains

X, Y, Z = symbol*.

A,B=symbol.

Predicates

Dan1 (X).

Dan2 (X).

Soed (X,X,X).

Udal (A,X,X).

Clauses

Dan1 ([1,2,3,4]).

Dan2 ([4,3,4,2]).

Soed ( [ ], X, X ) if !.

Soed ( [X¦Y] ,Z, [ X¦T ] ) if soed ( Y, Z, T).

Udal (A, [ ], [ ] ) if ! .

Udal ( A, [A¦Y], Z) if udal ( A, Y, Z)

Udal (A, [ B¦Y], [B¦Z] ) if udal (A, Y, Z) .

Rezult (X, Y, Z) if dan1 (X), dan2 ( [A¦Y]), soed (X, [A¦Y], T), udal ( A, T, Z).

Процедура доказательства предиката Rezult содержит следующие действия:

1. Унификация предикатов dan1 и dan2 с фактами базы данных, при этом переменная X конкретизируется значением [1, 2, 3, 4], переменная А – значением 4, переменная Y – значением [3, 4, 2].

1. Выполняется соединение списков [1,2,3,4] и [4,3,4,2], при этом переменная T получает значение [1, 2, 3, 4, 4, 3, 4, 2].

2. Удаляется число 4, которое является головой второго списка, из списка T. При этом получается список Z=[1,2,3,3,2].

Упражнения

8.111. Объединить два списка, найти max и удалить его.

8.112. Обратить список, удалить последний элемент.

8.113. Удалить из списка заданный элемент, найти длину оставшегося списка.

8.114. Два списка обратить, объединить, найти min.

8.115. Добавить к списку заданный элемент, найти длину хвоста списка.

8.116. Один из двух списков обратить, объединить со вторым, найти max.

8.117. Обратить список, найти последний и предпоследний элементы результата.

8.118. Объединить два списка. В хвосте найти min, max.

8.119. Исключить из списка число 5, найти длину оставшегося списка.

8.120. Объединить два списка, вставить перед первым элементом число 6, найти min.

8.121. Определить, принадлежат ли числа 2, 3 списку. Если принадлежат, то совпадают ли с max?

8.122. Из первого списка исключить первый, из второго – последний элементы. Списки объединить, найти длину результата.

8.123. Входит ли в список товаров «стол»? Если да, то исключить его.

8.124. Добавить к списку товаров «обувь». Объединить список товаров со списком цен. Выяснить, есть ли товар «шляпы».

8.125. Найти последний элемент списка, удалить его и найти длину результата.

8.126. Объединить два списка, найти последний элемент, проверить, является ли он минимальным в списке.

8.127. Обратить список, найти max и удалить его.

8.128. К первому списку добавить элемент в начало, ко второму – в конец и объединить списки.

8.129. Объединить два списка, найти min и удалить его.

8.130. Найти max хвоста, длину хвоста и обратить хвост. Присоединить его к голове исходного списка.

8.131. К первому списку добавить инвертированный второй список. Найти длину результата

8.132. Найти max и min элементы. Min исключить, а max заменить нулем.

8.133. Обратить список, добавить один элемент в начало, другой – в конец списка.

8.134. Найти max результата.

8.135. Объединить два списка, найти последний и предпоследний элементы. Удалить все вхождения последнего. Найти длину результата.

8.136. Даны два списка. Из второго удалить все вхождения головы первого списка.

8.137. В списке товаров найти номер «дивана». Если он первый, то удалить, иначе заменить на «кресло».

8.138. Даны два списка. Обратить их хвосты, и объединить их.

8.139. В списке слов определить слово, следующее за «прием» и удалить все вхождения этого слова.

8.140. Инвертировать первый список. Во втором удалить последний элемент. Результаты соединить.

8.141. В списке найти min. Если это голова, то удалить все вхождения. Если нет, то заменить min на 999.

8.9. Решение логических задач на PROLOG

8.9.1. Понятие о методе резолюций

Мы познакомились с правилами логического вывода при работе PROLOG. Попробуем разобраться, какая именно логическая формализация используется при этом PROLOG-системой. Решая предложенные нами задачи, мы убедились, что однозначный ответ PROLOG дает лишь в одном случае – вывод неверен, ответ – "ложь". Если же результат – "истина", то выполняется дальнейший поиск альтернативных решений. Таким образом, процесс решения использует известный закон логики "modus ponens".

Примеры

8.21. Если верно А и верно не А

Резольвента: «ложь».

8.22. Верно А и В, верно А и В -> С, верно не С

Резольвента: не (А и В) = (не А) или (не В).

8.23. Задача о ханойской башне.

Это игра, в которой используются три стержня и набор из N дисков разного диаметра с отверстием в центре. Первоначально все диски нанизаны на левый стержень в порядке убывания диаметра к вершине стержня. Цель игры – переместить все диски на центральный стержень, используя правый как запасной. При этом перемещать можно только самый верхний диск, и нельзя ставить его на диск меньшего диаметра.

Введем предикат "переместить" с аргументами:

1) сколько дисков надо переместить;

2) с какого стержня;

3) на какой стержень;

4) какой стержень будет запасным.

Например, переместить(К,В,А,С) означает, что надо переместить К дисков со стержня В на стержень А, используя стержень С.

Строим граничное условие: на левом стержне дисков нет, то есть переместить(0,-,-,-) if!

Построим рекурсивное правило:

переместить(N,A,B,C) if M=N-1, переместить(М,А,С,В), сообщить(А,В), переместить(М,С,В,А).

сообщить(X,Y) if write ([переместили, диск, с, X, на, Y]),nl.

Декларативный смысл правила: переместить N дисков с А на В, используя С – это переместить N-1 диск с А на С, используя В, нижний диск с А переместить на В и переместить N-1 диск с С на В, используя А.

8.24. Решение задач на соответствие.

Беседуют трое друзей: Белов, Рыжов, Чернов. Брюнет сказал Белову: "Посмотри, один из нас блондин, другой – рыжий, третий – брюнет, но ни у кого цвет волос не соответствует фамилии". Какой цвет волос у каждого собеседника?

Фамилия("Белов").

Фамилия("Чернов").

Фамилия("Рыжов").

Цвет("светлый").

Цвет("рыжий").

Цвет("четный").

Соответствие(X,Y) if фамилия(X), цвет(Y), X= "Белов", not (Y= "черный"), not(Y= "светлый").

/*если Х – это Белов, а У – цвет его волос, то У – не черный и не светлый*/

Соответствие(X,Y) if фамилия(X), цвет(Y), X= "Чернов", not (Y= "черный"), not(соответствие("Белов",У)).

/*если Х – это Чернов, то он не черный и не такой как Белов*/

Соответствие(X,Y) if фамилия(X), цвет(Y), X= "Рыжов", not (соответствие("Белов",У)), not(соответствие("Чернов",У)).

/*если Х – это Рыжов, то он не такой, как Белов, и не такой, как Чернов*/

Заметим, что в приведенной задаче устанавливается взаимно-однозначное соответствие между двумя множествами. Если этих ограничений нет, то задача сильно усложняется.

Упражнения

8.142. На соревнованиях по бегу Джон, Пол и Эндрю заняли три первых места. Какое место занял каждый из них, если Пол занял не 2 и не 3 место, а Эндрю не 3.

8.143. Антон и Максим носят фамилии Шилов и Гвоздев. Какую фамилию носит каждый из них, если Максим с Шиловым живут в разных домах.

8.144. Три подружки вышли в белом, зеленом и синем платьях. Только у Ани цвета платья и туфель совпадают, ни туфли, ни платье Вали не были белыми. Наташа была в зеленых туфлях. Определить цвета платьев и туфель каждой из подруг.

8.145. На заводе работают 3 друга: слесарь, токарь и сварщик. Их фамилии Борисов, Иванов и Семенов. У слесаря нет ни братьев, ни сестер. Он – младший из друзей. Семенов, женат на сестре Борисова, старше токаря. Назвать фамилии слесаря, токаря и сварщика.

8.146. В бутылке, стакане, кувшине и банке находится молоко, квас, лимонад и вода. Известно, что молоко и вода – не в бутылке, сосуд с лимонадом находится между кувшином и сосудом с квасом, в банке – не лимонад и не вода. Стакан находится около банки и сосуда с молоком. Как распределены жидкости по сосудам?

8.147. У Ивана машина красная, у Петра – не черная, не синяя, не голубая, у Максима – черная и синяя, у Александра есть машины любого цвета (из перечисленных), у Бориса машины белого и синего цветов. У кого какого цвета машины, если все водители ехали на машинах разных цветов.

8.148. Три друга разной национальности на соревнованиях заняли 1, 2, 3 места. Зовут друзей по-разному и занимаются они разными видами спорта. Майкл предпочитает баскетбол и играет лучше американца. Англичанин Саймон играет лучше теннисиста. Игрок в крикет занял 1-ое место. Кто является австралийцем? Какое место занял Сигурд?

8.149. В гостинице за круглым обеденным столом встретились 5 гостей родом из Москвы, Петербурга, Новгорода, Перми и Томска. Их фамилии Юрин, Томин, Алешин, Николаев и Викторов. Москвич сидел между томичем и Викторовым, петербуржец – между Юриным и Томиным, а напротив него сидел пермяк и Алешин. Николаев никогда не был в Петербурге, Юрин бывал в Москве и Томске, а томич с Томиным регулярно переписываются. Определите, в каком городе живет каждый из постояльцев гостиницы.

8.150. Воронов, Панков, Левин и Сахаров – 4 талантливых человека, один из них танцор, другой художник, третий певец, четвертый писатель. Известно, что Воронов и Левин сидели в зале консерватории, когда певец давал сольный концерт; Панков и писатель вместе позировали художнику; писатель написал повесть о Сахарове и собирается писать о Воронове; Воронов никогда не слышал о Левине. Кто чем занимается?

8.151. Три рыцаря со своими оруженосцами, спасаясь от врагов, должны переправиться через реку в маленькой двухместной лодке. Но ни один оруженосец не соглашается остаться на вражеском берегу без своего хозяина. Каким образом всем шестерым удалось все же переправиться на другой берег?

8.152. Четыре друга A, B, C, D играют каждый на одном из инструментов: флейте, рояле, гитаре и скрипке. Каждый из друзей владеет одним из иностранных языков: английским, французским, немецким и испанским. Известно, что

а) юноша, играющий на гитаре, говорит по-испански;

б) B не играет ни на скрипке, ни на флейте, ни на рояле:

в) A не играет ни на скрипке, ни на флейте и не знает английского;

г) D говорит по-французски, но не играет на скрипке.

Кто на каком инструменте играет и на каком языке говорит?

8.153. По древнему поверью, у каждого месяца есть свой камень-талисман. Так, июню, июлю и сентябрю соответствуют камни рубин, сапфир и жемчуг. Эти камни означают мудрость, здоровье и благополучие. У какого месяца какой камень-талисман и что он означает, если известно, что:

а) жемчуг и рубин не соответствую сентябрю;

б) в июне и июле мудрости не наблюдается;

в) здоровье не соответствует рубину;

г) благополучие не относится к июню.

8.10. Задачи, использующие структуру графа

Графом называется совокупность вершин и ребер, соединяющих эти вершины (рис. 8.4).

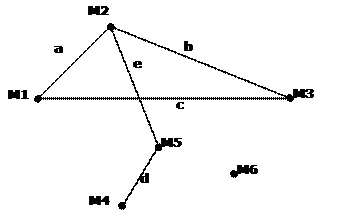
Рис. 8.4. Граф

На этом рисунке изображен граф, состоящий из 6 вершин М1,…,М6 и 5 ребер
a, b, c, d, e. Одна из вершин М6 – изолированная. Граф может быть ориентированным (если на ребрах указано направление) или неориентированным (в противном случае).

Примеры

8.25. Поиск в лабиринте.

В доме 6 комнат b, c, d, e, f, g, сведения о том, где находятся двери, представлены в виде фактов: дверь(b,e), дверь(b,c), дверь(d,e), дверь(c,d), дверь(e,f), дверь(g,e). В комнате g есть телефон. Эти связи могут быть изображены в виде графа (рис. 8.5):

Рис. 8.5. К условию примера 8.25

Задача состоит в том, чтобы путник нашел в лабиринте ту комнату, в которой находится телефон, поскольку ему срочно надо позвонить, причем нельзя дважды заходить в одну комнату.

У этой задачи могут быть варианты: путник, блуждая по лабиринту, ищет выход из него.

Введем координаты перехода (X,Y,T), который истинен, если можно перейти из комнаты Х в комнату Y, имея список Т пройденных комнат. Тогда грамотное условие рекурсивности поиска может быть записано так:

переход (Х,Х,Т) if !.

/* всегда можно перейти из Х в Х, оставаясь в ней*/

Рекурсивное правило сформулируем так: выбираем смежную с Х комнату Z и дописываем Z в список Т. Получится:

переход (X,Y,T) if дверь (X,Z), not (принадлежит (Z,T)), переход (Z,Y , [Z¦T] ).

Но кроме варианта дверь(X,Z) нас устроит вариант дверь(Z,X). Поэтому к имеющемуся рекурсивному правилу следует добавить:

переход (X,Y,T) if дверь(Z,X), not (принадлежит(Z,T)), переход (Z, Y, [Z¦T]).

Для завершения задачи следует ввести факт, ограничивающий процесс поиска, например: телефон есть в комнате g; или сокровище находится в комнате е и т.д. Если факт есть телефон(g) введен в БД, то вопрос можно задать так:

Переход (a,X,[ ]), есть_телефон(Х).

Постарайтесь сформулировать вопросы самостоятельно.

Упражнения

8.154. Нарисовать конверт (рис. 8.6), не отрывая карандаша от бумаги и не проводя 2 раза по одной и той же линии. Результат – список пройденных ребер графа.

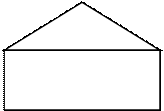
Рис. 8.6. К условию упражнения 8.154

8.155. Имеется база данных о дорогах между 5-ю городами. Определить, как можно проехать из одного заданного пункта в другой.

8.156. Дана база данных дороги (X,Y,расстояние). Определить самый короткий путь из заданного пункта в другой.

8.157. Определить, в какие города можно уехать из пункта Р, если в БД задана сеть дорог. Определить, в какие города нельзя доехать из пункта Р.

8.158. Определить, есть ли в БД "дороги" (X,Y) пункт, который соединен со всеми остальными.

8.159. Определить, является ли система дорог зве здой (рис. 8.7).

Рис. 8.7. К условию упражнения 8.159

8.160. Пять городов соединены телефоном только попарно. В каждом городе живет книголюб, имеющий ранние издания двух редких книг. Определить, может ли книголюб из заданного пункта обменяться книгами с книголюбом из другого города? Если да, то через какие города?

Рис. 8.8. К условию упражнения 8.160

8.161. Телефонная сеть между 6 городами оплачена так:

сеть(X,Y,стоимость 1-ой минуты).

Определить, можно ли позвонить из пункта 12 в пункт 14 и сколько будет стоить 1 минута разговора, если стоимости складываются при сложении путей.

8.162. Имеется 4 города, расстояния между которыми известны. Требуется проложить дорогу так, чтобы она проходила через каждый город. Вывести все возможные варианты работ и полученный километраж.

8.163. Для предыдущей задачи вывести все варианты работ, при которых километраж ≤500.

8.164. Бригада артистов должна выступить в городах N1, N2, N3, соединенных дорогами. Составить маршрут бригады, при котором длина пути была бы минимальной.

Из города N1 есть дороги в города N2, N3, N4, из которых соединены дорогой N2 и N3. Определить, можно ли послать посылку почтой из одного заданного города в другой. Если да, то по какому маршруту.