В) алгоритм цифровой подписи rsa
ОСНОВНЫЕ РЕЖИМЫ РАБОТЫ АЛГОРИТМА RSA
A) Алгоритм создания открытого и секретного ключей в RSA
Алгоритм Ривеста-Шамира-Эдлемана(RSA). Этот алгоритм носит инициалы его изобретателей. Он имеет важное значение, поскольку может быть использован как для шифрования, так и для цифровых подписей. Стойкость алгоритма RSA определяется сложностью разложения больших чисел на множители. (Наверное, криптоанализ шифра RSA возможен и без использования операции разложения на множители, но никто до сих пор не доказал этого).
RSA-ключи генерируются следующим образом:
1. Выбираются два различных случайных простых числа p и q заданного размера (например, 1024 бита каждое).
2. Вычисляется их произведение n = pq, которое называется модулем.
3. Вычисляется значение функции Эйлера от числа n: φ(n) = (p − 1)(q − 1).
4. Выбирается целое число e (1 < e < φ(n)), взаимно простое со значением функции φ(n). Обычно в качестве e берут простые числа, содержащие небольшое количество единичных битов в двоичной записи, например, простые числа Ферма 17, 257 или 65537.
Примечание Целые числа называются взаимно простыми, если они не имеют никаких общих делителей, кроме ±1. Примеры: 14 и 25 взаимно просты, а 15 и 25 не взаимно просты (у них имеется общий делитель 5).
Число e называется открытой экспонентой (англ. public exponent)
Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в e.
Слишком малые значения e, например 3, потенциально могут ослабить безопасность схемы RSA.
5. Вычисляется число d, мультипликативно обратное к числу e по модулю φ(n), то есть число, удовлетворяющее условию:
или: d∙e = 1 + kφ(n), где k — некоторое целое число. d∙e – kφ(n) = 1
Примечание: Можно вычислять и так (e∙d) mod ((p-1)∙(q-1)) = 1.
В приведенных выше уравнениях "mod" означает остаток. Например, 12 mod 10 = 2. Два - это остаток от деления 12 на 10.
Значит d будет, например 7. (Может быть и другим, например 27).
Число d называется секретной экспонентой.
Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
6. Пара e, n публикуется в качестве открытого ключа RSA (англ. RSA public key).
7. Пара d, n играет роль секретного ключа RSA (англ. RSA private key) и держится в секрете.
Б) Шифрование и расшифрование
Предположим, Боб хочет послать Алисе сообщение 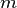 .
.
Сообщениями являются целые числа в интервале от 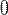 до
до 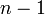 , т.е
, т.е 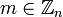 .
.

Алгоритм:[14] · Взять открытый ключ 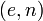 Алисы · Взять открытый текст Алисы · Взять открытый текст 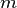 · Зашифровать сообщение с использованием открытого ключа Алисы: · Зашифровать сообщение с использованием открытого ключа Алисы: 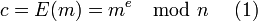 Алгоритм: · Принять зашифрованное сообщение Алгоритм: · Принять зашифрованное сообщение 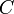 · Взять свой закрытый ключ · Взять свой закрытый ключ 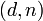 · Применить закрытый ключ для расшифрования сообщения: · Применить закрытый ключ для расшифрования сообщения: 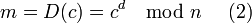 |
Корректность схемы RSA
Уравнения 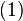 и
и 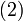 , на которых основана схема RSA, определяют взаимно обратные преобразования множества
, на которых основана схема RSA, определяют взаимно обратные преобразования множества 
В) Алгоритм цифровой подписи RSA
Система RSA может использоваться не только для шифрования, но и для цифровой подписи.
Предположим, что стороне 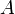 нужно отправить стороне
нужно отправить стороне 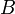 ответ
ответ 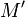 , подтверждённый цифровой подписью.
, подтверждённый цифровой подписью.

Базовый алгоритм, позволяющий обеспечить конфиденциальность данных, очень прост.
Шифрованный текст = (открытый текст)e mod n
Открытый текст = (шифрованный текст)d mod n
Секретный ключ = {d, n}
Открытый ключ = {e, n}
Алгоритм: · Взять открытый текст 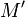 · Создать цифровую подпись · Создать цифровую подпись 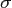 с помощью своего секретного ключа с помощью своего секретного ключа 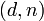 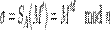 · Передать пару · Передать пару 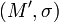 , состоящую из сообщения и подписи. , состоящую из сообщения и подписи. | Алгоритм: · Принять пару 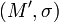 · Взять открытый ключ · Взять открытый ключ 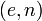 стороны стороны 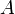 · Проверить подлинность подписи: · Проверить подлинность подписи: 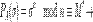 подпись верная подпись верная |
Поскольку цифровая подпись обеспечивает как аутентификацию автора сообщения, так и подтверждение целостности содержимого подписанного сообщения, она служит аналогом подписи, сделанной от руки в конце рукописного документа.
Важное свойство цифровой подписи заключается в том, что её может проверить каждый, кто имеет доступ к открытому ключу ее автора. Один из участников обмена сообщениями после проверки подлинности цифровой подписи может передать подписанное сообщение ещё кому-то, кто тоже в состоянии проверить эту подпись. Например, сторона 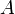 может переслать стороне
может переслать стороне 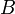 электронный чек. После того как сторона
электронный чек. После того как сторона 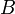 проверит подпись стороны
проверит подпись стороны 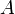 на чеке, она может передать его в свой банк, служащие которого также имеют возможность проверить подпись и осуществить соответствующую денежную операцию.
на чеке, она может передать его в свой банк, служащие которого также имеют возможность проверить подпись и осуществить соответствующую денежную операцию.
Заметим, что подписанное сообщение 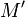 не зашифровано. Оно пересылается в исходном виде и его содержимое не защищено. Путём совместного применения представленных выше схем шифрования и цифровой подписи в системе RSA можно создавать сообщения, которые будут и зашифрованы, и содержать цифровую подпись. Для этого автор сначала должен добавить к сообщению свою цифровую подпись, а затем — зашифровать получившуюся в результате пару (состоящую из самого сообщения и подписи к нему) с помощью открытого ключа принадлежащего получателю. Получатель расшифровывает полученное сообщение с помощью своего секретного ключа. Если проводить аналогию с пересылкой обычных бумажных документов, то этот процесс похож на то, как если бы автор документа поставил под ним свою печать, а затем положил его в бумажный конверт и запечатал, с тем чтобы конверт был распечатан только тем человеком, кому адресовано сообщение. Основным недостатком шифра RSA и других алгоритмов с открытым ключом, является их низкая производительность, по сравнению с алгоритмами с секретным ключом. Алгоритм RSA уступает по скорости сопоставимым реализациям алгоритма DES в 100, а то и в 1000 раз.Хотя шифр RSA еще никому не удалось раскрыть, прогресс в математике может сделать этот шифр устаревшим. При наличии эффективного способа разложения больших чисел на множители шифр RSA можно легко раскрыть. К тому же алгоритм RSA и другие алгоритмы с открытым ключом не защищены от множества атак, которые определяются способами использования этих алгоритмов
не зашифровано. Оно пересылается в исходном виде и его содержимое не защищено. Путём совместного применения представленных выше схем шифрования и цифровой подписи в системе RSA можно создавать сообщения, которые будут и зашифрованы, и содержать цифровую подпись. Для этого автор сначала должен добавить к сообщению свою цифровую подпись, а затем — зашифровать получившуюся в результате пару (состоящую из самого сообщения и подписи к нему) с помощью открытого ключа принадлежащего получателю. Получатель расшифровывает полученное сообщение с помощью своего секретного ключа. Если проводить аналогию с пересылкой обычных бумажных документов, то этот процесс похож на то, как если бы автор документа поставил под ним свою печать, а затем положил его в бумажный конверт и запечатал, с тем чтобы конверт был распечатан только тем человеком, кому адресовано сообщение. Основным недостатком шифра RSA и других алгоритмов с открытым ключом, является их низкая производительность, по сравнению с алгоритмами с секретным ключом. Алгоритм RSA уступает по скорости сопоставимым реализациям алгоритма DES в 100, а то и в 1000 раз.Хотя шифр RSA еще никому не удалось раскрыть, прогресс в математике может сделать этот шифр устаревшим. При наличии эффективного способа разложения больших чисел на множители шифр RSA можно легко раскрыть. К тому же алгоритм RSA и другие алгоритмы с открытым ключом не защищены от множества атак, которые определяются способами использования этих алгоритмов
Классификация VPN
Классифицировать VPN решения можно по нескольким основным параметрам:
По степени защищенности используемой среды:
1.Защищённые-Наиболее распространённый вариант виртуальных частных сетей. С его помощью возможно создать надежную и защищенную сеть на основе ненадёжной сети, как правило, Интернета. Примером защищённых VPN являются: IPSec, OpenVPN и PPTP.
2.Доверительные- Используются в случаях, когда передающую среду можно считать надёжной и необходимо решить лишь задачу создания виртуальной подсети в рамках большей сети. Проблемы безопасности становятся неактуальными. Примерами подобных VPN решений являются: Multi-protocol label switching (MPLS) и L2TP (Layer 2 Tunnelling Protocol) (точнее сказать, что эти протоколы перекладывают задачу обеспечения безопасности на другие, например L2TP, как правило, используется в паре с IPSec).
По способу реализации
