Основна теорема інформаційного приховування при активній протидії порушнику
Исследуем скрытую ПС (пропускную способность) при активном противодействии нарушителя, стремящегося разрушить скрытно передаваемую информацию. Информаци-онно-скрывающее противоборство между отправителем сообщений и ата-кующим удобно описать методами теории игр. Цена игры равна величине скрытой ПС. Для максимизации скрытой ПС (максимизации платежа) скры-вающий информацию оптимально строит скрывающее преобразование. Для минимизации скрытой ПС (минимизации платежа) атакующий синтезирует оптимальное атакующее воздействие. Величина скрытой ПС может быть по-лучена последовательным соединением скрывающего преобразования и ата-кующего воздействия. Оценим величину скрытой ПС для стегосистемы с двоичным алфавитом. Исследуем теоретико-игровые аспекты проблемы скрытия информации стегосистемами.
Рассмотрим теорему, которая названа в [2] основной теоремой информа-ционного скрытия при активном противодействии нарушителя. Для любых произвольно сложных стегосистем и любых атак без памяти эта теорема ограничивает сверху скорость безошибочной передачи для скрывающего информацию при условии, что атакующий знает описание скрывающего преобразования, а декодер знает описание и скрывающего преобразования и атакующего воздействия. Данное условие на самом деле не является трудновыполнимым, как это кажется на первый взгляд. Даже если стратегии действий скрывающего информацию и атакующего неизвестны, но стационарны, то можно утверждать, что и атакующий и декодер потенциально способны определить их, обработав достаточно большой объем статистического материала. Это допущение вполне реалистично, хотя и не всегда может быть достигнуто на практике из-за высокой вычислительной сложности.
Представляется вполне логичным, что величина скрытой ПС равна взаимной информации между стего 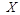 и искаженным стего
и искаженным стего 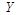 при условии, что отправителю и получателю скрываемой информации известен пустой контейнер
при условии, что отправителю и получателю скрываемой информации известен пустой контейнер 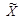 .
.
Для практических систем защиты информации, если секретным ключом стегосистемы является описание используемого контейнера, возникают две проблемы. Во-первых, получатель должен знать исходный контейнер, что ограничивает возможную область применения таких стегосистем. Во-вторых, отправитель и получатель скрываемых сообщений должны использовать секретную ключевую информацию очень большого объема, что неудобно на практике.
ІV клас стегосистем.
Другое возможное описание процесса внедрения получим, представив стегосистему как систему связи с передачей дополнительной информации. В этой модели кодер и декодер имеют доступ, помимо ключа, к информации о канале (то есть о контейнере и о возможных атаках). В зависимости от положения переключателей А и Б выделяют четыре класса стегосистем (подразумевается, что ключ всегда известен кодеру и декодеру).
IV класс: дополнительная информация известна и в кодере и в декодере (оба ключа замкнуты). По всей видимости все перспективные стегосистемы должны строиться по этому принципу. Оптимальность этой схемы достигается путем оптимального согласования кодера с сигналом-контейнером, а также адаптивным управлением декодером в условиях наблюдения канала атак.
