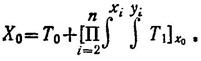Синхронные рассуждения

Очевидно, что с практической точки зрения наиболее интересны и трудны для анализа случаи взаимной рефлексии игроков. Из сказанного ясно, что преимущество находится на стороне игрока, обладающего более высоким рангом реф-

­ Конец страницы 30 ­

¯ Начало страницы 31 ¯

лексии. Однако в жизни большей частью в конфликт вступают игроки, обладающие примерно одинаковыми имитационными способностями. Возникающие при этом трудности иллюстрируются следующим примером.

Представим себе следующую ситуацию. Пусть X и Y —противники, вооруженные пистолетами. Если X застрелит Y, то X получит какую-то сумму (пусть это будет 10 пиастров). Если Y застрелит X, то Y получит 10 пиастров. Если оба бездействуют, то оба остаются «при своих». Игроки не несут ни моральной, ни юридической ответственности, если оказываются убийцами, и не руководствуются никакими этическими принципами. Решения принимаются игроками независимо и связаться друг с другом они не могут. Спрашивается, как они должны поступить?

Изобразим игру ввиде матрицы:

	Выстрел Y	Бездействие
Выстрел X	— ∞; — ∞	10; — ∞
Бездействие	— ∞; 10	0; 0

Не правда ли, знакомая дилемма, где один из платежей только эквивалентен смерти?

Игрок X проводит такое рассуждение: «Предположим, я выстрелю, тогда я либо выиграю, либо погибну. Если я не выстрелю, я наверняка не выиграю, но вероятность моей гибели не станет меньше. Ведь У принимает решение независимо от того, что думаю я. Поэтому я должен выстрелить. Но противник проведет именно такое же рассуждение и тоже нажмет на спусковой крючок и я погибну. Да, но ведь он тоже придет к этой же мысли, то есть, что я выстрелю. Может быть, если я не выстрелю, — и он не нажмет на крючок. Нет, не проходит — ведь наши решения не связаны. Конечно, нам обоим выгодно бездействовать. Это очевидно, он это выведет и так поступит. Ага, тогда я выстрелю и выиграю 10 пиастров. Но ведь к такому же решению придет и он...».

Здесь воспроизведено рассуждение игрока, который пытается принять решение и сталкивается с непрерывными противоречиями. Оба варианта решения одинаково неубедительны. Чтобы выявить причину парадокса, представим себе следующую ситуацию: пусть эти двое, вооруженные пистолетами, разделены перегородкой из тонкой зеркальной фольги, которая не является препятствием для пули. Игрок видит свое отражение в зеркале и рассматривает его как модель

­ Конец страницы 31 ­

¯ Начало страницы 32 ¯

своего противника¹. Он медленно поднимает пистолет и видит, что модель противника также поднимает пистолет. Игрок понимает, что если он нажмет на крючок, то и модель нажмет на крючок. Поскольку эта модель—единственное средство прогнозировать поведение противника, то свой выстрел порождает выстрел модели. Игрок медленно опускает пистолет, противник делает то же самое. «Я сейчас его обману», — думает игрок и тут же видит хитроватое выражение лица модели и предупредительное движение пистолета.

Рассуждение игрока, приведенное выше, рождено именно такой ситуацией с зеркалом. Здесь игрок пользуется самим собой как моделью своего противника. Любая мысль, которая приходит ему в голову, автоматически приходит в голову его сопернику. Игроки стоят друг перед другом, синхронно реагируют и синхронно читают мысли друг друга. Игрока X в этой драматической ситуации можно изобразить символической суммой:

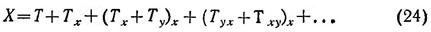
Тот факт, что игрок стоит перед зеркалом, фиксируется симметрией каждого слагаемого, заключенного в скобки, относительно индексов х и у. Каждое слагаемое в (24) мы можем интерпретировать как своеобразные «кадры» мысли, «пробегающие» в сознании игроков, как сменяющие друг друга кадры кинофильма. Очевидно, что игрок, на «экране» которого пробегают подобные кадры, может вывести, что сам факт выстрела является приговором самому себе, и примет решение, исходя из этого вывода. В этой особенности синхронных рассуждений и кроется причина парадоксов типа «дилеммы заключенного». Другими словами, логическая природа этой дилеммы может быть объяснена самим механизмом принятия решения игроками, механизмом, осуществляющимся по схеме (24).

Используя ранее введенную символику, мы можем изобразить динамический процесс во внутреннем мире игрока, находящегося в состоянии «дилеммы заключенного», следующим образом: