Общие сведения и понятия
СОДЕРЖАНИЕ
| Введение | ||
| Теоретическая часть | ||
| 1.1 | Общие сведения и понятия | |
| 1.2 | Виды сигналов | |
| 1.3 | Дискретизация непрерывных сигналов по В.А. Котельникову | |
| 1.4 | Воспроизведение сигналов | |
| 1.5 1.6 1.7 | Квантование сигналов Погрешности, возникающие при дискретизации, квантовании и воспроизведении непрерывных сигналов Частотная модуляция | |
| Расчетная часть | ||
| 2.1 | Расчет интервала дискретизации по теореме В.А.Котельникова и построение графика непрерывного сигнала | |
| 2.2 | Вычисление погрешности воспроизведения заданного сигнала в момент времени tx, возникающей за счет дискретизации Uн(t) по времени | |
| Заключение | ||
| Список литературы | ||
ВВЕДЕНИЕ
Человеческое общество живет в информационном мире, который постоянно изменяется и пополняется. То, что человек видит, слышит, помнит, знает, переживает, все это различные формы информации. Следовательно, в широком смысле информацию можно определить как совокупность знаний об окружающем нас мире. В таком понимании информация является важнейшим ресурсом научно-технического прогресса и социально-экономического развития общества и наряду с материей и энергией принадлежит к фундаментальным философским категориям естествознания. Понятия «информация» (от лат. informatio - разъяснение, изложение) и «сообщение» в настоящее время неразрывно связаны между собой. Эти близкие по смыслу понятия сложны, и дать их точное определение через более простые нелегко. Информация - это совокупность сведений или данных о каких-либо событиях, явлениях или предметах, то есть это совокупность знаний об окружающем нас мире. Передача и хранение информации осуществляется с помощью различных знаков (символов), которые позволяют представить её в некоторой форме. Сообщение это совокупность знаков, отображающих ту или иную информацию. Передача сообщений (а, следовательно, и информации) на расстояние осуществляется с помощью какого-либо материального носителя, например, бумаги или магнитной ленты или физического процесса, например, звуковых или электромагнитных волн, тока и т.д. Сигнал - это физический процесс, отображающий (несущий) передаваемое сообщение. В качестве сигналов в настоящее время в основном используются электрические и оптические сигналы. В электронике сигналом может быть все - от компьютерных цифровых импульсов и до импульсов, модулированных радиоволнами УКВ-диапазона. Сигнал передаёт (развёртывает) сообщение во времени, то есть всегда является функцией времени. Сигналы формируются путём изменения тех или иных параметров физического носителя в соответствии с передаваемым сообщением. Сообщения могут быть функциями времени, например речь при передаче телефонных разговоров, температура или давление при передаче телеметрических данных, спектакль при передаче по телевидению и т.п. В других случаях сообщение не является функцией времени (например, текст телеграммы, неподвижное изображение и т.д.).
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Общие сведения и понятия
В технических отраслях знаний термин «сигнал» (от латинского signum – знак) очень часто используется в широком смысловом диапазоне, без соблюдения строгой терминологии. Под ним понимают и техническое средство для передачи, обработки и использования информации, а по существу, материальный носитель определенного информационного сообщения; и физический процесс, представляющий собой материальное воплощение информационного сообщения - изменение какого-либо параметра носителя информации во времени, в пространстве или в зависимости от изменения значений каких-либо других аргументов; и форму представления данных в виде последовательности значений определенной скалярной величины, как правило – амплитуды, измеренной во времени; и смысловое содержание определенного физического состояния или процесса, как, например, сигналы светофора, звуковые предупреждающие сигналы и т.п.
Применительно к процессам регистрации и обработки результатов наблюдений, которые имеют место во всех областях науки и техники, понятие «сигнал» очень часто отождествляют с понятиями «данные» и «информация». Действительно, эти понятия взаимосвязаны и не существуют одно без другого, но относятся к разным категориям.
Информация (от латинского informatio - разъяснение, осведомление, изложение), наряду с материей и энергией, принадлежит к фундаментальным философским категориям естествознания. По определению Норберта Винера, основоположника кибернетики, «информация есть информация, а не материя или энергия».
Информация обладает определенными свойствами.
Первое свойство — способность управлять построением всех физических структур, начиная от электрона и заканчивая живыми организмами. Базируется это свойство на положении о том, что каждая элементарная частица (электрон) несет информацию о самой себе.
Второе свойство — способность сохраняться в течение любых промежутков времени. К примеру, молекула РНК хранит в себе некий чертеж, который может представлять собой чертеж простейшего организма (вируса) или чертеж столь сложной системы, как человеческий организм. Несмотря на сложность, она весьма стабильна и в широком диапазоне изменения внешних условий сохраняется сколь угодно долго!
Третье свойство (противоположное второму) — способность изменяться во времени. Возможно как разрушение, так и совершенствование информации.
Четвертое свойство — способность переходить из пассивной формы (информация просто хранится и никак не проявляется) в активную (информация непосредственно участвует в процессе построения некоторой структуры). Обратное этому свойству — процесс запоминания или записи информации (то есть перехода ее из активной в пассивную форму).
Пятое свойство — способность быть переданной на расстояние. Это свойство непосредственно следует из свойства информации к сохранению.
Шестое свойство — способность подвергаться переработке. Например, в живой природе молекула РНК управляет синтезом конкретного белка, выбранного из бесчисленного множества, всегда без сбоев и ошибок.
Седьмое свойство — способность подвергаться измерению. Если информация — физическая величина, то ее можно измерить
Впервые такую меру предложил в 1928 г. американский ученый Р.Хартли. Измерить количество информации, по Хартли, — значит пересчитать количество возможностей, одна из которых реализуется в данный момент, а затем взять логарифм от этого количества.
Что касается данных (от латинского datum – факт), то это совокупность фактов (результатов наблюдений, измерений) о каких-либо объектах, явлениях или процессах материального мира, представленных в определенном (количественном или качественном) и, как правило, формализованном виде. Это не информация, а только атрибут информации - сырье для получения информации путем соответствующей обработки и интерпретации.
Принимая во внимание изложенное, под термином «сигнал» в строгом смысле этого слова в данном курсе будем понимать определенным образом организованное отображение определенных данных о характере изменения в пространстве, во времени или по любой другой переменной физических величин, физических свойств или физического состояния объекта исследований. А так как данные содержат определенную информацию, как об основных целевых параметрах объекта исследований, так и о различных сопутствующих и мешающих факторах измерений, то в широком смысле этого слова можно считать, что сигнал является отображением общей измерительной информации. При этом материальная форма носителей сигналов, равно как и форма их отображения, значения не имеет.
Сигнал - это информационная функция, несущая сообщение о физических свойствах, состоянии или поведении какой-либо физической системы, объекта или среды, а цель обработки сигналов - извлечение сведений, которые отображены в этих сигналах и преобразование этой информации в форму, удобную для восприятия и использования.
С понятием сигнала неразрывно связан термин регистрации сигналов, использование которого также широко и неоднозначно, как и самого термина сигнал. В наиболее общем смысле под этим термином можно понимать операцию выделения информационного сигнала и его преобразования в форму, удобную для дальнейшего использования, обработки и восприятия. Так, при получении информации о физических свойствах каких-либо объектов под регистрацией сигнала понимают процесс измерения физических свойств объекта и перенос результатов измерения на материальный носитель сигнала или непосредственное энергетическое преобразование каких-либо материальных параметров объекта в информационные параметры материального носителя сигнала (как правило, электрического). Но так же широко термин регистрации сигналов используют и для процессов выделения уже сформированных сигналов, несущих определенную информацию, из других сигналов (радиосвязь, телеметрия и пр.), и для процессов фиксирования сигналов на носителях долговременной памяти, и для многих других процессов, связанных с обработкой сигналов.
1.2 Виды сигналов
Выделяют следующие типы сигналов: аналоговый, цифровой и дискретный
Аналоговый сигнал (analog signal) является непрерывной функцией непрерывного аргумента, т.е. определен для любого значения аргументов. Источниками аналоговых сигналов, как правило, являются физические процессы и явления, непрерывные в динамике своего развития во времени, в пространстве или по любой другой независимой переменной, при этом регистрируемый сигнал подобен (“аналогичен”) порождающему его процессу. Если интервалы значений сигнала или его независимых переменных не ограничиваются, то по умолчанию они принимаются равными от -Ґ до +Ґ. Множество возможных значений сигнала образует континуум - непрерывное пространство, в котором любая сигнальная точка может быть определена с точностью до бесконечности. Примеры сигналов, аналоговых по своей природе - изменение напряженности электрического, магнитного, электромагнитного поля во времени и в пространстве
. 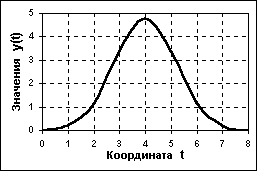
Рисунок 1.1 - Аналоговый сигнал
Дискретный сигнал по своим значениям также является непрерывной функцией, но определенной только по дискретным значениям аргумента. По множеству своих значений он является конечным (счетным) и описывается дискретной последовательностью 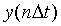 ,
, 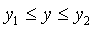 ,
, 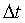 - интервал между отсчетами (интервал дискретизации сигнала), n = 0,1,2,..., N – нумерация дискретных значений отсчетов. Если дискретный сигнал получен дискретизацией аналогового сигнала, то он представляет собой последовательность отсчетов, значения которых в точности равны значениям исходного сигнала по координатам
- интервал между отсчетами (интервал дискретизации сигнала), n = 0,1,2,..., N – нумерация дискретных значений отсчетов. Если дискретный сигнал получен дискретизацией аналогового сигнала, то он представляет собой последовательность отсчетов, значения которых в точности равны значениям исходного сигнала по координатам 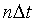 .
.
Пример дискретизации аналогового сигнала, приведенного на рисунке 1.1, представлен на рисунке 1.2. При 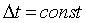 (равномерная дискретизация данных) дискретный сигнал можно описывать сокращенным обозначением y(n). При неравномерной дискретизации сигнала обозначения дискретных последовательностей (в текстовых описаниях) обычно заключаются в фигурные скобки -
(равномерная дискретизация данных) дискретный сигнал можно описывать сокращенным обозначением y(n). При неравномерной дискретизации сигнала обозначения дискретных последовательностей (в текстовых описаниях) обычно заключаются в фигурные скобки - 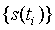 , а значения отсчетов приводятся в виде таблиц с указанием значений координат
, а значения отсчетов приводятся в виде таблиц с указанием значений координат 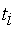 . Для коротких неравномерных числовых последовательностей применяется и следующее числовое описание:
. Для коротких неравномерных числовых последовательностей применяется и следующее числовое описание: 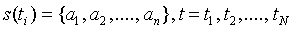 .
.
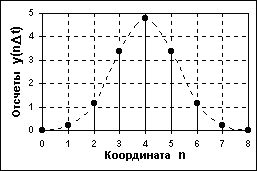
Рисунок 1.2 - Дискретный сигнал
Цифровой сигнал квантован по своим значениям и дискретен по аргументу. Он описывается квантованной решетчатой функцией 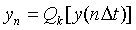 , где
, где 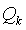 - функция квантования с числом уровней квантования k, при этом интервалы квантования могут быть как с равномерным распределением, так и с неравномерным, например - логарифмическим. Задается цифровой сигнал, как правило, в виде числового массива по последовательным значениям аргумента при
- функция квантования с числом уровней квантования k, при этом интервалы квантования могут быть как с равномерным распределением, так и с неравномерным, например - логарифмическим. Задается цифровой сигнал, как правило, в виде числового массива по последовательным значениям аргумента при 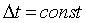 , но, в общем случае, сигнал может задаваться и в виде таблицы для произвольных значений аргумента. По существу, цифровой сигнал является формализованной разновидностью дискретного сигнала при округлении значений последнего до определенного количества цифр, как это показано на рисунке 1.2. В цифровых системах и в ЭВМ сигнал всегда представлен с точностью до определенного количества разрядов, а следовательно всегда является цифровым, С учетом этих факторов при описании цифровых сигналов функция квантования обычно опускается (подразумевается равномерной по умолчанию), а для описания сигналов используются правила описания дискретных сигналов.
, но, в общем случае, сигнал может задаваться и в виде таблицы для произвольных значений аргумента. По существу, цифровой сигнал является формализованной разновидностью дискретного сигнала при округлении значений последнего до определенного количества цифр, как это показано на рисунке 1.2. В цифровых системах и в ЭВМ сигнал всегда представлен с точностью до определенного количества разрядов, а следовательно всегда является цифровым, С учетом этих факторов при описании цифровых сигналов функция квантования обычно опускается (подразумевается равномерной по умолчанию), а для описания сигналов используются правила описания дискретных сигналов.
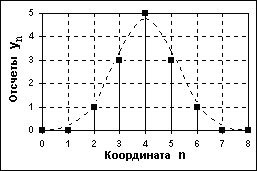
Рисунок 1.3 - Цифровой сигнал
1.4 Дискретизация непрерывных сигналов по В.А. Котельникову
Обработка информации в ЭВМ производится в числовой форме с представлением сигналов в виде последовательностей числовых значений (одно- или многомерных массивов), которые образуют дискретную функцию дискретных переменных. Числовые значения представляют собой или значения отсчетов сигнала, дискретного по своей природе, или квантованные значения выборок при дискретизации аналогового сигнала.
Для реальных задач обработки данных обычно требуется значительно меньше информации, чем ее поступает от измерительных датчиков в виде непрерывного аналогового сигнала. При этом рациональное выполнение операций дискретизации и квантования исходных данных дает возможность снизить затраты на хранение и обработку информации. Использование дискретных сигналов позволяет применять методы кодирования информации, доступные для последующего обнаружения и исправления ошибок и исключения эффекта накопления искажений.
Представление сигнала s(t) на интервале Т совокупностью дискретных значений 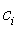 записывается в виде:
записывается в виде: 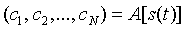 ,
,
где А - оператор дискретизации. Аналогично, для операции восстановления сигнала s(t): 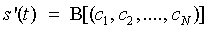 .
.
Выбор операторов А и В определяется требуемой точностью восстановления сигнала. Наиболее простыми являются линейные операторы. В общем случае:
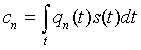 (1.1) (1.1) | |
где 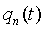 - система весовых функций. Воспроизводящая функция
- система весовых функций. Воспроизводящая функция 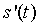 соответственно представляется аппроксимирующим полиномом:
соответственно представляется аппроксимирующим полиномом:
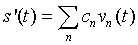 (1.2) (1.2) |
где 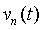 - система базисных функций. Предполагается, что базисные функции ортогональны и обеспечивают сходимость ряда к s(t) при
- система базисных функций. Предполагается, что базисные функции ортогональны и обеспечивают сходимость ряда к s(t) при 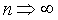 . Оптимальными являются методы дискретизации, обеспечивающие минимальный числовой ряд при заданной погрешности воспроизведения сигнала.
. Оптимальными являются методы дискретизации, обеспечивающие минимальный числовой ряд при заданной погрешности воспроизведения сигнала.
Отсчеты в выражении (1.2) связаны с операцией интегрирования, что обеспечивает высокую помехоустойчивость дискретизации. Однако в силу сложности технической реализации "взвешенного" интегрирования, последнее используется достаточно редко, при высоких уровнях помех. Более широкое распространение получили методы, при которых сигнал s(t) заменяется совокупностью его мгновенных значений 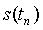 , т.е. отсчетов в моменты времени tn. Роль весовых функций в этом случае выполняют импульсы Кронекера - функции единичного отсчета
, т.е. отсчетов в моменты времени tn. Роль весовых функций в этом случае выполняют импульсы Кронекера - функции единичного отсчета 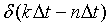 , которые равны 1 в координатной точке k = n и нулю во всех остальных точках. При этом функция
, которые равны 1 в координатной точке k = n и нулю во всех остальных точках. При этом функция 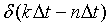 определена для любых значений
определена для любых значений 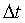 = const, но только для целых значений координат k и n.
= const, но только для целых значений координат k и n.
Отрезок времени 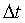 между соседними выборками называют шагом дискретизации. Дискретизация называется равномерной с частотой
между соседними выборками называют шагом дискретизации. Дискретизация называется равномерной с частотой 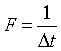 , если значение шага
, если значение шага 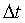 постоянно по всему диапазону преобразования сигнала. При неравномерной дискретизации значение
постоянно по всему диапазону преобразования сигнала. При неравномерной дискретизации значение 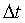 между выборками может изменяться в зависимости от изменения каких-либо параметров сигнала.
между выборками может изменяться в зависимости от изменения каких-либо параметров сигнала.
1.4 Воспроизведение сигналов
Воспроизведение сигнала по отсчетам может проводиться как на основе ортогональных, так и неортогональных базисных функций. При неортогональных базисных функциях используются, в основном, степенные алгебраические полиномы:
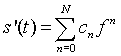 (1.3) (1.3) |
Если значения аппроксимирующего полинома совпадают со значениями выборок в моменты их отсчета, то такой полином называют интерполирующим. В качестве интерполирующих полиномов обычно используются многочлены Лагранжа.
Естественным требованием к выбору частоты дискретизации информации является внесение минимальных искажений в динамику изменения сигналов. Искажения информации будут тем меньше, чем выше частота дискретизации F, но что чем больше значение F, тем большим количеством цифровых данных будет отображаться один и тот же объем информации, а соответственно увеличивается время на ее передачу и обработку.
Следовательно, значение частоты дискретизации сигнала F должно быть необходимым и достаточным для обработки информации с заданной точностью или для восстановления аналоговых сигналов без искажений.
Интерполяционный ряд Котельникова-Шеннона является основой для операций дискретизации и восстановления аналогового сигнала, согласно которой аналоговый сигнал с ограниченным частотным спектром может быть без потерь информации преобразован в дискретный сигнал и затем точно восстановлен по его отсчетам:
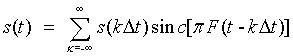 (1.4) (1.4) |
По существу, ряд представляет собой разложение сигнала по системе ортогональных функций:
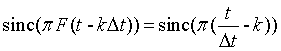 (1.5)
(1.5)
Отсюда следует, что если для частоты дискретизации сигнала справедливо неравенство 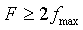 , где
, где 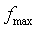 - наибольшая частота в спектре произвольной непрерывной функции s(t), то функция s(t) без потери точности может представляться в виде числовой последовательности дискретных значений
- наибольшая частота в спектре произвольной непрерывной функции s(t), то функция s(t) без потери точности может представляться в виде числовой последовательности дискретных значений 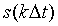 ), k = 0,1,2,..., и однозначно по этой последовательности восстанавливается. В этом и состоит сущность теоремы отсчетов Котельникова-Шеннона.
), k = 0,1,2,..., и однозначно по этой последовательности восстанавливается. В этом и состоит сущность теоремы отсчетов Котельникова-Шеннона.
1.5 Квантование сигналов
Операция квантования или аналого-цифрового преобразования (АЦП) заключается в преобразовании дискретного сигнала 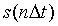 в цифровой сигнал
в цифровой сигнал 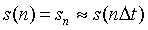 n = 0,1,2,..,N, как правило, кодированный в двоичной системе счисления.
n = 0,1,2,..,N, как правило, кодированный в двоичной системе счисления.
Сущность квантования заключается в округлении мгновенных значений входной функции s(t), до ближайших значений 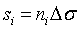 , где
, где 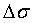 - шаг квантования шкалы цифровых отсчетов. Квантование с постоянным шагом
- шаг квантования шкалы цифровых отсчетов. Квантование с постоянным шагом 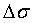 называется равномерным.
называется равномерным.
Установленный диапазон шкалы квантования от 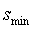 до
до 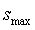 и шаг квантования
и шаг квантования 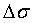 определяют число делений шкалы:
определяют число делений шкалы:
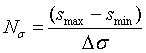 (1.6)
(1.6)
Погрешность округления 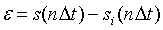 заключена в пределах
заключена в пределах 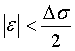 и называется шумом квантования. При достаточно малом шаге квантования любое значение в его пределах можно считать равновероятным, а значения случайной величины
и называется шумом квантования. При достаточно малом шаге квантования любое значение в его пределах можно считать равновероятным, а значения случайной величины 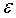 распределенными по равномерному закону:
распределенными по равномерному закону:
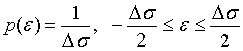 (1.7) (1.7) |
Соответственно, дисперсия и среднее квадратическое значение шума квантования:
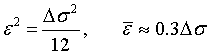 (1.8) (1.8) |
При задании уровня шума квантования с использованием последнего выражения нетрудно определить допустимое значение шага квантования.
Входной сигнал содержит, как правило, аддитивную смесь собственно сигнала s(t) и входной помехи q(t) с дисперсией соответственно 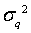 . Если помехи не коррелированны с сигналом, то после квантования суммарная дисперсия шумов:
. Если помехи не коррелированны с сигналом, то после квантования суммарная дисперсия шумов:
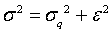 (1.9) (1.9) | |
1.6 Погрешности, возникающие при дискретизации, квантовании и воспроизведении непрерывных сигналов Если замена непрерывной функции ее отдельными значениями производится в определенные моменты времени, то этот процесс называется квантованием по времени, или дискретизацией. Горизонтальная ось времени делится на интервалы, отстоящие друг от друга на один и тот же интервал квантования 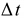 . Далее проводят вертикальные линии до пересечения с квантуемой функцией в точках 1, 2, 3, ..., 9 и определяют значения функции, начиная с . Далее проводят вертикальные линии до пересечения с квантуемой функцией в точках 1, 2, 3, ..., 9 и определяют значения функции, начиная с 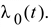 Это значит, что в интервале Т непрерывная функция Это значит, что в интервале Т непрерывная функция 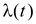 будет передаваться не бесконечным рядом значений, а в данном случае всего лишь десятью значениями. Нахождение точек, определяющих значение непрерывной функции в дискретные моменты времени, как и в квантовании по уровню, собственно процесс квантование по времени и заканчивается. В том случае, если желают восстановить квантованную функцию, осуществляют один из видов интерполяции, например, ступенчатую. При этом проводят из точек 0, 1, 2, ..., 9 горизонтальные линии до пересечения их с вертикальными линиями, т.е. линии 0-1', 1 - 2' и т.д. Далее точки 1'-1, 2'-2, 3'-3 и т.д. соединяют и получают ломаную квантованную функцию будет передаваться не бесконечным рядом значений, а в данном случае всего лишь десятью значениями. Нахождение точек, определяющих значение непрерывной функции в дискретные моменты времени, как и в квантовании по уровню, собственно процесс квантование по времени и заканчивается. В том случае, если желают восстановить квантованную функцию, осуществляют один из видов интерполяции, например, ступенчатую. При этом проводят из точек 0, 1, 2, ..., 9 горизонтальные линии до пересечения их с вертикальными линиями, т.е. линии 0-1', 1 - 2' и т.д. Далее точки 1'-1, 2'-2, 3'-3 и т.д. соединяют и получают ломаную квантованную функцию 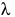 '(t). Очевидно, что чем больше дискретных значений передается за время Т, т.е. чем меньше шаг квантования '(t). Очевидно, что чем больше дискретных значений передается за время Т, т.е. чем меньше шаг квантования  t, тем с большей точностью будет восстановлена на приеме функция t, тем с большей точностью будет восстановлена на приеме функция 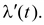 Однако излишне малая величина Однако излишне малая величина  t увеличивает массив измеренных значений и для их запоминания требуется больший объем памяти. В то же время при чрезмерно большом шаге квантования воспроизводимая функция будет не очень точной и сильно искаженной. Шаг квантования можно определить из теоремы Котельникова, смысл которого заключается в следующим: любая непрерывная функция, спектр частот которой ограничен частотой Fмакс, может быть полностью восстановлена по ее дискретным значением, взятым через интервалы времени. t увеличивает массив измеренных значений и для их запоминания требуется больший объем памяти. В то же время при чрезмерно большом шаге квантования воспроизводимая функция будет не очень точной и сильно искаженной. Шаг квантования можно определить из теоремы Котельникова, смысл которого заключается в следующим: любая непрерывная функция, спектр частот которой ограничен частотой Fмакс, может быть полностью восстановлена по ее дискретным значением, взятым через интервалы времени. 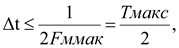 (1.10) Однако имеется ряд ограничений для практичного применения этой теоремы. Так, все сообщения, передаваемые в телемеханике, ограничения во времени. Например, если предавать синусоидальное напряжение с частотой в 50 Гц бесконечно долго во времени, то для восстановления его формы его формы на приеме достаточно передать за период лишь два импульса, соответствующих амплитудным значениям: один - положительной полуволне, другой - отрицательной. если же предавать синусоидальное напряжение в конечном отрезке времени, например, то для восстановления формы этого радиоимпульса необходимо уже не два, а значительно больше импульсов, хотя точно указать их число невозможно из - за того, что спектр частот радиоимпульсов бесконечен. (1.10) Однако имеется ряд ограничений для практичного применения этой теоремы. Так, все сообщения, передаваемые в телемеханике, ограничения во времени. Например, если предавать синусоидальное напряжение с частотой в 50 Гц бесконечно долго во времени, то для восстановления его формы его формы на приеме достаточно передать за период лишь два импульса, соответствующих амплитудным значениям: один - положительной полуволне, другой - отрицательной. если же предавать синусоидальное напряжение в конечном отрезке времени, например, то для восстановления формы этого радиоимпульса необходимо уже не два, а значительно больше импульсов, хотя точно указать их число невозможно из - за того, что спектр частот радиоимпульсов бесконечен. 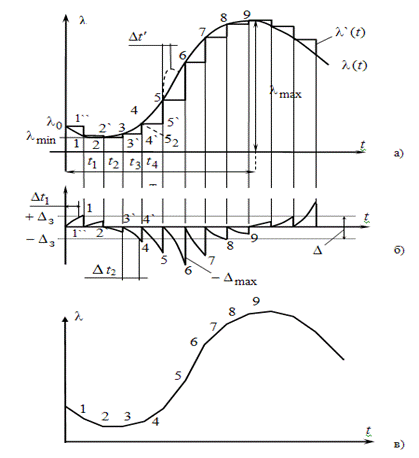 Рисунок 1.4 - Квантование сообщения по времени: а - метод квантования и восстановление функции ступенчатой интерполяцией; б - погрешности квантования; в - восстановление функции линейной интерполяцией Практически теорему Котельникова можно принять со следующей поправкой: Рисунок 1.4 - Квантование сообщения по времени: а - метод квантования и восстановление функции ступенчатой интерполяцией; б - погрешности квантования; в - восстановление функции линейной интерполяцией Практически теорему Котельникова можно принять со следующей поправкой: 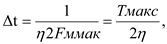 (1.11) где η - коэффициент, зависящий от точности воспроизведения функции и способа интерполяции: при линейной ηл = 0, 75/ (1.11) где η - коэффициент, зависящий от точности воспроизведения функции и способа интерполяции: при линейной ηл = 0, 75/ 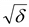 и при ступенчатой ηст = (3-5) ηл (δ - относительная погрешность в %) Существует и другой подход определения шага квантования, исходящий из задаваемой величины погрешности, близких к треугольникам, величины абсолютных погрешностей, возникающих при квантовании; эти фигуры подобны. Заданная величина абсолютной погрешности ∆3 на одном участке нарастания функции λ(t) достигается за период ∆t, на другом за ∆t2, а на некоторых она оказывается меньше заданной (например, на участке 1` - 2`). Это зависит от скорости нарастания функции λ=dλ/dt. Очевидно, следует выбрать такой шаг квантования, который соответствует максимальной скорости нарастания функции и при ступенчатой ηст = (3-5) ηл (δ - относительная погрешность в %) Существует и другой подход определения шага квантования, исходящий из задаваемой величины погрешности, близких к треугольникам, величины абсолютных погрешностей, возникающих при квантовании; эти фигуры подобны. Заданная величина абсолютной погрешности ∆3 на одном участке нарастания функции λ(t) достигается за период ∆t, на другом за ∆t2, а на некоторых она оказывается меньше заданной (например, на участке 1` - 2`). Это зависит от скорости нарастания функции λ=dλ/dt. Очевидно, следует выбрать такой шаг квантования, который соответствует максимальной скорости нарастания функции 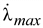 . Если бы на участке кривой 5-6 имелся всплеск функции (пунктир), то выбранный шаг квантования . Если бы на участке кривой 5-6 имелся всплеск функции (пунктир), то выбранный шаг квантования  t оказался бы излишне большим и этот всплеск не был бы восстановлен (следовало бы взять шаг t оказался бы излишне большим и этот всплеск не был бы восстановлен (следовало бы взять шаг 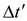 ). ). 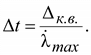 (1.12) Если считать, что максимальная скорость нарастания сохраняется во всем диапазоне изменения сообщения от нуля до максимального значения, то минимальное время изменения сообщения во всем диапазоне (1.12) Если считать, что максимальная скорость нарастания сохраняется во всем диапазоне изменения сообщения от нуля до максимального значения, то минимальное время изменения сообщения во всем диапазоне 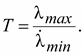 (1.13) Восстановить квантованную по времени функцию на приемной стороне можно при помощи ступенчатой или линейной интерполяции или используя метод Котельникова. Чаще всего применяется ступенчатая интерполяция, и наиболее редко используется фильтрация по Котельникову. Ступенчатая интерполяция а) выполняется с помощью запоминающих устройств, сохраняющих значения (1.13) Восстановить квантованную по времени функцию на приемной стороне можно при помощи ступенчатой или линейной интерполяции или используя метод Котельникова. Чаще всего применяется ступенчатая интерполяция, и наиболее редко используется фильтрация по Котельникову. Ступенчатая интерполяция а) выполняется с помощью запоминающих устройств, сохраняющих значения 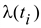 до появления следующего значения до появления следующего значения 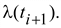 Под погрешностью интерполяции понимается разность между мгновенными значениями восстановленного и исходного символов, взятых в одни и те же моменты времени. Максимальная погрешность возникает в точках 1', 2', ..., 9'. Погрешность равна нулю в точках 1, 2, 3, ..., 9. В общем случае задаются среднеквадратичные значения этой погрешности: Под погрешностью интерполяции понимается разность между мгновенными значениями восстановленного и исходного символов, взятых в одни и те же моменты времени. Максимальная погрешность возникает в точках 1', 2', ..., 9'. Погрешность равна нулю в точках 1, 2, 3, ..., 9. В общем случае задаются среднеквадратичные значения этой погрешности: 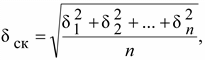 (1.14) где n - число замеров. При восстановлении квантованной функции по Котельникову нужно знать все дискретные точки, как предыдущие, так и последующие, или во всяком случае для практической реализации должно быть известно несколько точек до и после интервала, в котором происходит интерполяция. Знание последующих точек возможно, лишь в системах, допускающих запаздывание в передаче информации. Большинство телемеханических систем работает в реальном масштабе времени и не допускает запаздывания. В таких системах приходится использовать ступенчатую интерполяцию, так как для линейной, нужно знать наперед хотя бы одну точку, что опять требует запаздывания. Действительно, если, например, известно значение функции в момент t4, т. 4), то при ступенчатой интерполяции нам заранее известно, что через ∆t значение функции будет тем же (т. 5`). Каким оно будет при линейной интерполяции через интервал ∆t, неизвестно: то ли значение возрастает (т. 5), то ли уменьшится (т. 52). Иногда восстановление функции, квантованной по времени, с шагом, подсчитанным по теореме Котельникова, производится при помощи фильтра НЧ, который выделяет постоянную составляющую и низкочастотные составляющие, соответствующие спектру передаваемой функции. Однако при этом возникают погрешности из-за того, что амплитудно-частотная характеристика реального фильтра отличается от характеристики идеального фильтра. Восстановление при помощи фильтра имеет смысл, если спектр передаваемой функции достаточно сосредоточен в области нуля по оси частот. Зачастую квантование по времени используется для осуществления амплитудно - импульсной модуляции. 1.7 Частотная модуляция Частотная модуляция (ЧМ) — вид аналоговой модуляции, при котором информационный сигнал управляет частотой несущего колебания. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной. При частотной модуляции амплитуда несущего колебания U0 сохраняется постоянной, а частота несущего колебания ω(t) определяется модулирующим сигналом e(t) в соответствии с выражением: ω(t) = ω0 + kЧМ e(t) (1.15) где kЧМ - коэффициент пропорциональности, связывающий отклонение ΔωЧМ частоты ω(t) от своего номинального значения ω0, равное ΔωЧМ = ω(t) - ω0, и величину модулирующего напряжения e(t), вызывающего это отклонение. Максимальное отклонение частоты, вызываемое максимальным модулирующим напряжением, называют девиацией частоты. При модулирующем сигнале в виде гармонического напряжения e(t) = E cos(´Ωt+Θ) мгновенное значение частоты частотно-модулированного колебания изменяется по закону: ω(t) = ω0 + kЧМ E cos(´Ωt+Θ) (1.16) Временные диаграммы несущего и модулирующего колебаний, а также частотно-модулированного сигнала приведены на рисунке 1.5. (1.14) где n - число замеров. При восстановлении квантованной функции по Котельникову нужно знать все дискретные точки, как предыдущие, так и последующие, или во всяком случае для практической реализации должно быть известно несколько точек до и после интервала, в котором происходит интерполяция. Знание последующих точек возможно, лишь в системах, допускающих запаздывание в передаче информации. Большинство телемеханических систем работает в реальном масштабе времени и не допускает запаздывания. В таких системах приходится использовать ступенчатую интерполяцию, так как для линейной, нужно знать наперед хотя бы одну точку, что опять требует запаздывания. Действительно, если, например, известно значение функции в момент t4, т. 4), то при ступенчатой интерполяции нам заранее известно, что через ∆t значение функции будет тем же (т. 5`). Каким оно будет при линейной интерполяции через интервал ∆t, неизвестно: то ли значение возрастает (т. 5), то ли уменьшится (т. 52). Иногда восстановление функции, квантованной по времени, с шагом, подсчитанным по теореме Котельникова, производится при помощи фильтра НЧ, который выделяет постоянную составляющую и низкочастотные составляющие, соответствующие спектру передаваемой функции. Однако при этом возникают погрешности из-за того, что амплитудно-частотная характеристика реального фильтра отличается от характеристики идеального фильтра. Восстановление при помощи фильтра имеет смысл, если спектр передаваемой функции достаточно сосредоточен в области нуля по оси частот. Зачастую квантование по времени используется для осуществления амплитудно - импульсной модуляции. 1.7 Частотная модуляция Частотная модуляция (ЧМ) — вид аналоговой модуляции, при котором информационный сигнал управляет частотой несущего колебания. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной. При частотной модуляции амплитуда несущего колебания U0 сохраняется постоянной, а частота несущего колебания ω(t) определяется модулирующим сигналом e(t) в соответствии с выражением: ω(t) = ω0 + kЧМ e(t) (1.15) где kЧМ - коэффициент пропорциональности, связывающий отклонение ΔωЧМ частоты ω(t) от своего номинального значения ω0, равное ΔωЧМ = ω(t) - ω0, и величину модулирующего напряжения e(t), вызывающего это отклонение. Максимальное отклонение частоты, вызываемое максимальным модулирующим напряжением, называют девиацией частоты. При модулирующем сигнале в виде гармонического напряжения e(t) = E cos(´Ωt+Θ) мгновенное значение частоты частотно-модулированного колебания изменяется по закону: ω(t) = ω0 + kЧМ E cos(´Ωt+Θ) (1.16) Временные диаграммы несущего и модулирующего колебаний, а также частотно-модулированного сигнала приведены на рисунке 1.5. 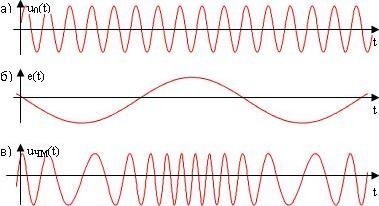 Рисунок 1.5 - Частотная модуляция: а) колебание с постоянной частотой; б) модулирующий сигнал; в) частотно-модулированное колебание Спектр сигнала при ЧМ очень широк, его полосу оценивают как 2(Δf + FB), что составляет 130-180 кГц. При модуляции чистым тоном с частотой F спектр радиосигнала содержит массу боковых частот fo ± nFB, где n = 1, 2, 3… (рисунке 1.6). При модуляции реальным звуковым сигналом спектр еще сложнее. Такие широкополосные сигналы можно разместить только на УКВ, поскольку, ввиду перегруженности низкочастотных диапазонов, там просто «не хватит места». В диапазоне же, например, 88-108 Мгц можно теоретически разместить до 100 каналов ЧМ вещания. Практически их меньше, и между соседними частотными каналами в одном населенном пункте стараются выдержать интервал не менее 400-500 кГц, учитывая несовершенство приемников. Рисунок 1.5 - Частотная модуляция: а) колебание с постоянной частотой; б) модулирующий сигнал; в) частотно-модулированное колебание Спектр сигнала при ЧМ очень широк, его полосу оценивают как 2(Δf + FB), что составляет 130-180 кГц. При модуляции чистым тоном с частотой F спектр радиосигнала содержит массу боковых частот fo ± nFB, где n = 1, 2, 3… (рисунке 1.6). При модуляции реальным звуковым сигналом спектр еще сложнее. Такие широкополосные сигналы можно разместить только на УКВ, поскольку, ввиду перегруженности низкочастотных диапазонов, там просто «не хватит места». В диапазоне же, например, 88-108 Мгц можно теоретически разместить до 100 каналов ЧМ вещания. Практически их меньше, и между соседними частотными каналами в одном населенном пункте стараются выдержать интервал не менее 400-500 кГц, учитывая несовершенство приемников. 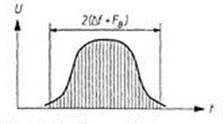 Рисунок 1.6 – Спектр ЧМ сигнала Высокое качество радиовещания с ЧМ объясняется не только широкой полосой звуковых частот. При демодуляции (детектировании) ЧМ сигнала происходит как бы обмен ширины спектра радиосигнала на отношение сигнал/шум на звуковой частоте. Помехи естественного и искусственного происхождения в УКВ диапазоне относительно невелики и хорошо подавляются приемником ЧМ сигналов. Все вместе взятое и обеспечивает высококачественный прием. Частотная модуляция применяется для высококачественной передачи звукового (низкочастотного) сигнала в радиовещании (в диапазоне УКВ), для звукового сопровождения телевизионных программ, передачи сигналов цветности в телевизионном стандарте SECAM, видеозаписи на магнитную ленту, музыкальных синтезаторах. Высокое качество кодирования аудиосигнала обусловлено тем, что при ЧМ применяется большая (по сравнению с шириной спектра сигнала АМ) девиация несущего сигнала, а в приёмной аппаратуре используют ограничитель амплитуды радиосигнала для ликвидации импульсных помех. Рисунок 1.6 – Спектр ЧМ сигнала Высокое качество радиовещания с ЧМ объясняется не только широкой полосой звуковых частот. При демодуляции (детектировании) ЧМ сигнала происходит как бы обмен ширины спектра радиосигнала на отношение сигнал/шум на звуковой частоте. Помехи естественного и искусственного происхождения в УКВ диапазоне относительно невелики и хорошо подавляются приемником ЧМ сигналов. Все вместе взятое и обеспечивает высококачественный прием. Частотная модуляция применяется для высококачественной передачи звукового (низкочастотного) сигнала в радиовещании (в диапазоне УКВ), для звукового сопровождения телевизионных программ, передачи сигналов цветности в телевизионном стандарте SECAM, видеозаписи на магнитную ленту, музыкальных синтезаторах. Высокое качество кодирования аудиосигнала обусловлено тем, что при ЧМ применяется большая (по сравнению с шириной спектра сигнала АМ) девиация несущего сигнала, а в приёмной аппаратуре используют ограничитель амплитуды радиосигнала для ликвидации импульсных помех. | |
2 РАСЧЕТНАЯ ЧАСТЬ
2.1 Расчет интервала дискретизации по теореме В.А.Котельникова и построение графика непрерывного сигнала
Задан сигнал Uн(ti)=(1-cosωti)e-ati . С частотой F=24 Гц, коэффициентом а=1, верхней граничной частотой Fв=30 Гц и периодом равным Тс=0,4 с и q=2.
Необходимо рассчитать интервал дискретизации по В.А. Котельникова:
Δt=1/2∙Fв, с
Δt=1/2∙30=0,017 с
Количество отсчетов:
N=T/t
N=0,4/0,017=23,53=23
Частоту:
ω=2∙3,14∙F, Гц
ω=2∙3,14∙24=150,72 Гц
Верхнюю частоту:
ωв=2∙3,14∙Fв, Гц
ωв=2∙3,14∙30=188,4, Гц
По формуле Uн(ti)=(q-cosωti)e-ati рассчитываются значения и записываются в таблицу 2.1
В качестве примера рассмотрим отсчет 10:
ti=k∙Δt=10∙0,0185=0,185 с
ω∙ti =100,48·0,185=18,6
cosωti = cos(18,6) = 0,947
q-cosωti = 3-0,947=2,053
e-ati = e-2·0,185 = 0,69
Uн(ti)=(q-cosωti)e-ati = 2,053·0,69=1,42 В
Аналогично данному примеру были выполнены расчеты остальных сигналов.
Таблица 2.1
