Алгебраический полном Лагранжа
Аппроксимация функций с помощью алгебраических интерполяционных полиномов
Данные, полученные при испытаниях сложных технических систем, для наглядности часто представляются графически, или в виде таблиц. Ввод сложных графиков, или таблиц большого объема в ЭВМ приводит к усложнению алгоритмов обработки. На практике предпочитают иметь дело не с графиком и таблицами, а с формулами. Если ошибки в экспериментальных данных можно не учитывать, то информацию, заданную графически или таблично, часто представляют с помощью интерполяционных формул. Простые и легко реализуемые на ЭВМ формулы дают алгебраические интерполяционные многочлены (алгебраические интерполяционные полиномы).
Задача аппроксимации функции с помощью алгебраического интерполяционного полинома формулируется следующим образом. Пусть аналитическое выражение функции Y=f(X) неизвестно, заданы только ее значения Y1,...,YN в точках X1,...XN некоторого отрезка [a,b]. Необходимо найти полином степени n
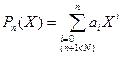 ,
, 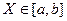 , (2.1)
, (2.1)
для которого выполняются условия:
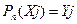 ,
, 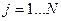 , (2.2)
, (2.2)
Так как в точках Xj значения функции Yj и значения полинома Pn (Xj) должны совпадать между собой, то неизвестные коэффициенты полинома можно найти путем решения системы уравнений (2.2)
Когда n+1<N, система (2.2) не имеет решений. Если среди узлов Xj нет совпадающих между собой точек, то система линейных алгебраических уравнений (2.2) может иметь единственное решен  ие только при n+1=N, т.е. n=N-1, т.к. определителем этой системы является определитель Вандермонда, имеющий вид:
ие только при n+1=N, т.е. n=N-1, т.к. определителем этой системы является определитель Вандермонда, имеющий вид:
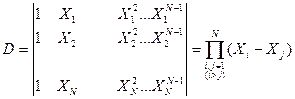 , (2.3)
, (2.3)
Известно, что при различных Xj этот определитель отличен от нуля, т.е. система уравнений имеет решение.
По заданным N парам чисел (Xj,Yj) j=1,...N можно найти полином степени (N-1). Этот полином является единственным.
Интерполяционная формула Лагранжа
Одну из простейших формул интерполяции позволяет построить метод Лагранжа. По условию находим полином PN-1(X) степени (N-1), который в N точках совпадает с N значениями функции f(X). Если найти систему полиномов í jj(X)ý, каждый из которых в точке Xj равен 1, а в остальных точках равен нулю, то интерполяционный полином можно представить в виде:
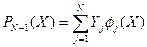 , (2.4)
, (2.4)
Это следует из того, что
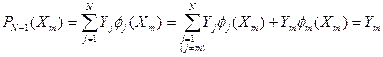
Последовательность функций íjj (X)ý такого типа называется фундаментальной системой полиномов.
По предположению полином jj(X) в точках Xk, при k¹j обращается в нуль. поэтому его можно представить в виде:
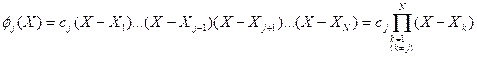 , (2.5)
, (2.5)
где Cj-некоторая постоянная.
Учитывая, что jj(Xj)=1, пол  учим:
учим:
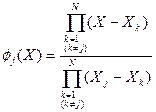 , (2.6)
, (2.6)
Отсюда следует, что интерполяционный полином Лагранжа имеет вид
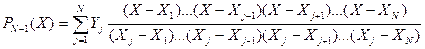 , (2.7)
, (2.7)
