Уровни исследования информации
· Технический (синтаксический) – он
отображает формально-структурные
характеристики информации и не
затрагивает ее смыслового содержания. На
этом уровне учитывается тип носителя и
ппооссообб ппррееддссттааввллеенниияя ииннффооррммааццииии,,
скорость передачи и обработки, размеры кодов представления информации,
надежность и точность преобразования
этих кодов и т.п.
· Информацию, рассматриваемую только с
технических позиций, обычно называют
данными, так как при этом не затрагивается
смысловая сторона.
Уровни исследования информации
· Семантический (смысловой) – на этом уровне определяется степень соответствияобраза объекта и самого объекта. Семантический аспект предполагает учет
ммыыссллооввооггоо ссооддеерржжаанниияя ииннффооррммааццииии.. ННаа этом уровне анализируются те сведения, которые отражает информация, рассматриваются смысловые связи. На этом уровне формируют понятия и представления, выявляют смысл, содержание информации и ее обобщение.
Уровни исследования информации
· Прагматический (потребительский) – на этом уровне исследуют отношениеинформации и ее потребителя, соответствие информации цели управления, которая на ее
ссннооввее ррееааллииззууееттссяя..
· Прагматический аспект рассмотрения связан с ценностью, полезностью использования информации при выработке потребителем решения для достижения своей цели. С этой точки зрения анализируются потребительские свойства информации.
Количество информации
В науке понятие информации введено в 1928 г. американским инженером Хартли для обозначения меры количественногоизмерения сведений. Для вычисления количества информации как меры неопределенности (устраняемой в результате получения информации) Хартли предложил логарифм по основанию два:
 I = log2N
I = log2N
де I количество информации, N - число возможных состояний объекта.
Если объект пребывает только в 2 состояниях (N = 2), они кодируются двоичным кодом - 0 или 1, тогда I = 1.
Так определяется единица информации – бит. Бит – единица информации, позволяющая сохранить «одно из двух»: либо «да», либо «нет».
Энтропия системы
Исследованием в сфере информации успешно занимался К. Шеннона.
Постановка задачи:
Пусть у окончивших институт есть 4 варианта (исхода) дальнейшего развития событий:
· устроиться на работу, · пойти учиться дальше, · пойти в армию,
· ничего не делать.
Каждый исход имеет вероятность осуществления. Очевидно, что сумма вероятностей будет равна 1.
Мера неопределенности. Известно, как распределялись окончившие институт в прошлые годы, но как сложатся пропорции в этом году, неизвестно, поэтому состоянию выборки присуща некоторая неопределенность. Можно ли измерить неопределенность?
В общем случае выборка может включать различное количество возможных исходов (k).
При k=1 исход предопределен: неопределенность равна нулю.
При к=2 неопределенность отлична от нуля, поскольку оояяввлляяееттссяя ввооззммоожжннооссттьь ввыыббоорраа..
С увеличением числа возможных исходов (k) неопределенность 6yдет расти.
Следовательно, меру неопределенности рассматривать как функцию от числа исходов – f(k).
Можно возможных
Таким образом, в любой системе сложность, разнообразие ее зависят от количества различимых элементов, числа их возможных состояний и количества связей между ними.
· Мера неопределенности системы Н(a), имеющая N возможных состояний, согласно формуле Шеннона, равна:
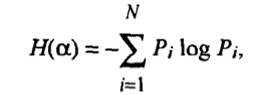
|
· Величину Н, являющуюся мерой неопределенности события (явления, процесса), К. Шеннон назвал энтропией.
