Понятие и свойства канонического расписания реального времени
Пусть имеем R различных приоритетов абонентов в системе, обслуживаемых по расписанию, соответственно 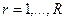
 , и
, и 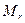 абонентов системы имеют равный r приоритет
абонентов системы имеют равный r приоритет 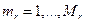 :
: 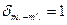 ,
, 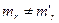 ,
, 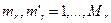 . Таким образом система содержит M абонентов, которым соответствует R уровней приоритетов.
. Таким образом система содержит M абонентов, которым соответствует R уровней приоритетов.
Детерминированная задача синтеза расписаний реального времени может быть сформулирована следующим образом : 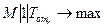 ,
, 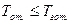 ,
, 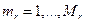 ,
, 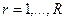 , где
, где 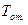 - характеристика обслуживания m-го абонента r-го приоритета,
- характеристика обслуживания m-го абонента r-го приоритета, 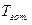 - ограничение, накладываемое на время обслуживания заявки абонента системой, функционирующей в реальном масштабе времени.
- ограничение, накладываемое на время обслуживания заявки абонента системой, функционирующей в реальном масштабе времени.
С учетом сформулированной задачи синтеза расписаний реального времени дадим определение канонического (в данном случае - оптимального) расписания. Под каноническим расписанием будем понимать расписание, обеспечивающее минимальные значения характеристик 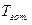 в рамках заданного разбиения M абонентов на R уровней приоритета, получаемое поочередной передачей прав абонентам в рамках радиального графа.
в рамках заданного разбиения M абонентов на R уровней приоритета, получаемое поочередной передачей прав абонентам в рамках радиального графа.
Под радиальным графом передачи прав понимается граф, содержащий 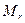 вершин приоритета r,
вершин приоритета r, 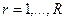 , причем в каждую вершину нижестоящего приоритета входит только одна дуга от одной вершины вышестоящего приоритета, из каждой вершины всех приоритетов, кроме R-го выходит [
, причем в каждую вершину нижестоящего приоритета входит только одна дуга от одной вершины вышестоящего приоритета, из каждой вершины всех приоритетов, кроме R-го выходит [ 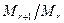 ] дуг, где [a] - есть большее целое числа a, все вершины приоритета R соединяются дугой с вершиной приоритета 1 (из вершин R выходит только одна дуга) - в этом случае дуга направлена в сторону вершины 1, в то время как в остальных случаях дуга направлена в вершину, соответствующую пользователю с более низким приоритетом. Радиальный граф передачи прав представлен на рис. 2.15.
] дуг, где [a] - есть большее целое числа a, все вершины приоритета R соединяются дугой с вершиной приоритета 1 (из вершин R выходит только одна дуга) - в этом случае дуга направлена в сторону вершины 1, в то время как в остальных случаях дуга направлена в вершину, соответствующую пользователю с более низким приоритетом. Радиальный граф передачи прав представлен на рис. 2.15.
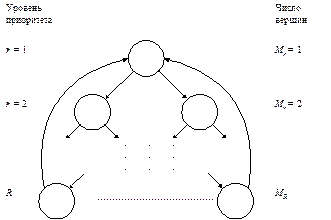
Рис. 2.15
Радиальный граф, у которого по крайней мере одна вершина r-го (не R-го) уровня приоритета соединена только с одной вершиной приоритета уровня 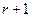 назовем вырожденным. Соединение двух вершин одной дугой является альтернативным способом задания равного приоритета двум абонентам системы. Под предельно вырожденным понимаем граф, в котором из каждой вершины только одна дуга выходит и в каждую вершину только одна дуга входит - этот граф задает бесприоритетное расписание, соответствующее обслуживанию в циклическом порядке.
назовем вырожденным. Соединение двух вершин одной дугой является альтернативным способом задания равного приоритета двум абонентам системы. Под предельно вырожденным понимаем граф, в котором из каждой вершины только одна дуга выходит и в каждую вершину только одна дуга входит - этот граф задает бесприоритетное расписание, соответствующее обслуживанию в циклическом порядке.
Под поочередной будем понимать такую передачу прав на занятие ресурса абонентами, при которой абоненты одного приоритета получают полномочия на доступ к ресурсу с равной частотой или бесприоритетно друг относительно друга. Для радиального графа такая очередность может быть определена в результате выполнения следующей итерационной процедуры. В общем случае реализуется R итераций.
1. Произвольным образом через одну вершину каждого приоритета проводится первый путь.
2. Второй путь должен пройти через вершины всех приоритетов, кроме первого(через первый путь проходит всегда), не соединенные первым путем, третий, не соединенные первыми двумя путями и т.д.
3. Если не осталось на рассмотрении вершин r -го приоритета через которые не прошел по крайней мере один путь (для невырожденного графа прежде всего это приоритет 2) из проведенных r путей (2 путей), 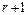 дуга проходит как и первая, но уже через другие вершины приоритета
дуга проходит как и первая, но уже через другие вершины приоритета 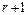 и т.д., вплоть до соединения путями вершины первого приоритета со всеми вершинами приоритета R.
и т.д., вплоть до соединения путями вершины первого приоритета со всеми вершинами приоритета R.
4. Все вершины R приоритета соединяются дугой с вершиной высшего приоритета.
5. Нумеруются пути в соответствии с очередностью их получения. Именно в соответствии с этой нумерацией (с этим порядком) в системе должны передаваться полномочия на доступ к ресурсу.
6. Для каждого полученного пути определяется очередность передачи полномочий между вершинами графа (абонентами) перечислением очередности появления соответствующих вершин на пути.
Иллюстрация получения поочередной передачи прав, с использованием приведенной процедуры представлена на рис. 2.16.
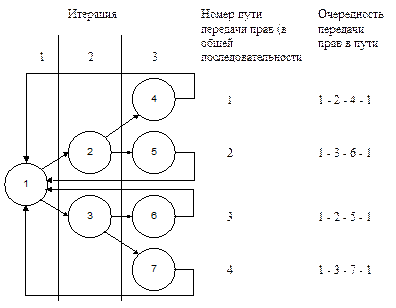
Рис. 2.16
Свойства канонических расписаний реального времени.
1. В общем случае для каждого абонента в системе в цикле расписания может быть несколько очередностей передачи прав на доступ к ресурсу 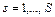 , например, (1, 2, 1, 3, 4). Тогда параметры обслуживания заявок абонента определяются гарантированной продолжительностью обслуживания
, например, (1, 2, 1, 3, 4). Тогда параметры обслуживания заявок абонента определяются гарантированной продолжительностью обслуживания 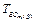
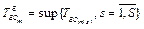 ,
,
и средней продолжительностью гарантированного обслуживания требований с учетом различных очередностей S
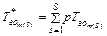 .
.
Таким образом в общем случае - при нескольких очередностях в системе дисциплина обслуживания реального времени задается параметрами 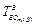 и
и 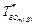 . Для канонического расписания значения
. Для канонического расписания значения 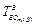 и
и 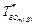 соответственно совпадают для абонентов всех R приоритетов.
соответственно совпадают для абонентов всех R приоритетов.
2. В системе реализуются минимально возможные значения 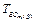 для всех
для всех 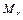 абонентов всех R приоритетов.
абонентов всех R приоритетов.
3. Относительный уровень (коэффициент) приоритетности абонентов 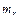 ,
, 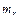 :
: 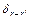 вырожденного графа - при минимальных
вырожденного графа - при минимальных 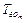 составляет
составляет
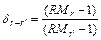 ,
,
соответственно, ограничением на общность построения радиального графа будет
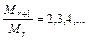 ;
; 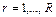
Из анализа свойств канонических расписаний, можем сделать следующие выводы.
1. В основе синтеза расписаний реального времени должно находиться построение канонического расписания, с последующей его модификацией, учитывающей особенности конкретной задачи синтеза.
2. При минимизации значений параметра 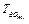 для всех абонентов всех уровней приоритета системы R (эффективное использование ресурса) строго задается соотношение уровней коэффициента приоритетности абонентов системы.
для всех абонентов всех уровней приоритета системы R (эффективное использование ресурса) строго задается соотношение уровней коэффициента приоритетности абонентов системы.
3. Исходное соотношение коэффициентов приоритетности может быть изменено либо подбором соответствующих значений двух других параметров 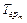 и
и 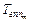 в рамках канонического расписания, либо изменением значений
в рамках канонического расписания, либо изменением значений 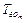 (либо
(либо 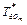 , в общем случае они могут не совпадать), путем их увеличения (уменьшить их уже невозможно, что следует из второго свойства канонических расписаний) для абонентов отдельных уровней приоритета.
, в общем случае они могут не совпадать), путем их увеличения (уменьшить их уже невозможно, что следует из второго свойства канонических расписаний) для абонентов отдельных уровней приоритета.
Аналогично может быть построено расписание и для ЛВС ОО. Следует отметить, что в этом случае расписание также может синтезироваться по параметрам 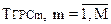 . При этом значения
. При этом значения 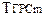 должны выбираться таким образом, чтобы для синтезированного по этим параметрам расписания выполнялось:
должны выбираться таким образом, чтобы для синтезированного по этим параметрам расписания выполнялось: 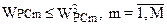 .
.
Методика синтеза расписания в данном случае состоит в следующем.
1.Назначаются 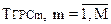 , где
, где 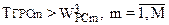 .
.
2.Для заданных параметров 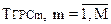 с использованием описанной выше методики синтезируется расписание
с использованием описанной выше методики синтезируется расписание
3.Строится модель (аналитическая или имитационная) системы массового обслуживания с полученным расписанием с целью определения значений 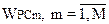 .
.
4.Проводится сравнение значений 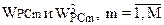 . В результате которого значения уменьшаются для тех параметров m для которых
. В результате которого значения уменьшаются для тех параметров m для которых 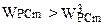 соответственно увеличиваются в случае, если
соответственно увеличиваются в случае, если 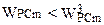 .
.
5.С новыми заданными значениями 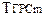 переход к п.п.2.
переход к п.п.2.
Синтез расписания продолжается до выполнения условия: 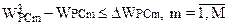 ,
,
где значения 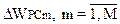 задаются перед началом решения задачи, исходя из условий задачи.
задаются перед началом решения задачи, исходя из условий задачи.
Замечание. Задача синтеза расписания для ЛВС ОО может решаться и за один этап, однако это требует решения задачи определения значения 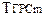
для заданного 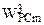 т.е. должны быть определены и формализованы зависимости
т.е. должны быть определены и формализованы зависимости 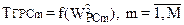 .
.
Данная задача на сегодняшний день не решена и в книге лишь обозначается в постановочной части.
