Криптография. алгоритм rsa

Суть со­сто­ит в том, что ка­ж­дым ад­ре­са­том ИС ге­не­ри­ру­ют­ся два клю­ча, связан­ные ме­ж­ду со­бой по оп­ре­де­лен­но­му пра­ви­лу. Один ключ объ­яв­ля­ет­ся откры­тым, а дру­гой за­кры­тым. От­кры­тый ключ пуб­ли­ку­ет­ся и дос­ту­пен лю­бо­му, кто же­ла­ет по­слать со­об­ще­ние ад­ре­са­ту. Секретный ключ сохраняется в тайне.

Ис­ход­ный текст шиф­ру­ет­ся от­кры­тым клю­чом адресата и пе­ре­да­ет­ся ему. За­шиф­ро­ван­ный текст в прин­ци­пе не мо­жет быть рас­шиф­ро­ван тем же от­кры­тым клю­чом. Де­шиф­ро­ва­ние со­об­ще­ние воз­мож­но толь­ко с ис­поль­зо­ва­ни­ем за­кры­то­го клю­ча, ко­то­рый из­вес­тен толь­ко са­мо­му ад­ре­са­ту.

Ри­ве­ст, Ша­ми­р и Эй­дель­ма­н вос­поль­зо­ва­лись тем фак­том, что на­хо­ж­де­ние боль­ших про­стых чи­сел в вы­чис­ли­тель­ном от­но­ше­нии осу­ще­ст­в­ля­ет­ся лег­ко, но раз­ло­же­ние на мно­жи­те­ли про­из­ве­де­ния двух та­ких чи­сел прак­ти­че­ски не­вы­пол­ни­мо. До­ка­за­но (тео­ре­ма Ра­би­на), что рас­кры­тие шиф­ра RSA эк­ви­ва­лент­но та­ко­му раз­ло­же­нию. По­это­му для лю­бой дли­ны клю­ча мож­но дать ниж­нюю оцен­ку чис­ла опе­ра­ций для рас­кры­тия шиф­ра, а с уче­том про­из­во­ди­тель­но­сти со­вре­мен­ных ком­пь­ю­те­ров оце­нить и не­об­хо­ди­мое на это вре­мя.

RSA на примере:

Выбираем два простые числа p=7; q=17 (на практике они во много раз длиннее!!!)

В этом случае N = p*q будет равно 119.

Функция Эйлера K = (p-1)*(q-1) = 96

Теперь необходимо выбрать случайное e, взаимно простое сn ,выбираем e=5.

Сформируем число d так, чтобы (d*e) mod K = 1

(5*d) % 96 = 1 à d = 77

d – секретный ключ, e и n – характеризуют открытый ключ.

Текст, который нужно шифровать M = 19

Получаем зашифрованный текст С = M^e mod n = 66

Получатель дешифрует сообщение М= C^d mod n =19

Двоичные коды с обнаружением и коррекцией одиночных ошибок. Графическая интерпретация.

Пример обнаружения ошибочного разряда в коде Хемминга

Дано кодовое слово (КС): 0 1 0 1 1 0 1 (0 1 0 1 – данные, 101 – синдром)

Пусть при передаче произошла ошибка, и оно исказилось: 0 1 0 1 1 0 0

Необходимо выполнить проверку на корректность и исправить ошибку, если она есть.

Перемножаем матрицу Н на столбец КС (по правилу строка на столбец), получаем код ошибки:

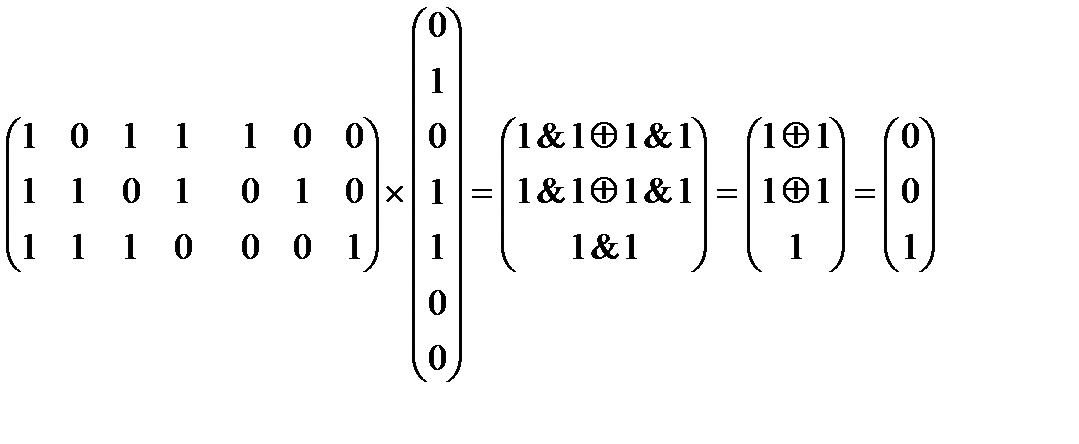
упрощенно:

>

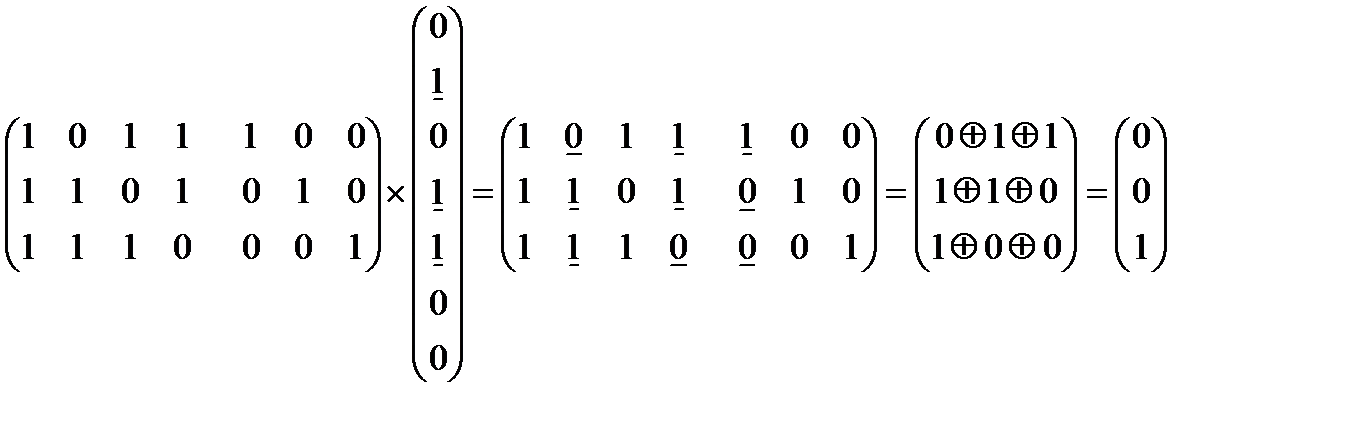
Поскольку получен код, отличный от безошибочного {0 0 0},

ищем соответствующий ему столбец в матрице H.

Как наглядно видно – это крайний справа.

Исправляем ошибку и записываем ответ: 0 1 0 1 1 0 0 → 0 1 0 1 1 0 1

Коды Хемминга. Помехоустойчивость. Схема авто коррекции данных.

В другом файле.

Коды Хемминга для разной длины кодовых слов.

В другом файле.

Фонетические алфавиты. Алфавит ИКАО/ICAO.

Фонетический алфавит международной авиационной организации (ИКАО), также известный как международный радиотелефонный алфавит, или просто "радиоалфавит" — один из самых распространённых фонетических алфавитов в мире. Каждой букве он ставит в соответствие определённое кодовое слово (A как Alfa, B как Bravo, и т.д.) таким образом, чтобы последовательности букв (и цифр) могли быть легко произнесены и правильно поняты при голосовом общении по радио или телефону, независимо от родного языка передающей/принимающей стороны. Фонетический алфавит ИКАО используется многими международными и национальными организациями.

Реализация составных операций в языке Ассемблер. Условный оператор в полном и сокращенном (одна ветвь) виде.

CMP AX, BX ; анализирует разность (AX - BX), устанавливает флаги FZ и FS

; флаг знаков: FS = 0 если AX-BX≥0, FS = 1 если AX-BX<0 (0 – ”+”, 1 – ”-”)

; флаг значений: FZ = 0 если AX≠BX, FZ = 1 если AX=BX (разность = или ≠ 0)

Примечание: команды TEST и CMP только меняют флаги, значения операндов остаются прежними!

Передача управления (безусловный и условный переход):

METKA1: ........

JMP METKA1 ; безусловный переход к указанной метке (вверх или вниз)

Переход по условию:

JS METKA ; переход происходит, если FS = 1 (буква Sв имени команды – указывает флаг)

JNS METKA ; переход происходит, если FS = 0 (буква Nв имени команды – как бы отрицание)

JZ METKA ; переход происходит, если FZ = 1 (буква Zв имени команды – указывает флаг)

JNZ METKA ; переход происходит, если FZ = 0 (буква Nв имени команды – как бы отрицание)