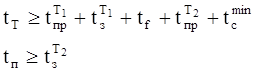Реализация автоматов Мили с задержкой

Введение в контур автоматов автомата

Мура позволяет устранить "порочную

петлю", так как у него

Y(t) = F(S(t)) и \ Y(t) ¹ f(X(t))

Тот же эффект дает автомат Мили с за- держкой, у которого

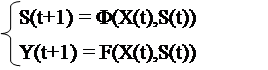и \ Y(t) ¹ f(X(t)).

Y(0) можно определять произвольно

Автоматы Мили с задержкой при одина-

ковом числе состояний с автоматами

Мура могут иметь большее разнообразие

реакций, так как у них Y=F(X,S), а не Y = F(S).

Благодаря этому автоматы Мили с за- держкой имеют меньшее число состоя- ний чем эквивалентные автоматы Мура, что выгодно, ибо сокращает число аргу- ментов функций переходов структурно

го автомата.

Реализовать автомат Мили с задержкой можно по-разному.

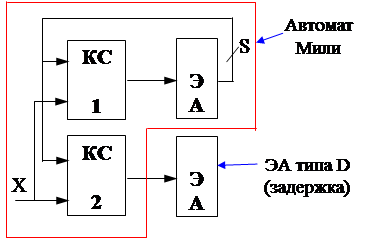Эту схему можно рассматривать как автомат с тактом на спаде С.

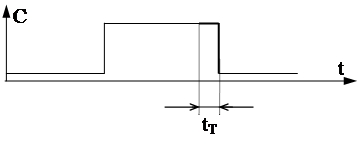В это время S и Y не меняются , а значение Х

определит S(t+1) и Y(t+1).

При этом время паузы t_п получится как

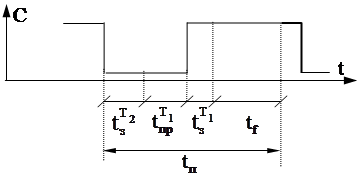Можно трактовать такт и иначе: при С=1, но тогда время такта будет больше.

При этом растет требуемое время для со-хранения Х неизменным.

Триггеры для Х могут быть не нужны,

если на вход схемы подаются сигналы,
не меняющиеся во время С=0. (Мы по-

лучим схему с непересекающимися вход-

ным микротактом t¹ и выходным - t⁰.) Та-

кое часто бывает.

Тогда возможна схема

В заключение отметим, что в этой схеме триггеры ТТ1 могут быть заменены на

триггеры с динамической синхронизаци-

ей по фронту. (Триггеры Т2 тоже могут

быть с динамической синхронизацией,

но по спаду.)

Неканонические

Автоматы Мили.

Каноническая реализация автоматов

Мили нам известна

Однако в ряде случаев важных для прак- тики, мы можем строить схемы проще.

Речь идет о неканонических автоматах Мили

с (t¹ Ç t⁰) = Æ и с устойчивыми переходами и выходами при которых

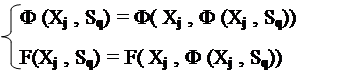Такие автоматы часто встречаются,

особенно в составе операционных авто-

матов. Таков, например, операционный

элемент регистр, предназначенный для

приема и хранения информации.

Реализуя такие автоматы, можно не бес-покоиться о том, чтобы смена состояния не происходила во время такта, ибо она не пов-

лияет на поведение автомата.

Типичная реализация такова

ЭА на основе " обычных "

одноступенчатых триггеров.

Постоянство Х в t¹ обеспечивает внеш-

няя среда, постоянство Y в t⁰ - схема.

Неканонические автоматы А₁ и А₂ не

могут обмениваться сигналами, если у

них одна тактность. Если же t₁⁰ = t₂¹ и
t₁¹ = t₂⁰, то обмен возможен. Именно так построена двухступенчатая триггерная

схема ЭА Мура.

4.4.Установка начального

состояния автомата.

Мы имеем дело с инициальными автома- тами - автоматами с известным состояни- ем S(0).

Для них S(0) должно быть установлено до того, как начнется интервал времени, соответствующий такту t=0.

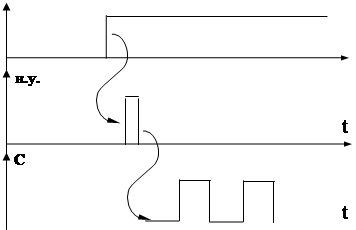
В триггерных моделях ЭА такая уста-

новка выполняется с помощью входов

асинхронной установки, воспринимаю-

их сигналы в отсутствии синхросигна-

лов.

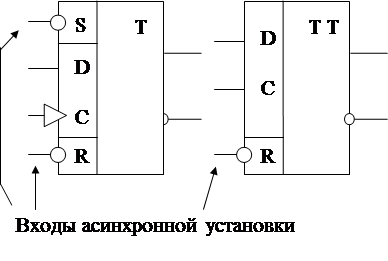Пример

t

Работа автомата

Установка S(0) идет до появления (включения) синхросерии.

503

Часто ЭА проще устанавливать в Q(0) =
= 0, чем в Q(0) = 1. При этом, кодируя
состояния, предпочитают брать S(0) =

= 00...0.

4.5. Автономные автоматы.

Автономным называется автомат Мура вида:

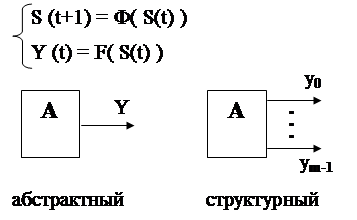Отсутствие в качестве аргумента Х обу- славливает однозначность перехода из любого состояния. Функции переходов автономного автомата могут иметь один

из следующих видов:

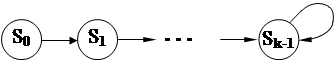
1)

2)

3)

Автоматы вида 1) "генерируют" перио- дическую последовательность выходных сигналов с периодом К.

(Последовательность сигналов в периоде определяется тем, как отмечены выход ными сигналами различные состояния.)

Пример

Имеем бесконечную последовательность

00101 00101 ...00101...

Она может формироваться автоматом вида

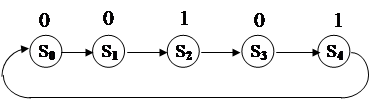Автоматы вида 2) "генерируют" перио-

дическую последовательность выходных сигналов, которую предваряет последо-

вательность конечной длины.

Пример

Имеем последовательность

01.01.00.10.01 ... 00.10.01 ...

(точками разделены одновременные сиг- налы 2^х выходов.) Последовательность может формироваться автоматом вида:

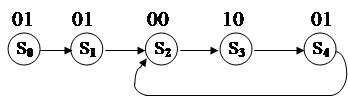Автоматы вида 3) "генерируют" последова-тельность выходных сигналов, начинающую-

ся произвольной последовательностью длины

(К-1) и продолжающуюся бесконечным повто-рением одинаковых сигналов, соответствую-

щих S_{к -1} .

Найдя периодическую часть некоторой последовательности и, возможно, пред-варяющую период последовательность

конечной длины, мы можем построить

функции переходов и выходов реали-

зующего ее автомата.

Функции выходов могут быть любыми,

причем от них в сильной мере будет за-

висеть возможный вид структурного ав-

томата ( его внутренняя композиция ).

Основываясь на разных методах коди-

рования состояний (см.2.3.), можно полу-

чать схемы разного вид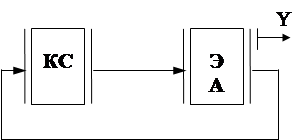а:

а)

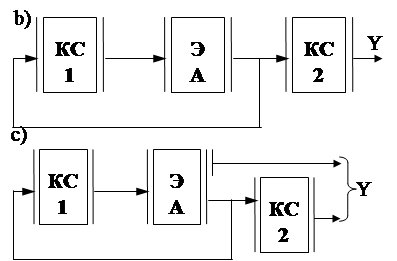
Синтез схем вида а) и с) ничем не отличается от синтеза автоматов со входами

Пример схемы вида а)

Дано:

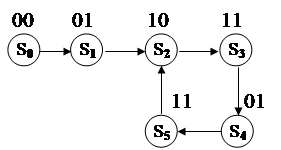Кодируя получим:

S₂ =100 ; S₃ =110 ; S₄ =010 ;

S₅ =111 ; S₁ =011 ; S₀ =001 ;

(См. раздел 2.3)

Отсюда получаем кодированную таблицу переходов. Взяв ЭА типа JK построим функции возбуждения, а затем всю схему.

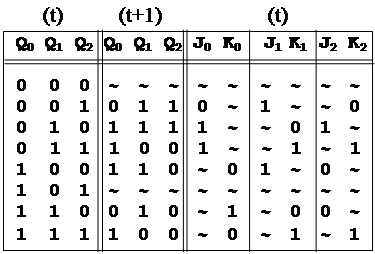
Отсюда получим:

J₀ = Q₁ ; K₀ = Q_{1 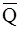2} ;

J₁ = “1” ; K₁ = Q₂ ;

J₂ = 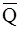₀ ; K₂ = Q₁ ;

В итоге схема содержит 3 ЭА типа JK и конъюнктор для реализации K₀ = Q_{1 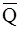2}

Схемы вида b)

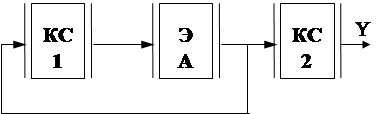Строятся, если можно взять в качестве основы ЭА с большим числом состояний, содержащий цепочку состояний S₀ , S₁, ... S_k-1 с переходами по одинаковым условиям.

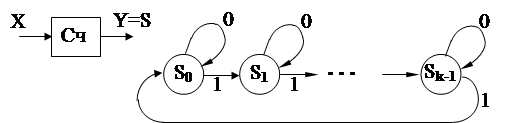
Такие ЭА обеспечивают простоту реализации функций переходов автономного автомата. В качестве примера такого ЭА можно взять aв-томат, реализующий функцию счета - счетчик.

Счетчик, воспринимая Х=1, переходить от S_i к S_i+1, а при Х=0 переходит от S_i к S_i . Все состо-яния счетчика однозначно представляются вы-ходными сигналами (Y = S ).

набор ЭА с двумя состояниями

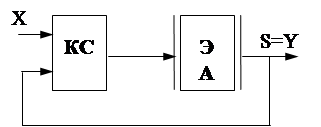Внутренняя структура счетчика таков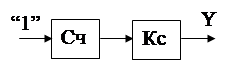а

Используя счетчик, легко построить схему авто-номного автомата с функциями переходов вида

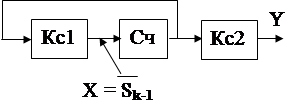Счетчики представляют собой специфи-

ческие, но широко употребимые схемы,

которые почти всегда имеются в наборе технических средств , используемых для

синтеза композиций. Построение схем

счетчиков изучается схемотехникой.

К особенностям схем относится возмож-

ность организации их работы в режиме

счета по модулю К (кольцевой счет от 0

до (К-1) и наоборот) при любых К.

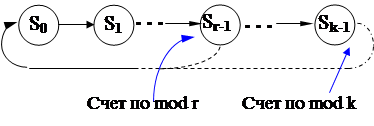
Часто схемы счетчиков допускают орга-

низацию работы с переходами вида

Взяв счетчик с функцией переходов того же вида, что у строящегося автономного автомата, можно получать автономные автоматы как:

Синтез синхронных УА