Предварительные сведения

Лабораторная работа № 3

Синтез схемы шифратора и дешифратора для управления

Разрядным 7-сегментным индикатором

ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ

Проиллюстрируем методику решения задачи построения шифратора и дешифратора.

1. Входные данные вводятся в унитарном коде. Унитарный код двоичного n-разрядного числа представляется 2n разрядами, только один из которых равен 1. Для преобразования этого кода в двоичный код следует применить шифратор. Шифратор должен иметь десять входов, каждому из которых соответствует одно из чисел 0, 1, 2,...,9. Число 9 в двоичном коде представляется разрядами: 1001, т.е. шифратор должен иметь четыре выхода. В соответствии с этими требованиями составляют таблицу истинности (табл.1).

Таблица 1

Таблица истинности шифратора

№

Входныепеременные

Выходные переменные

пп

x0

x1

x2

x3

x4

x5

x6

x7

x8

x9

y1

y2

y3

y4

2. Получают логическую функцию шифратора в виде СДНФ путем записи “по единицам” (табл.1):

y1=x8+x9;

y2=x4+x5+x6+x7;

y3=x2+x3+x6+x7;

y4=x1+x3+x5+x7+x9

3. Используя полученные уравнения можно синтезировать функциональную схему шифратора в логическом базисе И, ИЛИ, НЕ (рис.1):

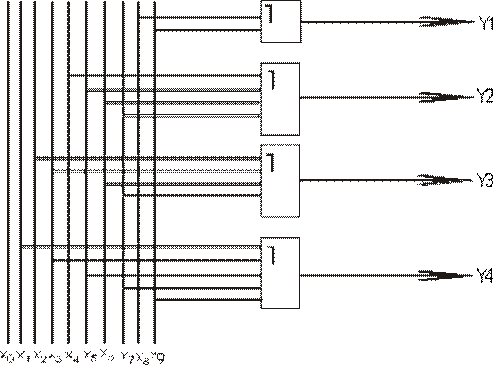
Рис.1. Функциональная схема шифратора на логических элементах или для синтеза шифратора в логических базисах И-НЕ или ИЛИ-НЕ следует применить закон двойной инверсии и закон инверсии (закон Де Моргана):

После выбора из табл.4 микросхем синтезируют принципиальную электрическую схему шифратора в заданном табл.5 базисе.

4. Допустим, что последние четыре цифры номера зачетной книжки образуют число 3011, т.е. должны индицироваться только стилизованные цифры 0, 1, 3, а при вводе остальных цифр - символ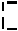

5. При составлении таблицы истинности кодопреобразователя (табл.2) учитывают, что входные данные вводятся в двоичном коде, а наличие высокого потенциала на выходах кодопреобразователя y1, y2, y3,..., y7 вызывает свечение соответственно сегмента a, b, c, d, e, f, g 7-сегментного индикатора.

Таблица 2

Таблица истинности кодопреобразователя

№	Входные	Выходные переменные
пп	переменные	a	b	c	d	e	f	g
	x4	x3	x2	x1	y1	y2	y3	y4	y5	y6	y7
10. .15	х	х	х	х	х	х	х

Символом “х” в табл. 2 обозначены безразличные состояния выходных переменных.

6. Для нахождения МДНФ применяют диаграммы Вейча-Карно (рис.2). Из табл.2 видно, что y1=y4; y2=y3; y5=y6.

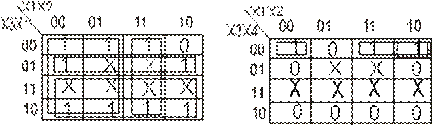
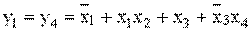
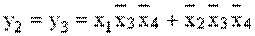
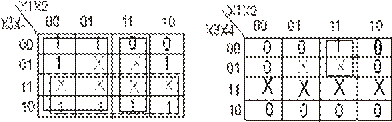
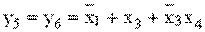
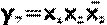
Рис.2. Диаграммы Вейча-Карно для кодопреобразователя

На диаграммах Вейча-Карно безразличные состояния входных переменных, отмеченные символом “х” и включенные в контуры, считаются единичными, а вне контуров – нулевыми.

7. Для реализации функциональной схемы в базисе И-НЕ преобразуют полученные МДНФ, применяя законы двойной инверсии и инверсии (закон Де Моргана):

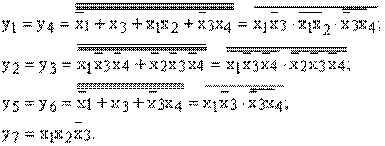
8. Для реализации функциональной схемы в базисе ИЛИ-НЕ преобразуют полученные МДНФ, применив указанные законы:

9. Схема кодопреобразователя в логическом базисе И, ИЛИ, НЕ (рис.3):

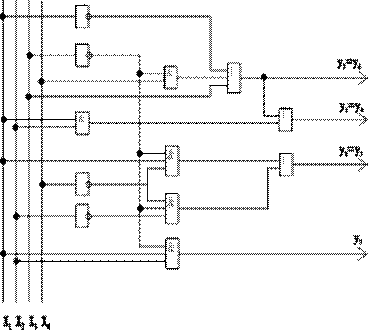
Рис.3. Функциональная схема кодопреобразователя в логическом базисе И, ИЛИ, НЕ

10. Схема кодопреобразователя в логическом базисе И-НЕ на логических элементах типа К176ЛА7 и К176ЛА9 (рис.4):

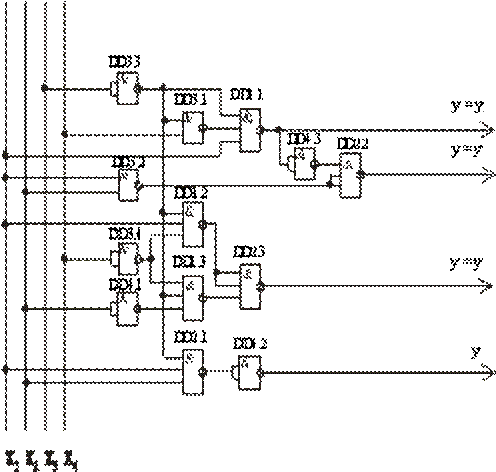
DD1, DD2: K176ЛА9 - 3х3 И-НЕ

DD3, DD4: K176ЛА7 - 4х2 И-НЕ

Рис.4. Принципиальная электрическая схема кодопреобразователя

в логическом базисе И-НЕ

11. Так как между входом x3 и выходом y1 включено 5 логических элементов, то задержка кодопреобразователя равна

tз=5 tз.ср=5(200...300) =(1000...1500) нс.

12. Схема кодопреобразователя в логическом базисе ИЛИ-НЕ на логических элементах типа К176ЛЕ5 и К176ЛЕ10 (рис.5):

DD1 – DD4: K176ЛЕ5 - 4х2 ИЛИ-НЕ

DD5: K176ЛЕ10 - 3х3 ИЛИ-НЕ

Рис.5. Принципиальная электрическая схема кодопреобразователя в логическом базисе ИЛИ-НЕ

13. Так как между входом x1 и выходом y1 включено 7 логических элементов, то задержка кодопреобразователя равна

tз=7(200...300) =(1400...2100) нс.