Методические указания. 1. К пункту 5 задания для подготовки

1. К пункту 5 задания для подготовки.

Частотная характеристика «приподнятого косинуса» имеет вид: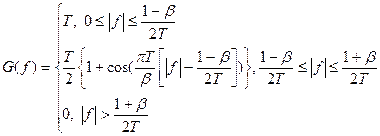

мкс.

2. К пункту 6 задания для подготовки.

Комплексная модель низкочастотного эквивалента сигнала ФМ-2, прошедшего канал связи, имеет вид:

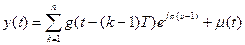, , , - дискретная случайная величина, принимающая два возможных значения 0 или 1 с равными вероятностями 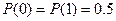, 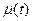-комплексный стационарный гауссовский шум.

2. К пункту 7 задания для подготовки.

Блок-схема алгоритма (6):

M-количество реализаций.

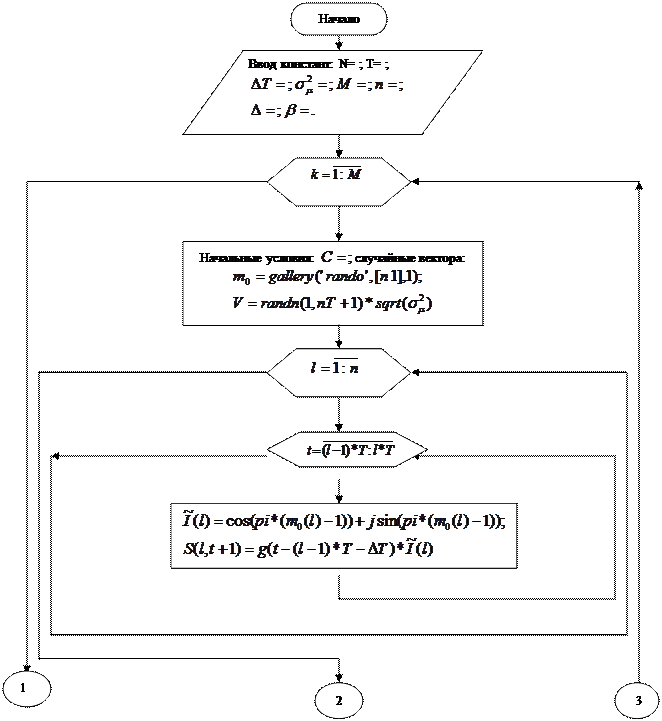
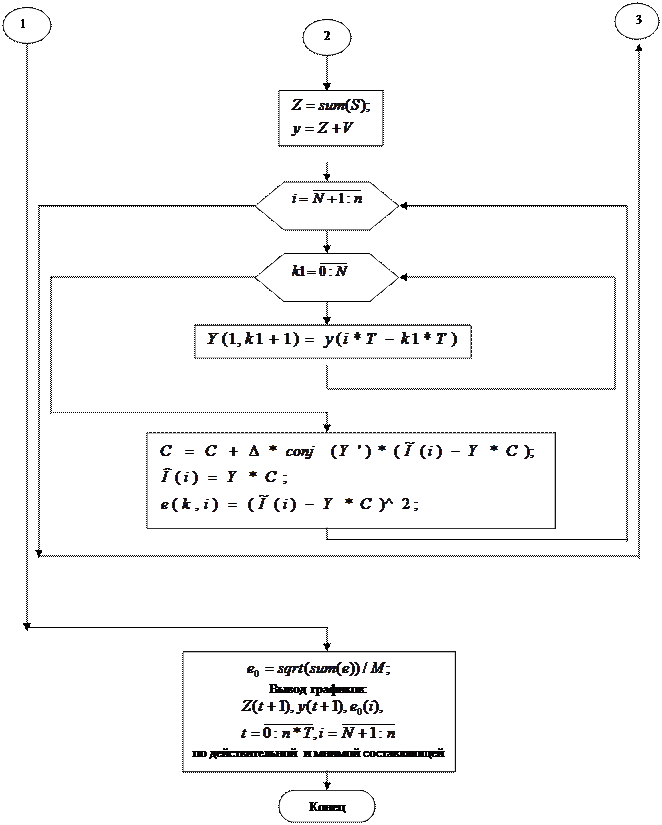
Операторы системы MATLAB, использованные в блок-схеме алгоритма, можно найти в [1].

Для моделирования алгоритма (6) на ЭВМ целесообразно использовать следующие данные: .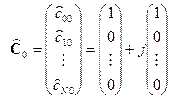

4. К заданию на лабораторную работу.

Для моделирования алгоритмов (5) и (6) на ЭВМ целесообразно использовать следующие данные: 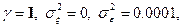начальные условия- ;

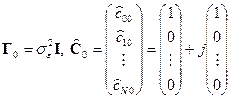ПРИЛОЖЕНИЕ

1. Модель канала связи с межсимвольной интерференцией (МСИ) и аддитивным белым гауссовским шумом (АБГШ).

Сигналы, передаваемые по каналу связи, сильно искажаются. Искажения чаще всего имеют вероятностный характер и могут быть аддитивными и (или) мультипликативными, так как присутствует шум и замирания. Кроме этого сигналы могут сдвигаться по частоте, испытывать нелинейные искажения. Так же происходит перекрытие принимаемых символов, которое называется межсимвольной интерференцией (МСИ). Причинами МСИ являются ограниченность и (или) неравномерность частотной характеристики канала, многолучевое распространение и т. д. Это препятствует повышению скорости передачи данных по каналам с ограниченной полосой. В данной лабораторной работе рассматривается линейный фильтровой канал с переменными параметрами. Искажения вносятся за счет МСИ и аддитивного белого шума.

Канал связи

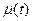
Рис. 1. Модель линейного фильтрового канала.

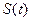
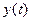, - сигнал на входе и выходе канала связи, 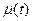-аддитивный гауссовский шум 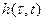- импульсная характеристик линейного канала связи.

.

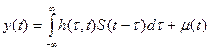Данная модель используется для описания физических каналов, у которых характеристики переменны во времени. Например, подводные акустические и ионосферные радиоканалы, каналы подвижной связи, которые возникают в условиях меняющегося во времени многолучевого распространения волн. При цифровой связи по коммутируемым телефонным сетям канал различен каждый раз при наборе нового номера, т.к. маршрут каждый раз различен. В этом случае можно представить 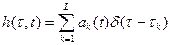, где 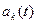- меняющиеся от времени коэффициенты затухания, 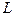- количество лучей (путей распространения), 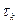- задержка 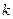-го луча. Тогда 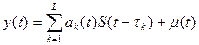. Или в дискретном времени 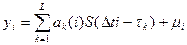. Здесь 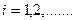- дискретное время, 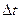- шаг дискретизации, определяемый по теореме Котельникова.

Далее более подробно рассмотрим однолучевой ограниченный по полосе канал с АБГШ. Его можно представить в виде трансверсального фильтра с коэффициентами 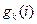, медленно меняющимися во времени. Предположим, что МСИ влияет на 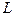символов. Эквивалентную модель такого канала можно записать следующим образом:

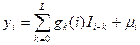, (1)

где 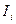-комплексная информационная последовательность символов, длительность одного символа равна , , 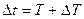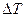- ошибка стробирования отсчетов, 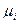- комплексная последовательность отсчетов белого гауссовского шума с нулевым средним, 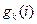учитывает импульсную характеристику фильтра передатчика, канала распространения и фильтра приемника. Моделью (1) можно описать некоторые виды сигналов цифровой модуляции, прошедшие через линейный фильтровой канал с АБГШ. Например, сигналы фазовой модуляции (ФМ) и квадратурной амплитудной модуляции (КАМ).

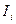
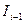
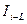
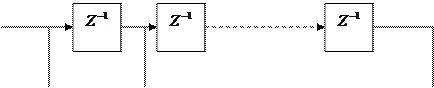
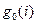
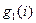
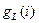
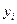
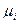
Рис. 2. Структурная схема канала с МСИ и АБГШ ( 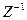- задержка на ).

Для таких каналов нет возможности синтезировать оптимальные фиксированные фильтры для демодулятора, т.к. характеристики каналов меняются во времени. Решение проблемы МСИ можно свести к синтезу приемника, который использует способ компенсации МСИ в принимаемом сигнале. Компенсатор МСИ называется эквалайзером или выравнивателем. Адаптивный эквалайзер проектируется так, чтобы приспосабливаться к меняющимся характеристикам канала.