Вывод нескольких графиков на одни оси

Для отображения нескольких графиков функций одной переменной на одних осях использовались возможности функций plot, plotyy, semilogx, semilogy, loglog. Они позволяют выводить графики нескольких функций, задавая соответствующие векторные аргументы парами, например plot(x,f,x,g). Однако для объединения трехмерных графиков их использовать нельзя. Для объединения таких графиков предназначена команда hold on, которую нужно задать перед построением графика. В следующем примере объединение двух графиков (плоскости и конуса) приводит к их пересечению. Конус задается параметрически следующими зависимостями:

, , , .

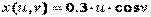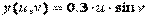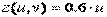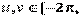
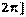Для графического отображения конуса сначала необходимо сгенерировать с помощью двоеточия вектор-столбец и вектор-строку, содержащие значения параметров на заданном интервале (важно, что u - вектор-столбец, а v-вектор-строка):

u = [-2*pi:0.1*pi:2*pi]';
v = [-2*pi:0.1*pi:2*pi];

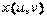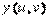Далее формируются матрицы X, Y, содержащие значения функций и в точках, соответствующих значениям параметров. Формирование матриц выполняется с помощью внешнего произведения векторов.

Замечание 2

Внешним произведением векторов 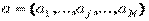, 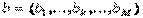называется матрица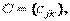 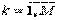размера N x M, элементы которой вычисляются по формуле .
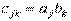Вектор а является вектор-столбцом ив MatLab представляется в виде двумерного массива размера N на один. Вектор-столбец bпри транспонировании переходит в вектор-строку размера один на М. Вектор-столбец и вектор-строка есть матрицы, у которых один из размеров равен единице. Фактически, С = abT, где умножение происходит по правилу матричного произведения. Для вычисления матричного произведения в MatLab используется оператор "звездочка". Определим внешнее произведение для двух векторов:

a = [1;2;3];
b = [5;6;7];
C = a*b'
C =
5 6 7
10 12 14
15 18 21

Сформируем матрицы X,Y, необходимые для графического отображения конуса:

X = 0.3*u*cos(v);
Y = 0.3*u*sin(v);

Матрица Z должна быть того же размера, что и матрицы X иY. Кроме того, она должна содержать значения, соответствующие значениям параметров. Если бы в функцию 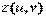входило произведение и и v, то матрицу Z можно было заполнить аналогично матрицам Xи Yпри помощи внешнего произведения. С другой стороны, функцию z(u,v)можно представить в ви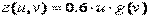де , где 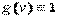. Поэтому для вычисления Zможно применить внешнее произведение векторов и 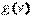, где вектор-строка имеет ту же размерность, что v, но состоит из единиц:

Z = 0.6*u*ones(size(v));

Все требуемые матрицы для отображения конуса созданы. Задание плоскости выполняется следующим образом:

[X,Y] = meshgrid(-2:0.1:2);
Z = 0.5*X+0.4*Y;

Теперь не сложно записать и полную последовательность команд для построения пересекающихся конуса и плоскости:

u = [-2*pi:0.1*pi:2*pi]';
v = [-2*pi:0.1*pi:2*pi];
X = 0.3*u*cos(v);
Y = 0.3*u*sin(v);
Z = 0.6*u*ones(size(v));
surf(X, Y, Z)
[X,Y] = meshgrid(-2:0.1:2);
Z = 0.5*X+0.4*Y;
hold on
mesh(X, Y, Z)
hidden off

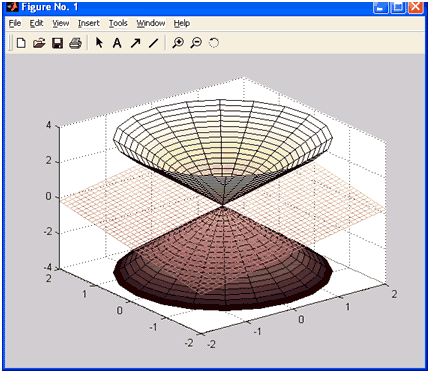
Команда hidden off применена для того, чтобы показать часть конуса, находящуюся под плоскостью.
Обратите внимание, что команда hold on распространяется на все последующие выводы графиков в текущее окно. Для размещения графиков в новых окнах следует выполнить команду hold off. Команда hold on может применяться и для расположения нескольких графиков функций одной переменной, например,

plot(x,f,х,g)

эквивалентно последовательности

plot(х,f)
hold on
plot(x,g)

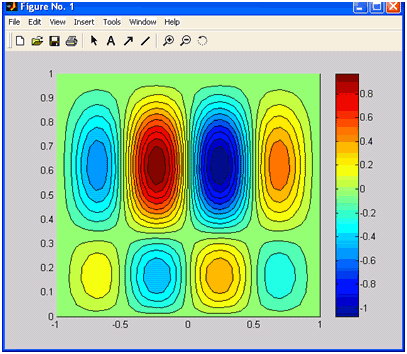
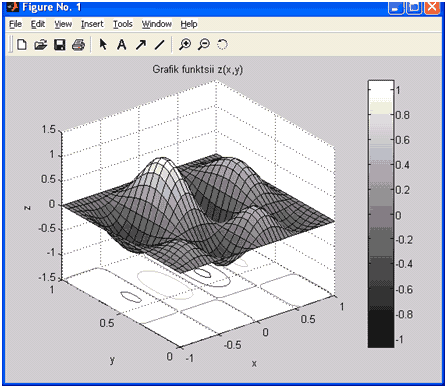
Результаты работы программы:

ПОСТРОЕНИЕ ТАБЛИЦ

Отображение функции в виде таблицы удобно, если имеется сравнительно небольшое число значений функции. Пусть требуется вывести в командное окно таблицу значений функции

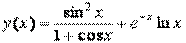
в точках 0.2, 0.3, 0.5, 0.8, 1.3, 1.7, 2.5.
Задача решается в два этапа.
1. Создается вектор-строка х, содержащая координаты заданных точек.
2. Вычисляются значения функции y(х)от каждого элемента вектора х и записываются полученные значения в вектор-строку у.
Значения функции необходимо найти для каждого из элементов вектор-строки х, поэтому операции в выражении для функции должны выполняться поэлементно.

» х = [0.2 0.3 0.5 0.8 1.3 1.7 2.5]
х =
0.2000 0.3000 0.5000 0.8000 1.3000 1.7000 2.5000 » у = sin(x).^2./(l+cos(x))+exp(-x).*log(x)
У =
-1.2978 -0.8473 -0.2980 0.2030 0.8040 1.2258 1.8764

Обратите внимание, что при попытке использования операций возведения в степень ^, деления / и умножения * (которые не относятся к поэлементным) выводится сообщение об ошибке уже при возведении sin(x) в квадрат:

» у = sin(х)^2/(1+соз(х))+exp(-x)*log(x)
??? Error using ==> ^
Matrix must be square.

Дело в том, что в MatLab операции * и ^ применяются для перемножения матриц соответствующих размеров и возведения квадратной матрицы в степень.
Таблице можно придать более удобный для чтения вид, расположив значения функции непосредственно под значениями аргумента:

» х
х =
0.2000 0.3000 0.5000 0.8000 1.3000 1.7000 2.5000 » у
у =
-1.2978 -0.8473 -0.2980 0.2030 0.8040 1.2258 1.8764

Часто требуется вывести значение функции в точках отрезка, отстоящих друг от друга на равное расстояние (шаг). Предположим, что необходимо вывести таблицу значений функции y(х)наотрезке [1, 2] с шагом 0.2. Можно, конечно, ввести вектор-строку значений аргумента х=[1, 1.2, 1.4, 1.6, 1.8, 2.0] из командной строки и вычислить все значения функции так, как описано выше. Однако, если шаг будет не 0.2, а, например 0.01, то предстоит большая работа по вводу вектора х.
В MatLab предусмотрено простое создание векторов, каждый элемент которых отличается от предшествующего на постоянную величину, т.е. на шаг. Для ввода таких векторов служит двоеточие (не путайте с индексацией при помощи двоеточия). Следующие два оператора приводят к формированию одинаковых вектор-строк. Условно можно записать

» х = [1, 1.2, 1.4, 1.6, 1.8, 2.0]
х =
1.0000 1.2000 1.4000 1.6000 1.8000 2.0000
» х = [1:0.2:2]
х =
1.0000 1.2000 1.4000 1.6000 1.8000 2.0000

Условно можно записать

х = [начальное значение : шаг : конечное значение]

Необязательно заботиться о том, чтобы сумма предпоследнего значения шага равнялась бы конечному значению, например, при выполнении следующего оператора присваивания

» х = [1:0.2:1.9]
х =
1.0000 1.2000 1.4000 1.6000 1.8000

Вектор-строка заполнится до элемента, не превосходящего определенное нами конечное значение. Шаг может быть и отрицательным:

» х = [1.9:-0.2:1]
х =
1.9000 1.7000 1.5000 1.3000 1.1000

В случае отрицательного шага для получения непустой вектор-строки начальное значение должно быть больше конечного.
Для заполнения вектор-столбца элементами, начинающимися с нуля и заканчивающимися 0.5 с шагом 0.1, следует заполнить вектор-строку, а затем использовать операцию транспонирования:

» х = [0:0.1:0.5]'
х =
0
0.1000
0.2000
0.3000
0.4000
0.5000

Обратите внимание, что элементы вектора, заполняемого при помощи двоеточия, могут быть только вещественными, поэтому для транспонирования можно использовать апостроф вместо точки с апострофом.
Шаг, равный единице, допускается не указывать при автоматическом заполнении:

» х = [1:5]
х =
1 2 3 4 5

Пусть требуется вывести таблицу значений функции

на отрезке [0, 1] с шагом 0.05,
Для выполнения этого задания необходимо произвести следующие действия:
1. Сформировать вектор-строку х при помощи двоеточия.
2. Вычислить значения у(х)отэлементов х.
3. Записать результат в вектор-строку y.
4. Вывести хи у.

» х = [0:0.05:1];
» у = ехр(-х).*sin(10*x);
» х
х =
Columns 1 through 7
О 0.0500 0.1000 0.1500 0.2000 0.2500 0.3000
Columns 8 through 14
0.3500 0.4000 0.4500 0.5000 0.5500 0.6000 0.6500
Columns 15 through 21
0.7000 0.7500 0.8000 0.8500 0.9000 0.9500 1.0000
» у
У =
Columns 1 through 7
0 0.4560 0.7614 0.8586 0.7445 0.4661 0.1045
Columns 8 through 14
-0.2472 -0.5073 -0.6233 -0.5816 -0.4071 -0.1533 0.1123
Columns 15 through 21
0.3262 0.4431 0.4445 0.3413 0.1676 -0.0291 -0.2001

Вектор-строки x и yсостоят из двадцати одного элемента, и не помещается на экране в одну строку, поэтому выводятся по частям. Так как х иy хранятся в двумерных массивах размерностью один на двадцать один, то выводятся по столбцам, каждый из которых состоит из одного элемента. Сначала выводятся столбцы с первого по седьмой (columns 1 through 7), затем - с восьмого по четырнадцатый (columns 8 through 14), и, наконец, - с пятнадцатого по двадцать первый (columns 15 through 21). Более наглядным и удобным является графическое представление функции.

[1]Источник: http://life-prog.ru/view_cat.php?cat=5