Прогнозирование экономических процессов с применением эконометрических моделей

Эконометрика — прикладная экономическая дисциплина, изучающая конкретные количественные взаимосвязи экономических объектов и процессов с помощью математико-статистических методов и моделей. Главным инструментом эконометрического исследования является модель. Выделяют три основных класса эконометрических моделей:

1) модель временных рядов;

2) модели регрессии;

3) системы одновременных уравнений.

Наиболее простым и часто используемым видом эконометрических моделей выступает регрессионная модель. Методическое обеспечение регрессионной модели предполагает выявление набора потенциально возможных факторов, оказывающих влияние на динамику исследуемого показателя. Далее, в рамках информационного обеспечения, формируются ряды наблюдений, что предполагает сбор статистических данных по выделенному кругу показателей либо в пространстве, либо во времени. На этом этапе важным является обеспечение методологической сопоставимости данных в пределах ряда. Далее переходят непосредственно к моделированию, пробуя различные виды зависимостей, и на основании статистических характеристик полученных моделей выбирают наилучшую.

Множественная регрессия явл. обобщением парной регрессии и исп-ся для описания зависимости между зависимой переменой У и независимыми переменными Х₁,Х₂,…,Х_k. Множественная регрессия м. б. лин. и нелин., но распространение в эк-ке получила линейная множественная регрессия.

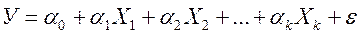
Выбор. регрессия: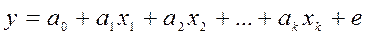

В качестве примеров моделей регрессии можно привести следующие модели:

а) производственная функция вида Q=f(L,K), выражающая зависимость объёма производства определённого товара (Q) от производственных факторов – от затрат капитала (К) и затрат труда (L);

б) функция цены Р=f(Q,Pk), характеризующая зависимость цены определённого товара (Р) от объема поставки (Q) и от цен конкурирующих товаров (Pk);

в) функция спроса Qd=f(P,Pk,I), характеризующая зависимость величины спроса на определённый товар (Р) от цены данного товара (Р), от цен товаров-конкурентов (Pk) и от реальных доходов потребителей (I).

Система одновременных уравнений— это система эконометрических уравнений, содержащая взаимозависимые переменные, которые включены в одно из уравнений модели в качестве результативного признака, а в другие уравнения - в качестве факторного признака. Пример: Кейнсианская модель потребления:

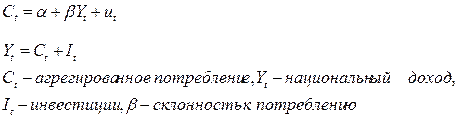
Модель описывает закрытую экономику без государственного вмешательства.

Из модели можно найти значение Y_t для любого момента времени.

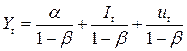
Примером системы одновременных уравнений является модель спроса и предложения, в которую входит три уравнения:

а) уравнение предложения: =а0+а1*Рt+a2*Pt-1;

б) уравнение спроса: =b0+b1* Рt+b2*It;

в) тождество равновесия: QSt = Qdt,

где QSt – предложение товара в момент времени t;

Qdt – спрос на товар в момент времени t;

Рt – цена товара в момент времени t;

Pt-1 – цена товара в предшествующий момент времени (t-1);

It– доход потребителей в момент времени.

В модели спроса и предложения выражаются две результативные переменные:

а) Qt– объём спроса, равный объёму предложения в момент времени t;

б) Pt– цена товара в момент времени t.

Моделью временных рядов называется зависимость результативной переменной от переменной времени или переменных, относящихся к другим моментам времени.

К моделям временных рядов, характеризующих зависимость результативной переменной от времени, относятся:

а) модель зависимости результативной переменной от трендовой компоненты или модель тренда;

б) модель зависимости результативной переменной от сезонной компоненты или модель сезонности;

в) модель зависимости результативной переменной от трендовой и сезонной компонент или модель тренда и сезонности.

Если временной ряд представлен суммой компонент – аддитивная модель (Yt=Tt+St+et); если в виде произведения компонент – мультипликативная модель (Yt=Tt*St*et); модель смешанного типа (Yt=Tt*St+et)

К моделям временных рядов, характеризующих зависимость результативной переменной от переменных, датированных другими моментами времени, относятся:

а) модели с распределённым лагом, объясняющие вариацию результативной переменной в зависимости от предыдущих значений факторных переменных;

б) модели авторегрессии, объясняющие вариацию результативной переменной в зависимости от предыдущих значений результативных переменных;

в) модели ожидания, объясняющие вариацию результативной переменной в зависимости от будущих значений факторных или результативных переменных.

Авторегрессионная модель р-го порядка (AR-модель) имеет вид:

y_t = β₀+β₁y_t-1 + β₂y_t-2 + … + β_py_t-p + ε_t (t = 1, 2, …,n) , где β₀, β₁,…, β_р – некоторые константы.

Она описывает изучаемый процесс в момент t в зависимости от его значений в предыдущие моменты t-1, t-2, …, t-p. Если исследуемый процесс y_t в момент t определяется его значениями только в предшествующий период, то рассматривают авторегрессионную модель1-го порядка (AR(1)) или марковский случайный процесс :

y_t = β₀+β₁y_t-1 + ε_t (t = 1, 2, …,n) . (3)

Наряду с авторегрессионными временных рядов в эконометрике рассматриваются также модели скользящей средней (не следует путать с аналогичным термином, используемым в технике сглаживания временных рядов), в которой моделируемая величина задается линейной функцией от возмущений (ошибок) в предыдущие моменты времени. Модель скользящей средней q-го порядка (МА-модель) имеет вид:

y_t = ε_t + γ₁ ε_t-1 + γ₂ ε_t-2 + … + γ_q ε_t-q .

В эконометрике используются также комбинированные модели временных рядов. Авторегрессионная модель скользящей средней (ARMA) имеет вид:

y_t = β₀+β₁y_t-1 + β₂y_t-2 + … + β_py_t-p + ε_t + γ₁ ε_t-1 + γ₂ ε_t-2 + … + γ_q ε_t-q .