Линейный однонаправленный список (L1-список )

L1-список отличается от L2 – списка тем , что он обеспечивает последовательный просмотр элементов только от начала к концу списка. Передвинуть указатель назад нельзя. Кроме того, в L1 – списке работать можно только за указателем, т.е впереди по ходу движения.

Набор методов для работы с L1 – списком:

1.Конструктор - создает по умолчанию пустой список.

2.Деструктор – уничтожает список.

3.Пуст ? (IsEmpty) - функция, проверяющая пустоту списка.

4.В начало – переход в начало списка.

5.Доступ для чтения 1-го элемента за указателем (GetAfter). (д)

6.Доступ для изменения 1-го элемента за указателем. (д)

7.Вперед - перемещение текущего указателя вправо .

8.В конце – функция, проверяющая положение текущего указателя списка.

_____________________

9.Вставить – вставка элемента после указателя.

10.Изъять - изъятие элемента после указателем.

11.Удалить – удаление в соответствующей части. (д)

12.Сделать пустым. (д)(массовая).

Методы 1-8 совпадают с методами последовательности, методы 9-12 – собственные методы L1 – списка.

Идея реализации.

1.

На основе сплошной памяти (массив фиксированной длины).

2. На основе двух стеков.

3. На основе односвязного списка без буфера.

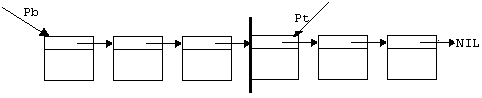В этом способе требуется указатель на последний элемент части «до» а также указатель на начало списка.

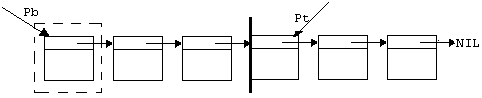
4. На основе односвязного списка с буфером.

Замечание. Для правильного анализа описанных выше абстрактных структур необходимо нарисовать все возможные варианты состояния структуры.

Динамический вектор.

Динамический вектор подобен простому вектору. Доступ к элементам вектора остается прямым и осуществляется с помощью индекса. Тип индекса может быть произвольным дискретным типом. Чаще всего индексы выбираются целочисленные.

Напишем набор методов для динамического вектора с целочисленными индексами и подвижной верхней границей. Считаем, что нижняя граница равна 1 и не может быть изменена.

1. Конструктор { cоздает пустой вектор}.

2. Деструктор {уничтожает вектор}.

3. Сделать пустым.

4. Пуст?

5. Верхний индекс º число элементов.

6. Добавить в конец.

7. Удалить из конца (или изъять из конца).

8. Доступ для чтения.

9. Доступ для записи.

Принципы реализации.

Заметим что, реализация динамического вектора может быть достаточно эффективной только на основе массива.

1). Реализация на основе одномерного массива.

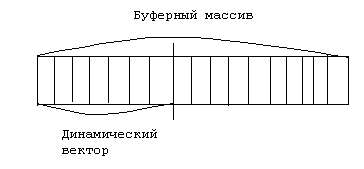
В этом случае выделяется буферный массив в части которого и располагается динамический вектор. При этом хранится индекс ячейки в которой расположен последний элемент вектора. Может возникнуть ситуация когда весь буферный массив будет заполнен. В этом случае придется выделять новый буфер, который больше предыдущего.

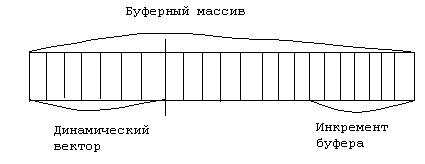
Затем необходимо перекопировать элементы из старого буфера в новый и дописать элемент. Величина на которую увеличивается буфер называется инкрементом буфера. При этом если в буфере освобождается слишком много места то можно провести обратную операцию. После каждой такой операции старый буфер необходимо уничтожить.

В случае использования такой модели можно добавить несколько операций:

А) Дополнительный конструктор (в качестве параметров задается начальная длина буфера и длина инкремента).

Б) Изменение длины инкрементной части.

В) Установить длину буфера (необходимо чтобы избежать массовых операций).

Данная модель реализации крайне неудобна. Она требует большое количество памяти, а также приводит к появлению массовых операций (например, копирование элементов буфера).

2). Модель реализации динамического вектора на основе двумерной таблицы.

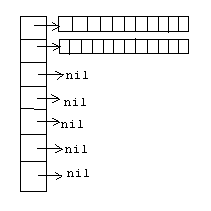
В этом случае создается массив указателей, который указывает на строки, в которых располагается динамический вектор. Если в текущей строке нет свободного места, то для добавления элемента выделяется память под новую строку и туда вписывается новый элемент. Удаление осуществляется в обратном порядке, но строка не удаляется. Удаление осуществляется в том случае если строк накопилось несколько.

Если двумерный массив заполнен полностью и необходимо добавить еще один элемент, то создается больший массив указателей. При этом копированию будут подвергаться уже указатель, что позволяет избежать массовости данной операции.

Возникает вопрос, возможно ли использовать более сложные модели (трехмерный, четырех мерный массивы). Да это возможно, но острой необходимости в этом нет. Практически во всех типах программ, где необходимо использование динамического вектора, достаточно одного из двух перечисленных выше типов для обеспечения быстроты работы программы.

Множество

Множество отличается от всех других структур данных прежде всего тем, что все операции происходят в теоретико-множественном смысле. Если добавляется существующий в множестве элемент, то изменения множества не происходит, а при удалении не находящегося в множестве элемента не возникает ошибочной ситуации. Рассмотрим подпрограммы необходимые для работы с множествами.

1. Конструктор { Init; } - создание пустого множества

2. Деструктор { Done; } - уничтожение множества

3. Сдеать пустым { DoEmpty; }

4. Пусто? { IsEmpty:boolean; }

5. Добавить { Insert(x:KeyType); } - добавить элемент в множество. Можно сделать функцию,

которая возвращает в качестве результата произошло ли реальное добавление элемента в

множество.

6. Удалить { Del(x:KeyType); } - удалить элемент из множества

7. Принадлежит? { IsPresent(x:KeyType):boolean; } - проверить, принадлежит ли данный

элемент множеству.

8. Взять какой-нибудь { Extract(var x:KeyType); } - взять произвольный элемент из

множества. Следует учитывать, что данная операция должна выполняться достаточно

быстро.

Общее требование ко всем реализациям - операции должны выполняться как можно быстрее. Существует очень много идей реализации множеств. Рассмотрим только некоторые:

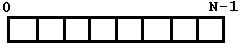
1) самая простая - битовая. Используется в том случае когда мощность множества А конечно

и невелико (пример: мощность множества символов - 256, мощность множества целых чисел

из небольшого диапазона - невелико). В этом случае можно построить функцию

взаимооднозначную функцию h(x): A _ I (где I - множество целых чисел от 0 до M-1

(M - мощность)) Для хранения используют битовую строку.

Иногда множество может начинаться с середина байта, т.е. функция отображает в число не от 0. Основное действие, которое делает конструктор - зануляет байты. Запись осуществляется путем поиска соответствующего элементу байта, а затем и бита, и занесение в него с помощью логического "или" значения 1. Удаление происходит почти также, но соответственный бит надо занулить. Если M - очень мало, то можно незначительно ускорить работу с множеством выделяя под элемент не бит, а байт (правда, тогда на реализацию множества будет тратится в 8 раз больше памяти, но зато можно осуществлять прямой

доступ к элементам).

2) реализация на базе массива

Есть несколько возможных видов реализации множеств на базе массивов. Рассмотрим только

некоторые. При данных типах реализации не требуется конечности множества A, но число

участвующих в операциях элементов должно быть конечно.

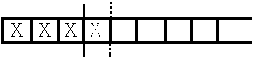а)

При добавлении необходимо пробежать по всей первой части в поисках добавляемого

элемента. Если он не найден, то добавляем элемент в конец и смещаем индекс

последнего элемента на 1. При удалении элемента мы опять пробегаем все элементы

массива до элемента на который указывает индекс конца массива. Если элемент не

обнаружен, то ничего не делаем, иначе удаляем его, смещая все элементы, стоящие за

ним, вправо. Все операции(за исключением команды "взять какой-нибудь") выполняются

за время пропорциональное числу элементов, поэтому данная форма организации

используется крайне редко и только для маленьких массивов. Подобную организацию

также возможно сделать на базе динамического вектора и списка.

б) на базе отсортированного массива. При такой организации облегчается поиск

элементов. Поиск элементов в отсортированном массиве можно осуществить за

логарифмическое время (например, с помощью метода деления пополам). Но изъятие и

добавление зависят от количества элементов. Такой тип организации используют в тех

программах, в которых сначала добавляется очень много элементов, после этого

множество не изменяется, а идет только проверка на принадлежность множеству.

Основные характеристики:

сортировка (нетривиальная) - за время ~n*log₂n

проверка на принадлежность - за время ~ log₂n

3) на основе хэш-функции

Есть несколько возможных видов реализации множеств с хэш-функциями. Рассмотрим только

два.

a) на базе массива элементов множества

Хэш-функция - это функция h(x):A _ I = 0..N-1, где N>=P (P - максимальное число

элементов которое может включать множество). Насколько большое число N надо взять –

это можно выяснить только путем обстоятельного исследования. В основном берут число

N раза в 2 или 3 превышающее P. При инициализации множества в него заносятся

какие-нибудь значения, которые заведомо не принадлежат множеству (например, если вы

намериваетесь хранить в множестве действительный числа из отрезка [0,1], то в

качестве заполняющего элемента можно взять число 2.0), при этом элементы равные

данному значению считаются пустыми. При добавлении элемента вычисляется значение

хэш-функции и делается попытка обратится к массиву с индексом равным значению

хэш-функции. Если данный элемент пустой, то добавляемый элемент записывается в это

место. Если же клетка оказалась и содержит значение не равное добавляемому

элементу, то идем вправо и записываем число в первую свободную ячейку. Благодаря

использованию хэш-функции добавление элементов осуществляется гораздо быстрее, но

количество пустых промежутков должно быть как можно быстрее, поэтому и число N

выбирается достаточно большим. Удаление осуществляется почти также, но реализовать

его довольно сложно, т.к. необходимо сдвинуть элементы на соответствующие значения

хэш-функции.

При таком способе заполнения массива элементы имеют тенденцию заполняться

неравномерно, поэтому часто заполняют массив с помощью квадратичной функции, т.е.

если элемент оказался не пустым, то обратиться ко второму после него, затем к 4, 16

и т.д. При этом надо так подобрать число N, чтобы функция пробегала все ячейки

массива. Кроме этого можно ввести дополнительную хэш-функцию.

б) может возникнуть вопрос - а почему бы не хранить в массиве указатели на структуры

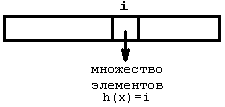хранящие элементы с заданным значение хэш-функции.

Тогда добавление и удаление можно реализовать проще. На подобных доводах и была

основана следующая реализация - хранение массива указателей на другие структуры. При

использовании данной организации уже не обязательно, чтобы N>=P. Но хэш-функция

должна быть выбрана так, чтобы слабо зависеть от элементов. Например, при хранении

рациональных дробей хэш-функция может быть функцией, берущей остаток от деления

знаменателя на какое-нибудь число. В результате время работы алгоритма достаточно

малое.

4) бинарное дерево

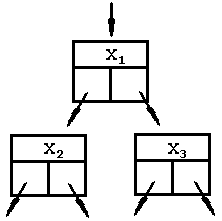Структура бинарного дерева изображена на рисунке, при этом дерево формируется так, чтобы для любого его узла X₂<X₁<X₃. Двоичное дерево называется идеально уравновешенным если для любого его узла справедливо, что в любом левом и правом поддереве количество элементов различается не более, чем на 1. Поиск в бинарном дереве выполняется за логарифмическое время зависящее от числа элементов множества <= глубине дерева и приблизительно равное log₂n. Вставка и удаление выполняется крайне сложно, т.к. надо уравновешивать дерево. Если же используется не сбалансированное дерево, то добавление упорядоченного множества элементов (будет нарастать только одна ветка) приведет к тому , что поиск будет выполняться за время n. Но если элементы поступают случайно, то такого не произойдет. Была доказана следующая теорема:

Теорема: Если элементы, вставляемые в множество, имеют равномерное распределение, то среднее время поиска больше времени поиска в идеально сбалансированном дереве не более, чем на 39 процентов (оценка статистическая).

Определение(Адельсона-Вельского и Ландиса): Дерево называется сбалансированным, если

для любого узла глубина левого поддерева отличается от глубины правого не более, чем

на 1.

Теорема: Глубина сбалансированного дерева может быть больше глубины идеально

сбалансированного дерева не более, чем на 45 процентов (оценка в самом худшем случае).

Время поиска в сбалансированных деревьях логарифмично, так что это достаточно хорошая

структура для хранения множеств. Кроме этого балансировка такого дерева осуществляется

всего за 3-4 операции, что не приводит к заметным увеличениям времени при добавлении и

удалении элементов.

Кроме бинарных деревьев существуют "страничные" деревья (B-деревья). Подробнее о них

можно узнать из книги Вирта "Алгоритмы + структуры данных = программы".

Нагруженное множество

Структура нагруженного множества отличается от структуры обычного множества ключей тем, что с каждым ключом связывается некоторое дополнительное значение. Например, если мы рассмотрим картотеку сотрудников некоторой организации, то ключом в этом случае будут табельные номера, а нагрузкой – информация о конкретном человеке.

Условимся обозначать тип нагрузки именем InfoType, а тип ключа – KeyType.

Рассмотрим методы, применимые к нагруженному множеству:

1. Конструктор (constructor Init;) – по умолчанию создает пустое множество.

2. Деструктор (destructor Done;) – уничтожает нагруженное множество.

3. Сделать пустым (procedure DoEmpty;).

4. Пусто (function IsEmpty : boolean;) – функция, возвращающая true если множество пусто, и false – если множество содержит элементы.

5. Добавить (procedure Insert( key : KeyType; info : InfoType);)- добавляет элемент с ключом key и нагрузкой info.

6. Удалить (procedure Delete(key : KeyType );) – удаляет элемент с ключом key.

7. Принадлежит (function IsPresent (key : KeyType) : boolean;) – проверяет принадлежность элемента множеству.

8. Взять (procedure Extract(var key : KeyType; var info : InfoType);)

9. Доступ для чтения (procedure Get(key : KeyType; var info : Infotype);)- читает элемент с ключом key.

10. Доступ для записи (procedure Put(key : KeyType; info : InfoType);)- изменяет элемент с ключом key.

Замечания к методам:

· Если при дополнении элемента этот элемент уже присутствует, тогда изменяется его нагрузка.

· При удалении элемента в случае необходимости можно передавать выходным параметром нагрузку элемента.

· Если при чтении требуемый элемент отсутствует, тогда одним из способов обработки исключительной ситуации является возвращение кода выполнения операции.

При сравнении методов обычного и нагруженного множества можно заметить, что методы нагруженного множества – это видоизмененные методы обычного плюс методы для чтения и записи.

Идеи реализации.

Принципы реализации нагруженного множества те же самые, что и у обычного, только теперь уже хранится как ключ, так и нагрузка.

Замечания к реализации:

· При реализации на основе битовой строки ключу сопоставляется номер в массиве указателей на нагрузку. Если элемент не принадлежит множеству, тогда соответствующий ключу указатель указывает на nil.

· С аналогичными поправками реализуются остальные принципы.

Итераторы.

Определение:

Абстракция итерации:

Для любого элемента х принадлежащего Абстрактной Структуре Данных (АСД)

выполнять

|

|

| действие (х)

|

|

конец итерации.

То есть для каждого элемента АСД должны выполняться некоторые действия, если действия должны выполняться только для элементов, обладающих некоторым свойством, тогда в цикл вставляется проверка на выполнение этого свойства для элементов АСД.

Протокол абстракции итерации обычно подразумевает, что при выполнении итератора АСД не разрушается, то есть, не меняет своего текущего состояния, действие итерации не приводит к изменению АСД, хотя в некоторых случаях допускается отклонение от этого протокола.

Рассмотрим АСД – таблицу:

Итератор: по всем значениям индексов произвести некоторое действие с элементом (например, чтение этого элемента), отвечающим конкретной паре индексов.

В случае стека итератору для доступа к элементам придется разрушить стек, во избежание разрушения необходимо скопировать структуру, то есть, неизбежны массовые операции. Для структур, в которых время доступа не ограничено константно, такие итераторы неэффективны.

Для повышения эффективности итераторов используют следующие приемы:

· Включить в протокол АСД дополнительные методы итератора

А) стартовать итератор.

Б) прочитать элемент (с продвижением).

В) проверить закончились ли элементы.

В этом случае можно создать цикл по структуре.

· Создать дружественный класс итератора

В этом случае итератор имеет прямой доступ к реализации структуры.

Недостатком 1-го способа является то, что к исходной структуре добавляются новые методы, недостатком 2-го способа является то, что для каждой АСД добавляется дружественный класс. Наиболее эффективным вариантом является создание класса перечисления для заданных способов реализации. То есть создается один единственный класс для определенного метода реализации различных структур. Этот способ считается более универсальным, так как мы работаем не с конкретной АСД а с ее реализацией, то есть таким подходом мы охватываем весь класс структур базирующихся на описанной реализации.

Замечания:

· Необходимо включить в АСД метод инициализации класса итератора.

· Необходимо переработать структуру файлов, так как для класса итератора могут быть необходимыми некоторые поля АСД.

Рассмотрим пример фрагментов итератора для односвязного списка:

{модуль итератора}

unit AEnum;

.

.

.

.

Type PEnumList1=^CEnumList1;

CEnumList1=object

Public

Constructor Init(Pstart,Pend : PLink);

Destructor Done; virtual;

Procedure ReadInfo (var x : Info);

Function IsNotEnd : boolean;

Private

Pt:PLink;

Pe:PLink;

.

.

.

{другие поля}

end;

Implementation

.

.

.

Constructor CEnumList1.Init;

Begin

Pt:=Pstart;

Pe:=Pend;

End;

Procedure CEnumList1.ReadInfo;

Begin

{. . .} – проверка существования следующего

x:=Pt^.Info;

Pt:=Pt^.Next;

End;

Function CEnumList1.IsNotEnd;

Begin

IsNotEnd:=(Pt=Pe);

End;

{модуль АСД (очередь)}

.

.

.

public

procedure StartEnum (var PEnum : pointer);

.

.

.

Implementation

Uses Aenum;

.

.

.

Procedure Queue.StartEnum;

Begin

New(PEnumList1(PEnum),Init(pb,nil);

End;

Использование итератора

.

.

.

Q.StartEnum(PIter);

While Piter^.IsNotEnd do

Begin

Piter^.ReadInfo(x);

{обработка значений х}

End;

Dispose(Piter,Done);

.

.

.

В классе AEnum можно также реализовать итераторы и для других реализаций.