Построение и уравнивание маршрутной и блочной фототриангуляции по методу независимых моделей

В этом методе построение и уравнивание сетей маршрутной и блочной фототриангуляции производят в два этапа.

Сначала по всем смежным (соседним) снимкам в каждом маршруте строятся фотограмметрические модели, а затем определяют элементы внешнего ориентирования каждой модели и координаты точек сети в системе координат объекта.

Определение элементов внешнего ориентирования фотограмметрических моделей в системе координат объекта производят следующим образом.

Для каждой связующей точки (находящейся в зоне тройного перекрытия снимков или в межмаршрутном перекрытии) измеренной в двух моделях и центра проекции общего для двух смежных моделей снимка составляют уравнения:

в которых координаты точки в і и ј моделях в системе координат объекта определяют по формулам :

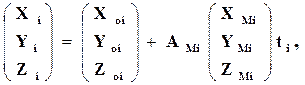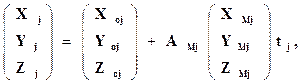а Xм_i,Yм_i, Zм_i и Xм_j, Yм_j, Zм_j – координаты точки в системах координат i и j моделях.

Для каждой опорной точки, измеренной на модели, составляются уравнения:

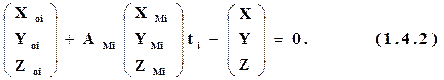Если при аэрофотосъемке с помощью системы GPS определялись координаты центров проекций снимков Xsk,Ysk,Zsk в системе координат объекта, то для каждого центра проекции составляются уравнения:

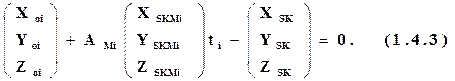В уравнениях Xskмi,Yskмi,Zskмi – координаты центра проекции k-го снимка в системе координат i-ой модели.

Уравнения поправок соответствующие уравнениям (1.4.1) имеют вид аналогичный уравнениям поправок (1.3.3), а уравнения поправок соответствующие уравнениям (1.4.2) и (1.4.3) имеют вид аналогичный уравнениям поправок (1.3.4) (см. раздел 1.3).

В результате решения полученной системы уравнений поправок по методу наименьших квадратов находят уравненные значения элементов внешнего ориентирования всех моделей в системе координат объекта.

Необходимо отметить, что если при аэрофотосъемке были определены с помощью системы GPS координаты центров проекций снимков, то можно построить и уравнять блочную сеть без использования опорных точек на земной поверхности. При построении и уравнивании маршрутной сети необходима, по крайней мере, одна опорная точка.

Это связано с тем, что центры проекции, являющиеся в данном случае опорными точками расположены практически на одной прямой.

По определенным значениям элементов внешнего ориентирования моделей определяют координаты точек сети центров проекции снимков в системе координат объекта:

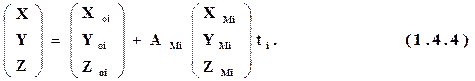Для точек сети и центров проекций снимков, координаты которых были определены по нескольким моделям, в качестве окончательного значения берутся средние значения этих координат.

Значения угловых элементов внешнего ориентирования снимков 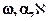определяют в два этапа.

Сначала находят матрицу преобразования координат снимка по формуле:

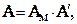(1.4.5)

В формуле1.4.5:

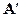- матрица преобразования координат, определяющая угловую ориентацию системы координат снимка Sxyz относительно системы координат модели O_MY_MX_MZ_M, элементы 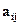которой являются функцией угловых элементов взаимного ориентирования 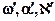i- го снимка.

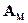- матрица преобразования координат, определяющая угловую ориентацию системы координат модели O_MY_MX_MZ_M относительно системы координат объекта OYXZ, элементы 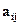которой являются функцией угловых элементов внешнего ориентирования модели ;

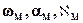По значениям элементов матрицы А вычисляют значения угловых элементов внешнего ориентирования снимка:

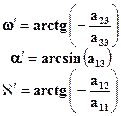
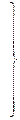. (1.4.6)

Угловые элементы внешнего ориентирования снимков ω, α, χ можно определить и из решения обратных засечек по координатам точек сети определенным в системе координат объекта и координатам их изображений измеренных на снимке.

При этом уравнения поправок для обратной засечки имеют вид:

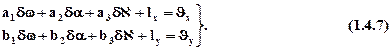Общее количество неизвестных, определяемых при построении и уравнивании сети можно определить по формуле:

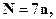
где n – количество независимых моделей.

Общее количество уравнений поправок можно определить по формуле:

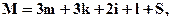
где m – количество связующих точек на смежных моделях;

k - количество планово-высотных опорных точек, измеренных на моделях;

i - количество плановых опорных точек, измеренных на моделях;

l – количество высотных опорных точек, измеренных на моделях;

S – количество уравнений поправок, составленных для центров проекций, определенных с помощью системы GPS.(S = 6n, где n – количество независимых моделей.)

Для сети изображенной на рис. 1.4.1 состоящей из двух маршрутов, в каждом из которых 4 снимка (3 стереопары):

,

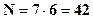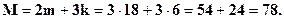
Если при этом координаты центров проекций были определены системой GPS, то дополнительно составляют j уравнений поправок:

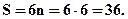
Таким образом, M=114

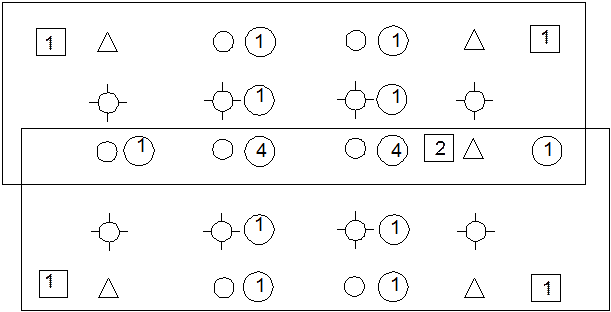
Рис. 1.4.1

- главная точка снимка;

- точка сети;

- планово-высотная точка;

m - количество связующих точек на смежных моделях;

- количество планово-высотных опознаков, измеренных на моделях.