Синтез комбинационных логических цепей
Комбинационная логическая цепь (КЛЦ) – это цепь, логическое состояние выходов которой зависит только от комбинации логических сигналов на входах в данный момент времени. КЛЦ реализуются обычно либо на элементах И-НЕ, либо ИЛИ-НЕ. Процесс синтеза КЛЦ выполняется в три этапа.
А) Составляют таблицу функционирования КЛЦ (таблицу истинности). Если функция задана в аналитической форме, то таблица истинности составляется так: аргументам задаются значения «0» и «1» и из выражения находят значение функции. При этом возможных сочетаний аргументов будет 2n, где n – число аргументов, т. е. входных сигналов.
Б) Заполняют диаграмму Вейча (карту Карно) и производят минимизацию. Записывают из диаграммы минимизированное выражение функции.
В) На заданном элементом базисе (И-НЕ или ИЛИ-НЕ) выполняем схему, соответствующую минимизированному выражению. Для этого выражение с помощью правил де-Моргана предварительно преобразуется в форму, удобную для реализации либо на ячейках И-НЕ (выражение должно содержать только логическое умножение), либо на ячейках ИЛИ-НЕ (выражение должно содержать только логическое сложение). После такого преобразования схема составляется непосредственно на основе логического выражения функции.
Пример. Составить КЛЦ для функции 
.
Минимизацию проводим с помощью карт Карно и получаем: F = ab + a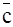 
. Пользуясь правилами де-Моргана, преобразуем это выражение для реализации на элементах И-НЕ:
.
Составляем на основе этого выражения схему (рисунок 2.7). Составление схемы начинаем от конца, т. е. с верхней (общей) инверсии. Конъюнкция под знаком этой инверсии даёт последнюю ячейку И-НЕ. Число её входов должно быть равно числу сомножителей под знаком инверсии. Если требуется просто инвертор, то он образуется из ячейки И-НЕ объединением всех её входов.
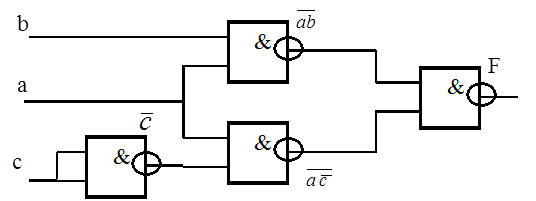
Рисунок 2.7 – Реализация функции ab + a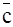
Часто используются КЛЦ, выполненные в виде интегральных схем различных серий, соответствующих схемотехническим базисам: транзисторно-транзисторной логики (ТТЛ), логики на комплементарных МОП-транзисторах (КМДП) (старое КМОП), эмиттерно-связанной логики (ЭСЛ) и буферизированной полевой логики (БПЛ). Функция, выполняемая ИС, даётся либо в виде условного обозначения и логического выражения, либо в виде словесной характеристики.
Интегральные схемы ТТЛ имеют базовый элемент на основе биполярных транзисторов и характеризуются следующими уровнями логических сигналов: напряжение низкого уровня uL = [0; 0,3] В; напряжение высокого уровня uh = [2,4; 5] В. Напряжение питания этих ИС равно 5 В. Из наиболее часто встречающихся в практике ИС этого типа можно отметить следующие серии: К133, 155, 533, 555, 530, 531, 1533, 1531. В основной массе задач целесообразно применять серию 1533.
ИС КМДП имеют базовый элемент в виде логического ключа на комплементарных (разных по природе, но идентичных по электрическим характеристикам) полевых транзисторах и характеризуются практическими уровнями логических сигналов, примерно равными: напряжение низкого уровня uL » 0; напряжение высокого уровня uh примерно равно напряжению питания. В зависимости от серии, напряжение питания этих ИС лежит в диапазоне от 1,5 В до 15 В. Из часто встречающихся в практике ИС этого типа можно указать следующие серии: К564, 561, 1564, 1561, 1554, 1594, 5554.
Основная особенность этих ИС – очень малая потребляемая мощность от источника питания (микроватты). Поэтому их целесообразно использовать в автономных устройствах.
В ЭСЛ ИС в базовом элементе применён токовый ключ – дифференциальный каскад на БПТ в ключевом режиме. Напряжение питания серии 1500 равно минус 4,5 В, а остальные серии питаются напряжением минус 5,2 В. Напряжение низкого уровня uL лежит в интервале [–1,8; –1,6] B; напряжение высокого уровня uh равно в среднем значению минус 0,8 В. Особенность ЭСЛ ИС – это наличие парафазного (прямого и инверсного) выхода, причём с открытым эмиттером. Поэтому используемый выход должен быть подключён к шине питания через резистор сопротивлением 300–500 Ом. Можно привести серии ЭСЛ ИС: К100, 500, 1500.
Основная особенность этих ИС – высокое быстродействие и большая потребляемая мощность. Например, ряд функциональных элементов серии 1500 работают на частотах до 500 МГц.
В БПЛ ИС в базовом элементе также применён токовый ключ – дифференциальный каскад на ПТ с барьером Шотки в ключевом режиме. Элементы с барьером Шотки имеют очень высокое быстродействие – время перехода из одного состояния в другое лежит в пикосекундном диапазоне. В качестве материала применяют арсенид галлия (GaAs). Питание этих ИС производится от двух источников: 4,5 В и минус 2,5 В. Напряжение низкого уровня uL лежит в интервале [–0,2; 0,1] B; напряжение высокого уровня uh в диапазоне [0,9; 1,5] В. БПЛ ИС также имеют парафазный выход, но с открытым истоком. Используемый выход должен быть подключён к общему проводу («земле») через резистор сопротивлением 25–150 Ом. Основная серия этих ИС – серия К6500.
Минимизация функции. Минимизация (упрощение формы записи) функции позволяет минимизировать схему и реализовать её с наименьшим числом элементов. Выявить и устранить избыточность в записи функции можно использованием аксиом, законов, тождеств и теорем алгебры логики. Для минимизации функции с числом переменных до пяти-шести наиболее удобным является метод карт Карно.
Пример. Рассмотрим процесс минимизации на примере четырех переменных х, у, z и v функции, заданной следующим логическим выражением:
.
Представим эту функцию в виде:
.
Эта функция выражается в совершенной дизъюнктивной нормальной форме (СДНФ):
.
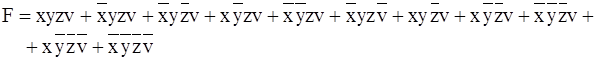Функция состоит из 11 минтермов, в связи с чем на карте Карно (рисунок 2.8) ее будут представлять 11 клеток, отмеченных единицами. Так, первый минтерм функции хуzv будет отображаться клеткой, имеющей координаты ху и zv, соответственно 11 и 11. Пять клеток карты остаются свободными.
Рисунок 2.8 – Карта Карно функции F(x, y, z, v)
Затем на карте Карно необходимо определить соседние минтермы (клетки) и объединить их в минимальное количество групп соседних минтермов (клеток). Для наглядности выделенные группы соседних клеток показывают сплошными линиями. Минимальное количество групп соседних минтермов для рассматриваемой функции будет равно трем. В первую группу входят две нижние клетки второго столбца слева с минтермами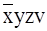 
и 
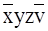. В соответствии с аксиомой (x + 
) = 1 имеем:
,
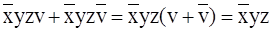т. е. переменная v из этой группы может быть исключена. Вторая группа состоит из двух пар верхних клеток крайних столбцов, определяющих минтермы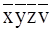 
, 
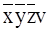и 
, 
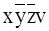. Сумма этих минтермов даёт:
,
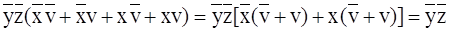т. е. из группы исключаются две переменные: х и v. Третья группа состоит из восьми клеток второй и третьей строк, для которых v = 1, а переменные х, у, z входят с прямыми и инверсными значениями, в связи с чем переменные х, у, z из этой группы могут быть исключены ( 
). Сумма минтермов обеих строк будет равна v. На основании проведенных операций получаем минимальную функцию, выраженную в ДНФ:
.
Карта Карно позволяет также провести минимизацию той же функции в КНФ по нулевым значениях минтермов, находящихся в пустых клетках карты (рисунок 2.8) и определяющих нулевое значение функции, т. е. ее инверсное значение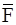 
. Порядок проведения минимизации сохраняется прежним. Минимизирующие контуры, охватывающие соседние клетки с нулевым значением минтермов рассматриваемой функции, показаны на рисунке пунктиром.
Минимизация функции в ДНФ или КНФ равноправна. Представление результата минимизации в ДНФ или КНФ зависит от вида функции и состава используемых логических элементов. Реализация функции в ДНФ требует преимущественного использования логических элементов И (И-НЕ), а в КНФ – логических элементов ИЛИ (ИЛИ-НЕ). При использовании логических элементов И (И-НЕ) логическую функцию целесообразно представить в виде произведения переменных, а логических элементов ИЛИ (ИЛИ-НЕ) – в виде суммы переменных.