Вычисления с массивами

В традиционных языках программирования вычисления с массивами осу­ществляются поэлементно в том смысле, что нужно запрограммировать каж­дую отдельную операцию над отдельным элементом массива. В М-языке сис­темы MATLAB допускаются мощные групповые операции над всем массивом сразу. Именно групповые операции системы MATLAB позволяют чрезвычайно компактно задавать выражения, при вычислении которых реально выполняется гигантский объем работы.

Операции сложения и вычитания матриц (знакомые вам из линейной ал­гебры) обозначаются стандартными знаками + и -.

Задайте матрицы А и В и выполните операцию сложения матриц: » A=[1 1 1; 2 2 2; 3 3 3]; B=[0 0 0; 7 7 7; 1 2 3]; » A+B

Если используются операнды разных размеров, выдается сообщение об ошибке, за исключением случая, когда один из операндов является скаляром. При выполнении операции А + скаляр (А – матрица) система расширит скаляр до массива размера А, который и складывается далее поэлементно с А.

» A+5

ans = 6 6 6

7 7 7

8 8 8

Для поэлементного перемножения и поэлементного деления массивов одинаковых размеров, а также поэлементного возведения в степень массивов, применяются операции, обозначаемые комбинациями двух символов: .*,./,и.^. Использование комбинаций символов объясняется тем, что символами * и / обозначены специальные операции линейной алгебры над векторами и матри­цами.

Кроме операции ./, называемой операцией правого поэлементного деления,

есть еще операция левого поэлементного деления .\. Объясним разницу между

этими операциями. Выражение А / В приводит к матрице с элементами А (k, m) /В (k, m), а выражение А . \ В приводит к матрице с элементами В (k, m) /А (k, m).

Знак * закреплен за перемножением матриц и векторов в смысле линейной алгебры.

Знак \ закреплен в системе MATLAB за решением довольно сложной зада­чи линейной алгебры - нахождением корней системы линейных уравнений. Например, если требуется решить систему линейных уравнений Ay = b, где А - заданная квадратная матрица размера N x N, b - заданный вектор-столбец длины N, то для нахождения неизвестного вектор-столбца у достаточно вычислить выражение А \ b (это равносильно операции: ).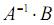

Типичные задачи аналитической геометрии в пространстве, связанные с нахождением длин векторов и углов между ними, с вычислением скалярного и векторного произведений, легко решаются разнообразными средствами систе­мы MATLAB. Например, для нахождения векторного произведения векторов предназначена специальная функция cross, например:

» u=[1 2 3]; v=[3 2 1]; » cross(u,v)

ans = -4 8 -4

Скалярное произведение векторов можно вычислить с помощью функции общего назначения sum, вычисляющей сумму всех элементов векторов (для матриц эта функция вычисляет суммы для всех столбцов). Скалярное произве­дение, как известно, равно сумме произведений соответствующих координат (элементов) векторов. Таким образом, выражение: » sum(u.*v)

вычисляет скалярное произведение двух векторов u и v. Скалярное произведе­ние можно также вычислить как: u*v′.

Длина вектора вычисляется с помощью скалярного произведения и функ­ции извлечения квадратного корня, например: » sqrt(sum(u.*u))

Ранее рассмотренные для скаляров операции отношения и логические опе­рации выполняются в случае массивов поэлементно. Оба операнда должны быть одинаковых размеров, при этом операция возвращает результат такого же размера. В случае, когда один из операндов скаляр, производится его предвари­тельное расширение, смысл которого уже был пояснен на примере арифметиче­ских операций.

Среди функций, генерирующих матрицы с заданными свойствами, упомя­нем здесь функцию eye, производящую единичные квадратные матрицы, а так­же широко применяемую на практике функцию rand, генерирующую массив со случайными элементами, равномерно распределенными на интервале от 0 до1. Например, выражение » F=rand(3)

порождает массив случайных чисел размером 3х3 с элементами, равномерно распределенными на интервале от 0 до 1.

Если вызвать эту функцию с двумя аргументами, например R=rand(2,3),то получится матрица R случайных элементов размером 2x3. При вызове функции rand с тремя и более скалярными аргументами производятся многомерные мас­сивы случайных чисел.

Определитель квадратной матрицы вычисляется с помощью функции det.

Среди функций, производящих простейшие вычисления над массивами, помимо рассмотренной выше функции sum, упомянем еще функцию prod, ко­торая во всем аналогична функции sum, только вычисляет она не сумму эле­ментов, а их произведение. Функции max и min ищут соответственно макси­мальный и минимальный элементы массивов. Для векторов они возвращают единственное числовое значение, а для матриц они порождают набор экстре­мальных элементов, вычисленных для каждого столбца. Функция sort сортиру­ет в возрастающем порядке элементы одномерных массивов, а для матриц она производит такую сортировку для каждого столбца отдельно.

Наконец, рассмотрим уникальную возможность М-языка системы MATLAB производить групповые вычисления над массивами, используя обыч­ные математические функции, которые в традиционных языках программиро­вания работают только со скалярными аргументами. В результате с помощью крайне компактных записей, удобных для ввода с клавиатуры в интерактивном режиме работы с командным окном системы MATLAB, удается произвести большой объем вычислений. Например, всего два коротких выражения

» x=0:0.01:pi/2; y=sin(x);

вычисляют значения функции sin сразу в 158 точках, формируя два вектора x и у со 158 элементами каждый.