Формирование моделей на макроуровне
Исходное математическое описание процессов в объектах на макроуровне представлено системами обыкновенных дифференциальных и алгебраических уравнений. Аналитические решения таких систем при типичных значениях их порядков в практических задачах получить не удается, поэтому в САПР преимущественно используются алгоритмические модели.
Исходными для формирования математических моделей объектов на макроуровне являются компонентные и топологические уравнения:
· Компонентными называют уравнения, описывающие свойства элементов (компонентов), другими словами, это уравнения математических моделей элементов (ММЭ).
· Топологические уравненияописывают взаимосвязи в составе моделируемой системы.
В совокупности компонентные и топологические уравнения конкретной физической системы представляют собой исходную математическую модель системы (ММС).
Компонентные и топологические уравнения в системах различной физической природы отражают разные физические свойства, но могут иметь одинаковый формальный вид. Одинаковая форма записи математических соотношений позволяет говорить о формальных аналогиях компонентных и топологических уравнений. Такие аналогии существуют для механических поступательных, механических вращательных, электрических, гидравлических (пневматических), тепловых объектов.Единство математического аппарата формирования ММС особенно удобно при анализе систем, состоящих из физически разнородных подсистем.
В общем виде компонентные и топологические уравнения имеют вид:
Fк (dV/dt, V, t) = 0, (4.1)
Fт (V) = 0, (4.2)
где V= (v1, v2, ...vn) — вектор фазовых переменных, t — время.
Различают фазовые переменные двух типов, их обобщенные наименования — фазовые переменные типа потенциала (например, электрическое напряжение) и типа потока (например, электрический ток). Каждое компонентное уравнение характеризует связи между разнотипными фазовыми переменными, относящимися к одному компоненту (например, закон Ома описывает связь между напряжением и током в резисторе), а топологическое уравнение — связи между однотипными фазовыми переменными в разных компонентах.
Модели можно представлять в виде систем уравнений или в графической форме, если между этими формами установлено взаимно однозначное соответствие. В качестве графической формы часто используют эквивалентные схемы.
Так в электрических системах фазовыми переменными являются электрические напряжения и токи. Компонентами систем могут быть простые двухполюсные элементы и более сложные двух- и многополюсные компоненты. К простым двухполюсникам относятся следующие элементы: сопротивление, емкость и индуктивность, характеризуемые одноименными параметрами: R, C, L. В эквивалентных схемах эти элементы обозначают в соответствии с рис. 4.1.
Компонентные уравненияпростых двухполюсников имеют вид:
для R: u = i R (закон Ома), (4.3)
для C: i = C du/dt, (4.4)
для L: u = L di/dt, (4.5)
где u— напряжение (точнее, падение напряжения на двухполюснике), i — ток.
Эти модели лежат в основе моделей других возможных более сложных компонентов. Большая сложность может определяться нелинейностью уравнений (4.3) — (4.5) (т.е. зависимостью R, C, L от фазовых переменных), или учетом зависимостей параметров R, C, L от температуры, или наличием более двух полюсов. Однако многополюсные компоненты могут быть сведены к совокупности взаимосвязанных простых элементов.
Топологические уравнениявыражают законы Кирхгофа для напряжений (ЗНК) и токов (ЗТК). Согласно ЗНК, сумма напряжений на компонентах вдоль любого замкнутого контура в эквивалентной схеме равна нулю, а в соответствии с ЗТК сумма токов в любом замкнутом сечении эквивалентной схемы равна нулю:
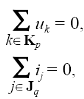
где Kp— множество номеров элементов р-го контура, Jq— множество номеров элементов, входящих в q-е сечение.

Рис. 4.1 Условные обозначения простых элементов в эквивалентных схемах:
а – электрических, б – механических.
Известен ряд методов формирования ММС на макроуровне. Получаемые с их помощью модели различаются ориентацией на те или иные численные методы решения и набором базисных переменных, т.е. фазовых переменных, остающихся в уравнениях итоговой ММС. Общим для всех методов является исходная совокупность топологических и компонентных уравнений.
При записи топологических уравнений удобно использовать промежуточную графическую форму — представление модели в виде эквивалентной схемы, состоящей из двухполюсных элементов. Общность подхода при этом сохраняется, так как любой многополюсный компонент можно заменить подсхемой из двухполюсников. В свою очередь эквивалентную схему можно рассматривать как направленный граф, дуги которого соответствуют ветвям схемы. Направления потоков в ветвях выбираются произвольно (если реальное направление при моделировании окажется противоположным, то это приведет лишь к отрицательным численным значениям потока). Выбор дерева однозначно определяет вектора напряжений Uх и токов Ix хорд, напряжений Uвд и токов Iвд ветвей дерева и приводит к записи топологических уравнений в виде:
Uх + MUвд = 0,
Iвд - MTIx = 0,
где М —матрица контуров и сечений, MT — транспонированная М-матрица.
В качестве примера рассмотрим электрическую схему:

Для получения топологических уравнений все ветви эквивалентной схемы разделяют на подмножества хорд и ветвей дерева. Имеется в виду покрывающее(фундаментальное) дерево, т.е. подмножество из β-1 дуг, не образующее ни одного замкнутого контура, где β— число вершин графа (узлов эквивалентной схемы). На рис. 4.2показан граф и эквивалентная схема, толстыми линиями выделено одно из возможных покрывающих деревьев.
В М-матрице число строк соответствует числу хорд, число столбцов равно числу ветвей дерева. М-матрица формируется следующим образом. Поочередно к дереву подключаются хорды. Если при подключении к дереву р-й хорды q-я ветвь входит в образовавшийся контур, то элемент Мpq матрицы равен +1 при совпадении направлений ветви и подключенной хорды, Мpq = -1 при несовпадении направлений. В противном случае Мpq = 0.
Для рассматриваемой схемы, М-матрица представлена в виде табл. 4.1.
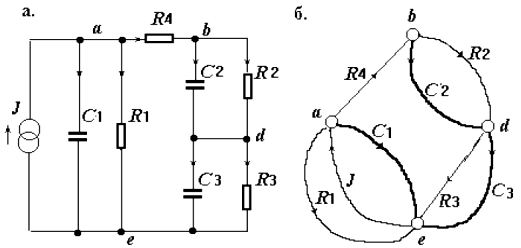
Рис. 4.2 Эквивалентная схема (а) и ее граф (б).
Таблица 4.1

