Дискретно-детерминированные модели

Дискретно-детерминированные модели используются для описания объектов, среди свойств которых доминирующее значение имеют два:

отсутствие случайностей (их либо нет в реальности, либо ими пренебрегают из-за их несущественности с позиции цели исследования);

явления в объектах моделирования рассматривают как изменяющиеся во времени процессы, которые представительно описываются временными рядами.

Шаг изменения времени принимается постоянным, равным единице, при этом сколько реального времени работы объекта подразумевается в одном шаге изменения времени в модели (секунда, 2 дня, месяц и т.п.), решает разработчик модели. Примерами подобных объектов моделирования могут служить производственно-складские системы, финансово-хозяйственные механизмы функционирования экономических систем и т.п.

Для построения дискретно-детерминированных моделей в качестве теоретических схем формализации обычно используют два математических аппарата: конечно-разностные уравнения и теорию конечных автоматов.

Пример построения и использования дискретно-детерминированных моделей.Этот пример показывает, как используется аппарат конечно-разностных уравнений для построения дискретно-детерминированной модели. Причем эта модель строится в виде математических уравнений, для которых возможно нахождение аналитического решения.

Пусть имеется следующая ситуация: есть некоторый товар, цена P_t на который формируется на основе спроса на него и предложения товара на рынке. Допустим, что спрос D, на товар обратно пропорционален цене:

D_t= K₁-k₁P₁

где K₁— коэффициент; k₁ — коэффициент пропорциональности. Предложение товара S_t (его производство, так как полагаем здесь, что все что произведено, сразу предлагается к продаже) также ориентировано на цену с запаздыванием на один временной шаг (т. е. ориентируется на «вчерашнюю» цену):

S_t = K₂ + k₂P_t-1

где K₂ — коэффициент; k₂ — коэффициент пропорциональности. Условие локального равновесия на рынке товара определяется равенством спроса и предложения:

D_t=S_t, т.е.

K₁-k₁P₁= K₂ + k₂P_t-1

или

k₁P₁+ k₂P_t-1= K₁ - K₂ (2)

Решим уравнение (2), для чего сначала найдем решение однородного уравнения:

k₁P_t + k₂P_t-1= 0;(3)

P_t =µ ^t

k₁µ^t+ k₂µ^t-1= 0;

µ^t-1(k₁µ+ k₂)=0, µ^t-1≠0

µ = - k₂ / k₁

Общее решение однородного уравнения (3):P _t = R(- k₂ / k₁) ^t

где R — произвольная константа.

Найдем частное решение уравнения (2). Правая его часть — константа

К₁-К₂, поэтому и частное решение мы будем искать в виде константы ŷ.

k₁ ŷ+ k₂ ŷ= K₁ - K₂

K₁ - K₂

ŷ= ---------------

k₁+ k₂

Общее решение уравнения (2):

P_t=R(-k₂ / k₁) ^t + K₁ - K₂

--------------- .

k₁+ k₂

Положив P_t =P₀, при t=0, найдем значение для R:

P₀ = R(- k₂ / k₁) ⁰ + K₁ - K₂

_{_______________________} _________

k₁+ k₂

Окончательная формула для общего решения уравнения (2):

K₁ - K₂

_{_____________________} P_t =_{__} P_{0 -} _________ (- k₂ / k₁) ^t K₁ - K_{2 (4)}

k₁+ k₂ k₁+ k₂

Это решение показывает динамику цены. Например, для случая К₁= 200, k₁= 0,4, К₂ = 100, k₂ = 0,3 график ее изменения показан на рис. 3.3. Частное решение P_t = 143 соответствует равновесному состоянию.

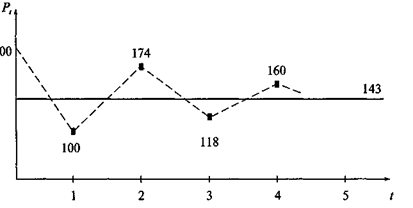
Рис. 3.3. Динамика цены

Свойства решения уравнения (4) определяются соотношением между коэффициентами k₂и k₁. При k₂ < k₁колебания цены вокруг равновесного значения имеют затухающую амплитуду (рис. 3.4) и значение цены сходится к значению равновесной цены; при k₂ = k₁колебания цены происходят с постоянной амплитудой (рис. 3.5), а при k₂ > k₁ — с увеличивающейся, т. е. мы имеем дело с расходящимися колебаниями (рис. 3.6).

Усложним условия только что рассмотренной ситуации. Пусть локальное равновесие рынка пытаются поддержать не только за счет производства, но и за счет запасов продукции Z_t.

Рис. 3.5. Колебания цены с постоянной амплитудой колебания цены

Рис.3.6.Расходящиеся колебания цены

Уравнения, описывающие ситуацию:

D_t=K₁-k₁P_t;

S_t=K₂+DP _t-1

ΔZ _t =Z _t –Z _t-1= S _t-D _t ;

P_t =P_t-1 – λΔZ_t-1,λ∩(0,1)(5)

Здесь цена ориентируется на уровень запасов товара в системе. Если этот уровень растет, то цена уменьшается, и наоборот. Коэффициент Я показывает долю величины изменения запасов, на которую будет скорректирована цена. Приведенные уравнения позволяют исключить все переменные и построить обобщенное уравнение для описания динамики цены:

P_t =P_t-1 – λΔZ_t-1 =P_t-1- λ(S _t-1-D _t-1)

P_t =P_t-1 – λ(К₂+DP _t-2 - K₁ + k₁P_t-1)

P_t–(1- λ k₁) P_t-1+ λDP _t-2= λ(K₁ - K₂)

(6)

Полученное уравнение (6) можно решить так, как это показано выше. Мы не будем этого делать. Обсудим характер данного уравнения. По своей сути — это модель описанной выше ситуации. Но и система уравнений (5) также есть модель. Разница между ними состоит в степени детализации описания ситуации. Модель (6) относится к типу «вход—выход», т.е. мы стремились все соотношения в модели свести к уравнению динамики вида (4), когда слева от знака равенства находятся значения переменной или переменных, описывающих выходные характеристики системы, а справа — входные.