Тема 2.1 Определение количества информации. Формула Хартли
Модуль 2. Измерение информации. Количество информации.
Основные понятия: количество информации, аддитивная мера Хартли.
Условные обозначения:
 - задания до чтения текста |  - задания во время чтения |  - задания после чтения |
| | Вспомните, как часто вам приходилось слышать: «Это невозможно измерить!», «Есть вещи, которые не могут быть подвержены количественной оценке!». Как вы считаете, эти люди правы? А можно ли измерить информацию? |
| | Прочитайте текст. Во время чтения делайте пометки на полях: «!» - важно, «?» - не понятно, есть вопросы | |||||
Чтобы измерить количество информации, содержащееся в сообщении или сигнале, можно воспользоваться так называемой аддитивной мерой Хартли. Введем понятия глубины сообщения и длины сообщения. Глубина сообщения q – количество различных элементов (символов, знаков), принятых для представления сообщений. В каждый момент времени реализуется только один какой-либо элемент. Длина сообщения n – количество позиций, необходимых и достаточных для представления сообщений заданной величины. При заданных глубине и длине сообщения количество всех возможных сообщений (N), которое можно представить: N = q n. Задача 1. Подсчитать количество всех трехбуквенных русских слов. Решение Всего трехбуквенных русских слов N = 323 = 32768. Заметим, что в это количество включены и «совершенно невозможные» слова, например «ааа» или «ььы», но, подчеркнем, что при описываемом подходе смысл (семантика) сообщения не рассматривается. Ответ: 32768 слов. Определим логарифмическую меру, позволяющую вычислять количество информации в битах. Такую информационную емкость (I) называют мерой Хартли: I = log 2 N = n log 2 q . Другими словами количество информации, полученное при выборе одного предмета из N равнозначных предметов, равно log 2 N. То есть именно такое количество информации необходимо для устранения неопределенности из N равновозможных вариантов. Задача 2. Чему равно количество информации для трехбуквенных русских слов? Решение Для трехбуквенных русских слов I = 3 log2 32 = 15 (бит). Ответ: 15 бит. Значение I – количество двоичных разрядов. Оно не может быть дробным, поэтому в случае получения дробного значения, необходимо округлить результат. Итак, 1 бит информации соответствует одному элементарному событию, которое может произойти или не произойти. Такая мера количества информации удобна тем, что она позволяет оперировать мерой как числом. Количество информации при этом эквивалентно количеству двоичных символов 0 или 1. Закон аддитивности информации: при наличии нескольких источников информации общее количество информации равно 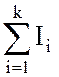 I = I 1 + I 2 + … + I k = где Ii – количество информации от источника i. Всего источников – k. Задача 3. Используя закон аддитивности и формулу Хартли, подсчитайте, какое количество информации несет достоверный прогноз погоды. Решение. Предположим, что прогноз погоды на следующий день заключается в предсказании дневной температуры (обычно выбор делается из 16 возможных для данного сезона значений) и одного из четырех значений облачности (солнечно, переменная облачность, пасмурно, дождь). Получаемое при этом количество информации равно I = log216 + log24 = 4 + 2 = 6 (бит) Ответ: 6 бит. Логарифмическая мера информации позволяет измерить количество информации и используется на практике. Задача 4. Определить, какое количество информации в битах содержит книга, написанная на русском языке, содержащая 200 страниц (каждая страница содержит приблизительно 2000 символов). Решение Для решения воспользуемся мерой Хартли: I = n log 2 q = 200 ∙ 2000 ∙ log 2 32 = 2000000 бит. Здесь n – длина сообщения в знаках: n = 200 страниц ∙ 2000 знаков/страница = 400000 знаков. Ответ: 2000000 бит. | ||||||
| | Заполните таблицу:
Обсудите заполненную таблицу с другими студентами группы. Как вы теперь ответите на вопрос: «Можно ли измерить информацию? Если да, то как?». Существуют ли ситуации, когда количественное выражение информации не позволяет определить ее значимость для человека, общества? | |||||
| | Решите следующие задачи:
|