Представление числовых данных в компьютерных системах

БАЗОВЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ КОМПЬЮТЕРНОЙ АРИФМЕТИКИ

Компьютерная арифметика - совокупность принципов и форм представления числовой информации, методов и алгоритмов выполнения арифметических операций и вычисления элементарных функций, рассматриваемых на уровне внутренней структурной организации технических средств компьютерных систем ( КС ). Это часть вычислительной математики, ориентированной на логический уровень описания вычислительных структур и процессов в них.

Что такое информация вообще, в общем понимании? Термин информацияпроисходит от латинского слова information,что означает:

- сведения;

- разъяснения;

- изложение.

Алгоритм — способ преобразования информации, который задается с помощью конечной системы правил. Информация представляется в виде совокупности цифр (чисел) в некоторой системе счисления, сами же цифры отображаются сигналами, имеющими конечное число уровней квантования.

Система счисления (СС) - совокупность приемов и правил для установления однозначного соответствия между любым числом и его представлением в виде некоторой совокупности знаков (символов).

Количественный эквивалент числа (КЭЧ) - некоторое количество, однозначно соответствующее числу. (На абстрактно-интуитивном уровне безотносительно к системам счисления и измерения). Каждой цифре в записи числа сопоставляется некоторое количество, выражаемое этой цифрой и называемое количественным эквивалентом цифры (КЭЦ).

Длина числа - количество позиций (разрядов) в записи числа. В техническом аспекте длина числа интерпретируется как длина разрядной сетки (ДРС). Для разных СС характерна различная ДРС, необходимая для записи одного и того же числа.

Все операции в КС выполняются как последовательности в пространстве и во времени некоторых простейших, элементарных операций, называемых микрооперациями. К числу основных классов микроопераций относятся:

1) передача (прием, выдача) операнда;

2) сдвиг (арифметический, циклический, логический, модифицированный) операнда на заданное число разрядов;

3) прибавление к операнду или вычитание из него единицы (в более общем случае - некоторой постоянной величины);

4) сравнение операндов (по принципу "больше - меньше - равно");

5) поразрядные логические операции (дизъюнкции, конъюнкции, равнозначности, сложения по модулю 2);

6) арифметическое сложение двух операндов, соответствующих числам в одной и той же системе счисления;

7) преобразование кодов операндов (включая инверсию, дополнение, шифрацию, дешифрацию и др.).

СИСТЕМЫ СЧИСЛЕНИЯ

Как было отмечено в первой главе система счисления - совокупность приемов и правил для установления однозначного соответствия между любым числом и его представлением в виде некоторой совокупности знаков (символов). Запись числа в некоторой системе счисления называют кодом числа. Кратко число записывается следующим образом:

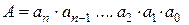. (2.1)

где: А – количественный эквивалент числа (А);

( a_na_n-1….a₂a₁a₀ ) - цифры из множества, с помощью которых можно представить число (А).

Отдельную позицию в изображении числа принято называть разрядом, а номер позиции - номером разряда. Число разрядов в записи числа называется разрядностью и совпадает с его длиной. В техническом аспекте длина числа интерпретируется как длина разрядной сетки. Если алфавит имеет (p) различных значений, то разряд (а_i) в числе рассматривается как (р-ичная) цифра, которой может быть присвоено каждое из (р) значений. Каждой цифре (а_і) числа (А) однозначно соответствует ее количественный (числовой) эквивалент - (К(а_і)). Количественный эквивалент числа - (КЭЧ) - (А), заданного в определенной системе счисления, является некоторой функцией числовых эквивалентов всех его цифр, т.е.:

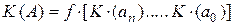. (2.2)

где: К(А) - количественный эквивалент числа (А);

К (а_n) – максимальный количественный (числовой) эквивалент цифры числа (А), находящийся в крайнем левом разряде;

К (а₀) – минимальный количественный (числовой) эквивалент цифры числа (А), находящийся в крайнем правом разряде;

Тогда при любой конечной разрядной сетке КЭЧ (А) будет принимать в зависимости от количественных эквивалентов отдельных разрядов значения от К(А)_min до К(А)_max. Диапазон представления (D) чисел в данной системе счисления - это интервал числовой оси, заключенный между максимальными и минимальными числами, представленными заданной разрядностью ( длинной разрядной сетки):

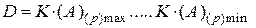. (2.3)

где: D - диапазон представимых чисел в определенной системе счисления;

К(А)_(р)max - максимальный количественный эквивалент числа (А) по основанию (р);

К(А)_(р)mіn - минимальный количественный эквивалент числа (А) по основанию (р).

Любая система счисления, предназначенная для практического использования, должна обеспечивать: - возможность представления любого числа в заданном диапазоне чисел; - однозначность представления; - краткость и простоту записи чисел; - легкость овладения системой, а также простоту и удобство оперирования ею.

2.1 Классификация систем счисления

В настоящее время различают позиционныеи непозиционные системы счисления. Классификация систем счисления приведена на рис. 2.1.

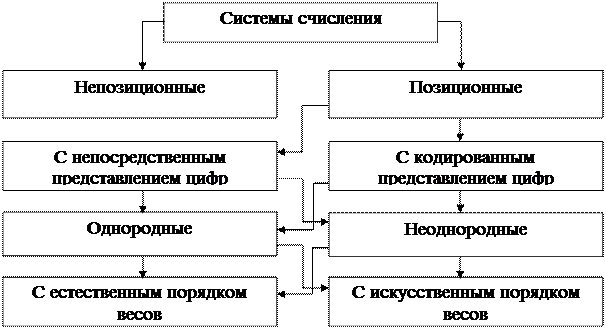Рисунок 2.1 — Классификация систем счисления

Непозиционная система счисления: это такая система счисления, в которой каждой цифре на любом ее месте в записи числа однозначно соответствует один и тот же количественный эквивалент.

Наиболее известным примером такой системы является римская система счисления, рис. 2.2, например:

Десятичные числа:
Римские цифры:	I	V	X	L	C	D	M

Рисунок 2.2 - Соответствие десятичных чисел римским цифрам

В римской системе счисления несколько стоящих рядом одинаковых цифр суммируются рис.2.3:

XXX = X+X+X= 30₍₁₀₎.

Рисунок 2.3 – Пример записи числа с основанием (10) в Римской системе счисления

Если рядом стоят разные цифры, причем младшая – справа от старшей, то они также суммируются, рис.2.4:

XVI = X+V+I = 16₍₁₀₎.

Рисунок 2.4 – Пример записи числа с основанием (10) в Римской системе счисления

Если же младшая цифра находится слева от старшей, то она вычитается из этой старшей цифры рис.2.5:

IX = X – I = 9₍₁₀₎.

Рисунок 2.5 – Пример записи числа с основанием(10) в Римской системе счисления

Недостатки римской системы счисления заключаются в следующем:

- в пределе, теоретически, она имеет бесконечное количество цифр;

- арифметические действия над числами очень сложны;

- отсутствует цифра {0}.

Позиционная система счисления:это такая система счисления, в которой одной и той же цифре в зависимости от ее местоположения в записи числа соответствуют различные количественные эквиваленты. Наиболее известным примером такой системы является десятичная система счисления, например: цифры 1 и 2 в зависимости от местоположения этих цифр в числе изменяется значение самого числа рис.2.6:

Разряды:	Десятки	Единицы
Цифры:

Рисунок 2.6 – Пример записи числа в десятичной системе счисления

При таком положении цифр получается число двенадцать (12₍₁₀₎). Нижний индекс при записи числа обозначает основание системы счисления, в данном случае (₍₁₀₎) означает десятичную систему счисления. Если поменять местами цифры 1 и 2, рис.2.7:

Разряды:	Десятки	Единицы
Цифры:

Рисунок 2.7 – Пример записи числа в десятичной системе счисления

получается число двадцать один (21₍₁₀₎). Для определения количественного эквивалента полной записи числа в позиционной системе счисления используется некоторая функция от количественных эквивалентов цифр. Если этой функцией является функция сложения, то систему называют аддитивной, если же используется функция умножения - систему называют мультипликативной.

Любое число в позиционной системе счисления может быть записано в виде:

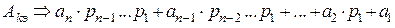. (2.4)

где 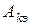- количественный эквивалент числа (А), состоящего из (n) цифр;

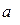- цифра, ;

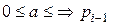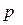- основание системы счисления.

В левой части равенства записано символическое изображение числа.

В правой части равенства показано, что все цифры числа в разных позициях имеют разный вес, при этом каждая позиция с присвоенными ей номером и весом называется – разрядом числа.

Правило: Количественный эквивалент числа в позиционной системе счисления равен сумме произведений количественных значений цифр и степеней основания, показатели которых равны номерам разрядов, причем нумерация разрядов начинается с (0).

Например: 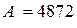, n=4, p=10, тогда можно записать:

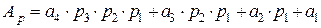. (2.5)

тогда:

.

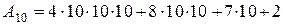Однородность системы счисления означает, что во всех разрядах числа, записанного в такой системе, используют цифры из одного и того же множества.

Например, в обычной десятичной системе счисления во всех разрядах числа используются цифры из множества рис.2.8:

{0,1,2,3,4,5,6,7,8,9},

Рисунок 2.8 – Множество цифр использующихся в десятичной системе счисления

в двоичной системе счисления используются цифры из множества рис.2.9:

{0,1},

Рисунок 2.9 – Множество цифр использующихся в двоичной системе счисления

в троичной системе счисления используются цифры из множества рис.2.10:

{0,1,2},

Рисунок 2.10 – Множество цифр использующихся в троичной системе счисления

в пятеричной системе счисления используются цифры из множества рис.2.11:

{0,1,2,3,4},

Рисунок 2.11 – Множество цифр использующихся в пятеричной системе счисления

в восьмеричной системе счисления используются цифры из множества рис.2.12:

{0,1,2,3,4,5,6,7},

Рисунок 2.12 – Множество цифр использующихся в восьмеричной системе счисления

в шестнадцатеричной системе счисления при записи числа используются цифры и буквы рис.2.13:

{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}.

Рисунок 2.13 – Множество цифр и букв использующихся в шестнадцатеричной системе счисления

Если позиционная система счисления однородная с непосредственным представлением цифр и с естественным порядком весов, то любое число может быть представлено в виде суммы попарных произведений:

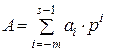. (2.6)

где 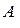- количественный эквивалент числа (А);

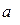- цифра,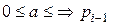

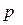- основание системы счисления.

s – количество разрядов в целой части числа слева от запятой;

m – количество разрядов в дробной части числа справа от запятой.

Исходя из выше сказанного можно записать:

.

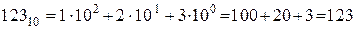или: .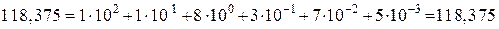

Соответствие чисел в (10 - ой), (16 – ой), (8 – ой) и (2 – ой) системах счисления приведены в табл. 2.1.

Таблица 2.1 - Соответствие чисел в (10 - ой), (16 – ой), (8 – ой) и (2 – ой) системах счисления

Десятеричная Х(10)	Шестнадцатеричная Х(16)	Восьмеричная Х(8)	Двоичная Х(2)
	А
	В
	С
	D
	Е
	F

Помимо позиционных однородных систем известны также позиционные неоднородные (смешанные) системы счисления.

В таких системах цифры в разных разрядах могут принимать значения из различных множеств.

Задают неоднородные системы с помощью двухстрочных матриц вида:

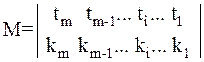. (2.7)

Здесь в первой строке матрицы указано число разрядов (t_i), отводимых в (i-й) группе разрядов (i= 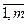) представления числа для записи цифр по основанию (k_i), которое указано во второй строке того же столбца.

Неоднородные системы счисления, так же как и однородные, могут быть с непосредственным и с кодированным представлением цифр.

Примером смешанной системы с кодированным представлением цифрявляется система измерения времени (в годах, месяцах, неделях, сутках, часах, минутах и секундах).

Например: надо выразить время в 2- года, 25 – суток, 14 – часов, 35 – минут и 48 секунд, в секундах. Тогда можно записать, что основание в каждом разряде равно:

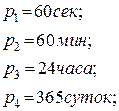
цифры имеют следующие значения:

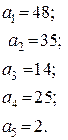
По формуле (2.4) можно записать:

.

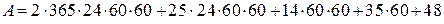Существует так же неоднородная двоично-пятиричная система счисления, в которой в нечетных разрядах основание р₁=5,(а_і= 0 – 4), а в четных разрядах основание р₂=2,(а_і= 0,1).

Так как произведение весов двух соседних (четного и нечетного) разрядов равно десяти, то двумя двоично-пятиричными разрядами можно кодировать одну десятичную цифру.

Пример записи десятичных цифр от 0 до 9 в двоично-пятиричной системе приведен в табл. 2.2.

Таблица 2.2 - Пример записи десятичных цифр в двоично-пятиричной системе

а(10)	а(2-5)	а(10)	а(2-5)

Например: записать число 853₍₁₀₎ в двоично-пятиричной системе счисления.

Решение: исходя из значений, представленных в табл. 2.2 имеем:

8(10)=13(2-5)

5(10)=10(2-5)

3(10)=03(2-5)

тогда: А₍₁₀₎ = 131003_(2-5).

Существует так же кодированные системы счисления – это позиционные системы счисления, в которых цифры одной системы счисления кодируются при помощи цифр другой системы, а число в общем виде записывается следующим образом:

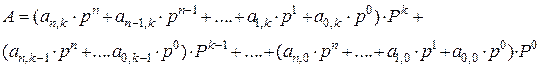. (2.8)

где: А - число;

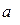- цифра;

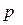- основание системы счисления, символами которой кодируются цифры;

Р – основание исходной системы счисления.

Классическим примером кодированной системы счисления есть – двоично-десятичная система.

При двоично-десятичном кодировании каждая десятичная цифра заменяется тетрадой (четверкой) двоичных цифр, а сами тетрады записываются последовательно в соответствии с порядком следования десятичных цифр.

При обратном преобразовании двоично-десятичного кода в десятичный исходный код разбивается на тетрады вправо и влево от запятой, которые затем заменяются десятичными цифрами.

Таким образом, при двоично-десятичном кодировании фактически не производится перевод числа в новую систему счисления, а мы имеем деле с двоично-кодированной десятичной системой счисления.

Например: десятичное число 12₍₁₀₎ записать в двоично-десятичной системе счисления = 00010010_(2-10).

При построении кодированных позиционных систем счисления в качестве весов разрядов могут быть выбраны как члены геометрической прогрессии, так и произвольные числа.

В зависимости от этого кодированные системы счисления делятся на кодированные системы счисления с естественными разрядами весов и на кодированные системы счисления с искусственными разрядами весов.

Кодированные системы счисления с естественными разрядами весов – это позиционная система счисления, в которой в качестве весов разрядов используются члены геометрической прогрессии.

Примером системы счисления с естественными разрядами весов может служить двоично-десятичная система с весами (8-4-2-1).

Кодированные системы счисления с искусственными разрядами весов – это позиционная система счисления, в которой в качестве весов разрядов используются произвольные числа.

Примером системы счисления с искусственными разрядами весов может служить двоично-десятичная система с весами (2-4-2-1, 5-2-1-3).

Искусственный порядок весов широко применяется в аналогово-цифровых и цифро-аналоговых преобразователях.

В табл. 2.3 представлены числа, записанные в десятичной системе счисления и в кодированной системе счисления с естественным и искусственным порядком весов.

Таблица 2.3 – Числа десятичной системы счисления и кодированной системе счисления с естественным и искусственным порядком весов.

Десятичная СС	Кодированная СС 8-4-2-1	Кодированная СС 4-2-2-1	Кодированная СС 2-4-2-1

Например: десятичное число 1593₍₁₀₎ в двоично-десятичной системе счисления с естественными разрядами весов 8-4-2-1 имеет вид: 0001 0101 1001 0011, а в двоично-десятичной системе счисления с искусственными разрядами весов 2-4-2-1 имеет вид: 0001 0101 1111 0011.

В современных компьютерных системах помимо рассмотренных систем счисления встречаются и системы счисления с непостоянными разрядами весов. Наиболее известным примером таких систем является код Грея.

Кодом Грея порядка (n) называется любая циклическая последовательность всех наборов из (0) и (1) длины (n), в которой два соседних набора отличаются ровно в одной компоненте.

Код Грея является одношаговым кодом, т.е. при переходе от одного числа к другому всегда меняется лишь какой то один из всех битов. Соответствие десятичных чисел в диапазоне от 0 до 15 двоичным числам и коду Грея приведено в табл. 2.4.

В двоичном коде при переходе от изображения одного числа к изображению соседнего числа может происходить одновременное изменение цифр в нескольких разрядах, что может явиться источником ошибок, в работе аппаратуры в некоторых случаях например при переходе от 7 к 8.

В коде Грея два соседних значения отличаются только в одном разряде.

Двоичные разряды в коде Грея не имеют постоянного веса. Код Грея изначально предназначался для защиты от ложного срабатывания электрических переключателей. Сегодня код Грея широко используется для упрощения выявлений и исправления ошибок в системах связи.

Таблица 2.4 - Соответствие десятичных чисел в диапазоне от 0 до 15 двоичным числам и коду Грея

Десятичные числа	Двоичные числа	Код Грея

2.2 Выбор системы счисления для использования в компьютерной системе

Непозиционные системы счисления непригодны в силу своей громоздкости и трудности выполнения арифметических операций.

Из позиционных систем счисления наиболее удобны однородные системы счисления, так как одинаковое основание, т.е. одинаковое количество символов во всех разрядах приводит к наиболее рациональному использованию оборудования и наиболее простым алгоритмам выполнения арифметических операций. Поэтому проанализируем однородные позиционные системы счисления на предмет их применения в компьютерных системах. При этом будем учитывать следующие факторы:

- простота технической реализации. Очевидно, что (р - позиционный) запоминающий элемент будет тем проще, чем меньше состояний (позиций) ему требуется иметь, т.е. чем меньше основание системы счисления.

- наибольшая помехоустойчивость кодирования цифр. Исходя из условия равных технических возможностей при реализации любой системы счисления, будем считать, что диапазон изменения носителя информации для всех систем остается одинаковым. Если увеличить диапазон некоторого носителя информации при реализации одной системы счисления, то его можно увеличить и при реализации другой системы. Но тогда очевидно преимущество систем с малыми основаниями, так, как представления цифр в этих системах отличаются друг от друга в более значительной степени, чем в системах с большими основаниями. Это значит, что при наложении на основной сигнал, изображающий цифру, некоторой помехи произвольной формы, наибольшая ошибка возможна в устройстве, использующем систему счисления с самым большим основанием.

- минимум оборудования. Чтобы решить, какой системе отдать предпочтение с точки зрения получения минимума расхода оборудования при прочих равных условиях, сделаем предположение, что все машины оперируют с одним и тем же количеством чисел. Если (b_i) – количество цифр, с которыми оперирует (i-я) машина; (n_i) – количество разрядов, в каждом числе (i-ой) машины, то произведение:

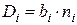. (2.9)

где D_i — количество цифроразрядов, приходящихся на 1 число;

b_i — количество цифр;

n_i — количество разрядов.

Таким образом, задача в данном случае сводится к нахождению такой системы счисления, которая имеет самое малое количество цифроразрядов при заданном количестве чисел – операндов (N):

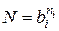. (2.10)

формулу (2.10) можно переписать в другом виде:

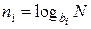. (2.11)

подставив это значение (n_i) в соотношение (2.9), получим:

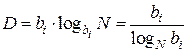. (2.12)

будим считать, что основание системы счисления может принимать любые значения, не только целочисленные, изменяясь непрерывно а не дискретно.

Тогда количество цифроразрядов также будет величиной непрерывной, связанной с основанием системы счисления логарифмической функциональной зависимостью:

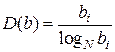. (2.13)

теперь задача нахождения D(b)_min.сводится к обыкновенному исследованию функции (2.13) на экстремум:

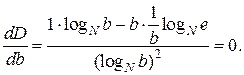(2.14)

откуда 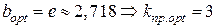. Выясним теперь, насколько каждое из целочисленных оснований (b_i) уступает (b_opt) Для этого оценим каждое основание (b_i) не абсолютной величиной (D_i), а его относительным значением:

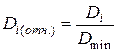. (2.15)

где:

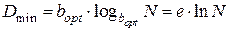(2.16)

Подставив выражение (2.16) в формулу (2.15), получим выражение, не зависящее от величины (N):

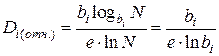. (2.17)

Произведя расчеты по формуле (2.17) для некоторых оснований системы счисления, сведем полученные результаты в табл. 2.5:

Таблица 2.5 – Соотношение оснований систем счисления и эффективности

bi
Di(отн.)	1,062	1,004	1,062	1,143	1,232	1,3	1,416	1,507	1,597

- простота арифметических действий. Чем меньше цифр в системе счисления, тем проще арифметические действия. Таблицы сложения, вычитания, умножения и деления будут усложняться с увеличением основания системы счисления.

- наибольшее быстродействие. Более сложные операции такие как умножение и деление, расчленяются на более простые операции такие как операции сложения и сдвига. С увеличением основания системы счисления быстродействие будет падать.

- простота формального аппарата для синтеза цифровых устройств.

Математическим аппаратом, позволяющим относительно просто и экономично строить цифровые схемы, узлы, блоки, является алгебра логики.

Наибольшее развитие и законченность вследствие своей простоты и широкого практического распространения двухпозиционных элементов в настоящее время получила двузначная логика.

- удобство работы.Безусловно наилучшейсистемой счисления с точки зрения удобства работы человека является десятичная, так как в любом другом случае потребуется переводить исходные числа из десятичной системы в принятую, а затем обратно в десятичную. Поэтому можно утверждать, что все системы счисления с основаниями превышающими десятичную систему счисления, являются менее удобными, чем системы с малыми основаниями.

В соответствии с рассмотренными критериями формируется комплексный показатель. При этом максимальную оценку получает система счисления с основанием два. Это позиционная система счисления, в которой для изображения чисел используются два символа, а веса разрядов меняются по закону ( ).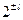

Большой практический интерес представляют двоично-кодированные системы счисления: двоично - десятичная Binary Code Decimal (BCD), восьмеричная (octal), шестнадцатеричная (hexadecimal). В них каждый разряд записывается с помощью нескольких двоичных разрядов, имеющих определенные веса. Цифры восьмеричной системы представляются тремя двоичными разрядами (триадами), десятичной и шестнадцатеричной - четырьмя (тетрадами). Также следует отметить, что восьме- и шестнадцатеричные системы относятся к особому классу систем с основанием кратным (2). Эта особенность обуславливает их широкое применение в процессе взаимодействия с пользователем компьютерной системы. С одной стороны, они облегчают восприятие двоичной информации, т.к. любое двоичное представление числа может быть разбито на триады или тетрады, которые проще для визуального восприятия человеком. С другой стороны, они часто используются в качестве промежуточных систем счисления при переводе из десятичной системы счисления в двоичную систему счисления и наоборот.

Двоичная система счисления вводит понятие основной структурной единицы информации, которой является бит (bit - binary digit). Бит соответствует одному двоичному разряду числа, представленного в двоичной системе счисления.

Однако бит является слишком мелкой единицей и не всегда удобен для практических приложений. Поэтому наряду с битом в компьютерной системе получила распространение производная структурная единица информации - машинное слово, под которым понимают упорядоченную совокупность битов, имеющую некоторый смысл, т.е. воспринимаемую основными устройствами компьютера как единое целое. Длина машинного слова является одной из определяющих характеристик компьютерной системы и выбирается исходя, прежде всего, из соображений точности. Таким образом, длина машинного слова является различной для компьютерных систем разных классов. Для унифицированного представления информации используют машинно-независимую структурную единицу - байт - byte - (кусок, часть) - совокупность из восьми смежных двоичных разрядов. Длину машинного слова обычно выбирают равной целому числу байт. Восьмиразрядный байт удобен тем, что полностью покрывает всю символьную информацию и удобен для записи десятичных и 16-ричных тетрад.

2.3 Перевод чисел из одной позиционной системы счисления в другую

Задача перевода чисел из одной позиционной системы счисления в другую является одной из главных в компьютерной арифметике. Ее можно сформулировать следующим образом: требуется перевести некоторое число (X), записанное в позиционной системе счисления с основанием (k₁), в такую же систему счисления, имеющую основание (k₂).

Другими словами: по изображению операнда (X) в системе счисления с основанием (k₁) найти изображение (Y) того же операнда в системе с основанием (k₂).

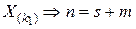. (2.18)

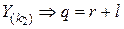. (2.19)

Существуют 2 группы методов перевода: табличные и расчетные.

1.Табличные методы. В простейшем случае в памяти компьютерной системы хранится таблица соответствия между всеми числами в системах счисления с основаниями (k₁) и (k₂), а сама процедура перевода сводится к обращению к этой таблице. Плюс табличных методов перевода заключается в высокой скорости перевода. Минус табличных методов перевода заключается в том, что размеры такой таблицы и, следовательно, занимаемый ею объем памяти, часто оказываются технически неприемлемыми. Поэтому с целью уменьшения занимаемого объема памяти в ней хранят только таблицы соответствия цифр заданных систем счисления и весов их разрядов. Перевод чисел осуществляется путем обращения к этим таблицам и выполнения операций умножения и сложения в соответствии с выражением для КЭЧ. Если, например, числа в системе с основанием (k₁) представлены (n – разрядами), то по первому варианту размерность таблицы, сохраняемой в памяти, определяется ( 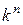) строками, а по второму варианту - (k₁+n+1) строками.

2.Расчетные методы. В общем виде решение задачи перевода можно представить как нахождение коэффициентов (y_j) нового ряда, изображающего число в системе счисления с основанием (k₂).

Тривиальным методом решения является. Основная трудность - в выборе максимальной степени ( 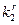), которая все еще содержится в числе (X).

Все действия должны выполняться по правилам (k₁-арифметики), т.е. по правилам исходной арифметики. После нахождения максимальной степени основания проверяют «вхождение» в заданное число всех степеней нового основания, меньших максимального. Каждая из отмеченных степеней может входить в ряд не более 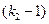раз, что определяется условием:

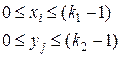(2.20)

Для перевода операнда (X) в систему с основанием (k₂) необходимо записать (X) в форме для вычисления количественного эквивалента, далее заменить цифры (x_i) и основания (k₁) их эквивалентами в системе с основанием (k₂), а потом вычислить полученное выражение по правилам арифметики в системе с основанием (k₂). Этот алгоритм удобно использовать в случае, когда (k₁<k₂), причем (k₂) соответствует системе счисления, где просто и "привычно" выполняются операции сложения и умножения (например, десятичной системе). Для упрощения вычислений при этом используют схему Горнера, в соответствии с которой формула для КЭЧ преобразуется путем многократного вынесения за скобки:

Y=(...((x_s-1k₁+x_s-2)k₁+x_s-3)k₁+...+x₁)k₁+x₀+…+(..(((0+x_-m) k₁^-1 +

+x_-m+1)k₁^-1+x_-m+2)k₁^-1+...+x_-1)k₁^-1. (2.21)

Отсюда видно, что для получения целой части числа необходимо выполнить (s) шагов вычислений, а для получения дробной - (m).

Т.е., алгоритм МНЗ, по существу, состоит из двух алгоритмов, а именно: перевода целого числа, выполняемого в соответствии с рекуррентной формулой

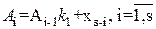(2.22)

где А₀=0, A_s - целая часть исходного числа в системе счисления с основанием (k₂); и перевода дробей по рекуррентной формуле:

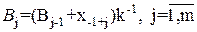(2.23)

где В₀=0, В_m - дробная часть исходного числа в системе с основанием

(k₂ ).

Рассмотренный алгоритм не имеет каких-либо теоретических ограничений на область своего применения.

Однако при переводе целых чисел в системы с "непривычными" основаниями, особенно в случае (k₁>k₂), использование этого алгоритма связано с весьма громоздкими вычислениями.

Поэтому на практике используют отдельные алгоритмы перевода целых чисел и правильных дробей.

В случае (k1>k2). Целое число (X) запишем в системе с основанием (k₂) с использованием схемы Горнера:

Y=(…((y_r-1k₂+y_r-2)k₂+y_r-3)k₂+…+y₁)k₂+y₀. (2.24)

Правую часть выражения разделим на величину основания (k₂). В результате получим первый остаток (y₀) и целую часть:

Y=(…((y_r-1k₂+y_r-2)k₂+y_r-3)k₂+…+y₁). (2.25)

Разделив целую часть на( k₂), найдем второй остаток( y₁).

Повторяя процесс деления r раз, получим последнее целое частное, которое, по условию, меньше основания системы счисления (k₂) и является старшей цифрой числа, представленного в системе с основанием (k₂).

Правило перевода целых чисел из одной позиционной системы счисления в другую:

- для перевода целого числа в новую систему его надо последовательно делить на основание новой системы счисления до тех пор, пока не получится частное, у которого целая часть равна (0).

Число в новой системе счисления записывается из остатков от последовательного деления, причем последний остаток будет старшей цифрой нового числа.

Алгоритмперевода целых чисел из одной позиционной системы счисления в другую можно сформулировать следующим образом: