Самоорганизующиеся сети кохонена

Характерной особенностью мозга является то, что его структура, по-видимому ,, отражает организацию внешних раздражителей, которые в него поступают. На пример, известно соответствие относительного положения рецепторов на поверхности кожи и нейронов в мозге, которые воспринимают и обрабатывают сигналы от этих рецепторов, а участки кожи, которые плотно «населены» рецепторами (лицо, руки), ассоциированы с пропорционально большим числом нейронов. Это соответствие образует то, что называется соматотропической ( somatotropic ) кар той, которая отражает поверхность кожи в часть мозга — соматосенсорную кору которая и воспринимает ощущение касания.

Системы, построенные на базе, например, многослойных сетей с обратным распределением ошибок имеют очевидный недостаток, заключающийся в том, что мы (как учитель) должны заранее заготовить входы и запастись соответствующими правильными ответами для обучения сети. Принципы функционирования природной соматотропической карты легли в основу создания самоорганизующихся сетей (карт, решеток) Кохонена , для которых не требуется предварительное обучение на примерах. Сеть Кохонена воспринимает только вход и способна вырабатывать свое собственное восприятие внешних стимулов.

Самоорганизующиеся сети Кохонена — это карты или многомерные решетки, d каждым узлом которой ассоциирован входной весовой вектор, то есть набор из k входных весов нейрона трактуется как вектор в n- мерном пространстве. (на рис. 6.5 представлена сеть при k = 2.) Входной весовой вектор имеет ту же размерность, что и вход в сеть. Обучение происходит в результате конкуренции, возникающей между узлами сети за право отклика на полученный входной сигнал. Элемент сети, который выигрывает в этой конкуренции (победитель), и его ближайшее окружение (свита) модифицируют веса своих входных связей. Перед обучением каждая компонента входного весового вектора инициализируются случайным образом. Обычно каждый вектор нормализуется в вектор с единичной длиной в пространстве весов. Это делается делением соответствующего веса на корень из суммы квадратов компонент этого весового вектора. Входные вектора нормализуются аналогично. Обучение сети состоит из следующих этапов:

1. Вектор х = (х ₁ , х₂,..., x_k ) подается на вход сети.

2. Определяется расстояние d_ij (в k -мерном пространстве) между х и весовыми векторами _ij каждого нейрона, например: d_tj =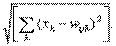

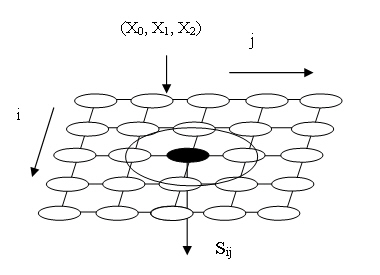
Рис. 6.5. Самоорганизующаяся карта Кохонена

3. Нейрон, который имеет весовой вектор, самый близкий к х , объявляется «победителем». Этот весовой вектор 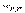становится основным в группе входных весовых векторов, которые лежат в пределах расстояния D от 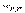. Таким образом определяется "свита" победителя.

4. Группа входных весовых векторов модифицируется (поощряется) в соответствии со следующим выражением 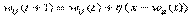для всех весовых векторов в пределах расстояния D от .

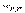5. Шаги 1 — 4 повторяются для каждого входного вектора.

В процессе обучения значения D и постепенно уменьшаются: η : 1 → 0, D в начале обучения может равняться максимальному расстоянию между весовыми векторами, а к концу обучения доходить до величины, при которой будет обучаться толь ко один нейрон.

Из формулы адаптации входного весового вектора следует, что он (для победите ля и его «свиты») сдвигается по направлению к входному вектору. Таким образом, по мере поступления новых входных векторов весовые векторы сети разделяются на группы, формирующиеся в виде облаков (сгустков, кластеров) вокруг входных векторов. По мере обучения плотность весовых векторов будет выше в тех позициях пространства, где входные векторы появляются чаще, и наоборот. В результате сеть Кохонена адаптирует себя так, что плотность весовых векторов будет соответствовать плотности входных векторов. Так, если, например, на вход сети подать поток равномерно распределенных случайных величин, то сетевые веса будут самоприводиться в порядок в регулярную решетку. На рис. 7.6 приведен пример самообучения двухмерной сети Кохонена.

В общем случае h = h ( r , t ), где г — расстояние между нейронами, f — параметр, характеризующий время обучения. Эта функция традиционно имеет вид «мексиканской шляпы» (зависимость силы связи от расстояния до победителя), которая по мере увеличения параметра f делается более узкой.

Обучающий алгоритм настраивает входные весовые векторы в окрестности возбужденного нейрона таким образом, чтобы они были более «похожими» на вход ной вектор. Если все векторы нормализованы в векторы с единичной длиной, то они могут рассматриваться как точки на поверхности единичной гиперсферы . В процессе обучения группа соседних весовых точек перемещается ближе к точке входного вектора.

Очевидно, так как S = 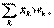то победитель может быть найден так:

( i ^* , j ^* ) = arg max ( S_ij ) — наиболее активный нейрон.

Самоорганизующиеся сети, как уже отмечалось, не требуют предварительного обучения на примерах (учитель не нужен) и используются в задачах распознавания — классификации образов, представленных векторными величинами, в которых каждая компонента вектора соответствует элементу образа. После обучения подача входного вектора из данного класса будет приводить к возбуждению нейронов; тогда нейрон с максимальным возбуждением и будет представлять классификацию. Очевидно, в общем случае можно формировать выход, зависящий как от активности победителя, так и от его свиты. Так как обучение проводится без указания целевого вектора, то априори невозможно определить, какой нейрон будет соответствовать данному классу входных векторов. Однако после обучения такие соответствия легко идентифицируются и могут быть использованы, например, в задачах управления.