Арифметико-логическое устройство
↑ Наверх
Арифметико-логическое устройство (АЛУ) – важнейшая часть процессора. Оно позволяет выполнять разнообразные арифметические и логические операции над операндами. Вид выполняемой в АЛУ операции определяет программист, составляющий управляющую программу. Программа, хранящаяся в оперативной памяти, по частям передается в процессор, где и выполняется. Таким образом, процессор лишь исполняет указания программиста, выраженные в виде совокупности команд (программы).
Процессор (как и все другие цифровые устройства) воспринимает управляющие сигналы и операнды в виде двоичных чисел. Результат также формируется в виде двоичных чисел. Однако программисты составляют управляющие программы чаще всего на языках программирования высокого уровня (Паскаль, Бейсик, Си…). В момент трансляции программы ее текст превращается в набор двоичных чисел (объектный код). Именно эти двоичные числа заставляют процессор (в том числе и АЛУ) выполнять операции, запланированные программистом.
Структурная схема простейшего АЛУ показана на рис. 8.2.
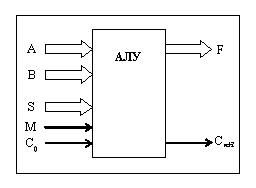
Рис. 8.2. Структурная схема простейшего АЛУ
Два многоразрядных операнда (числа, буквы, символы и т.д.), подлежащие обработке в АЛУ, подаются на входы А и В. Результат выполнения операции появляется на выходе F. Вид операции, выполняемой в АЛУ, определяется сигналами, которые подаются на входы S и M. Таким образом при сложении чисел 2 и 3 одно из них подается на вход А, а второе – на вход В. В этот момент на шины S и М подается двоичное число, которое на обыденном языке означает команду (приказ) «Выполнить арифметическое сложение». Результат сложения – число 5 появляется на выходе F.
У входов M и S одинаковое назначение – определять вид выполняемой в АЛУ операции. Эти входы разделены лишь с методической целью. Сигнал на входе М (Mode – режим) определяет, какую операцию будет выполнять АЛУ – логическую или арифметическую.
Рассматриваемый простейший тип АЛУ (К155ИП3, американский аналог – 74181) имеет малую разрядность – лишь 4 бита. По этой причине разработчики АЛУ предусмотрели возможность увеличения (наращивания) разрядности устройства (в случае возникновения такой необходимости). Увеличить разрядность АЛУ можно за счет использования нескольких секций (микросхем) и двух специальных шин C0 и Cn+1.
Шина C0 при создании многоразрядных конструкций используется для приема переноса, формируемого в предыдущей (младшей) секции (микросхеме). Шина Cn+1 служит для передачи арифметического переноса из младшей секции в старшую. Другими словами: если у разработчика в наличии имеется n-разрядное АЛУ, то для получения разрядности 2n нужно взять еще одну аналогичную микросхему, объединить параллельно входы S и M, а выход Cn+1 младшей секции соединить со входом C0 старшей секции (микросхемы). Логические и арифметические операции отличаются тем, что в логических операциях вычисления производятся поразрядно (между собой взаимодействуют только одноименные разряды и переносов между разрядами нет). При выполнении арифметических операций в случае необходимости происходят переносы между соседними разрядами (от младшего разряда к старшему).
Проиллюстрируем сказанное двумя примерами: логической операцией Исключающее ИЛИ и арифметическим сложением. Обе операции выполняются по одинаковым правилам, но в арифметическом сложении допускается перенос между разрядами.
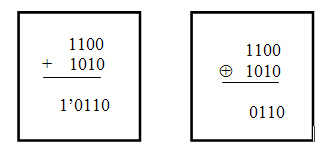
Рис. 8.3. Логические операции Исключающее ИЛИ и арифметическое сложение
Предположим, что имеется два десятичных числа A = 12D и B = 10D. В двоичной системе счисления эти числа имеют вид: A =1100B и B =1010B.
В результате выполнения логической операции Исключающее ИЛИ получается четырехразрядное число 0110B. После выполнения арифметического сложения на выходе F появляется четырехразрядное число 0110B, а на шине Cn+1 присутствует логическая единица. Этот сигнал свидетельствует о возникновении переноса в пятый разряд, т. е. в следующую старшую секцию восьмиразрядного АЛУ.
Работу четырехразрядного АЛУ можно описать выражением:
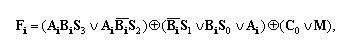
В этой формуле индексами i отмечены номера разрядов операндов A и B и выходного сигнала F.
Если на управляющие входы такого АЛУ подать сигналы M = 1, S3 = 1, S2 = 0, S1 = 1, S0 = 1, то АЛУ будет выполнять операцию Fi = Ai ^ Bi, т. е. операцию конъюнкции (логическое умножение). Этот результат получается при подстановке исходных данных в приведенную формулу.
Изменяя пять управляющих сигналов M, S3,…S0, можно «заставить» такое АЛУ выполнить 32 различные операции (16 логических и 16 арифметических).
Так, присутствие на управляющих входах двоичного числа M = 0, S3 = 1, S2 = 0, S1 =0, S0 = 1 заставит АЛУ выполнить арифметическое сложение чисел, поступивших на шины A и B, и к полученному результату прибавить значение переноса из предыдущей секции, т. е. Fi = Ai + Bi + C0.
В табл. 8.2. показано, как, изменяя управляющие сигналы, можно задавать вид выполняемой операции.
Таблица 8.2. Иерархия процессоров и их характеристики
| Управляющие сигналы | Выполняемые операции | ||||
| S3 | S2 | S1 | S0 | Логические М = 1 | Арифметические М = 0 |
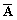 | A + C0 | ||||
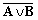 | (A v B) + C0 | ||||
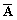 ^ B ^ B | (A v 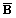 ) + C0 ) + C0 | ||||
| 1111 + C0 | |||||
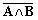 | A + (A ^ 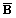 ) + C0 ) + C0 | ||||
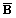 | (A v B) + (A ^ 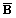 ) + C0 ) + C0 | ||||
 | A + 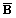 + C0 + C0 | ||||
A ^ 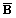 | 1111 + (A ^ 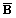 ) + C0 ) + C0 | ||||
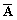 v B v B | A + (A ^ B) + C0 | ||||
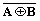 | A + B + C0 | ||||
| B | (A v 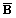 ) + (A ^ B) + C0 ) + (A ^ B) + C0 | ||||
| A ^ B | 1111 + (A ^ B) + C0 | ||||
| A + A + C0 | |||||
A v 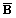 | (A v B) + A + C0 | ||||
| A v B | (A v 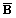 ) + A + C0 ) + A + C0 | ||||
| A | 1111 + A + C0 |
