Логика высказывани и предикатов

Логическое высказывание – связанное повествовательное предложение, о котором можно сказать истинно оно или ложно (На улице идёт дождь – высказывание, какая хорошая погода – не высказывание). В логике высказываний нас интересует не содержание, а истинностное значение высказываний (0 – Ложь, 1 – Истина).

Высказывания А и В равносильны тогда и только тогда, когда истинностные значения А и В совпадают ( ).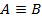

Основные операции над логическими высказываниями: (см. вопрос 2.1).

Логика предикатов – логическая система, средствами которой можно исследовать структуру высказываний.

Предикат – свойство объекта (отношения между объектами). Быть чётным, быть простым, делиться, быть больше.

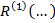– унарный.

– бинарный.

– трёхместный.

Предикат – функция, высказывательные переменные которой принимают значения из некоторого множества , а сама функция принимает значения {0; 1}.

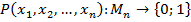
Для задания предиката должно быть задано:

1. Область определения , состоящая из множества предметных переменных.

2. Множество 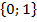– область значений предиката.

3. Правило, по которому каждому элементу из множества ставится в соответствие элемент из множества .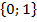

Способы задания предиката.

1. Графический.

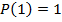
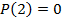
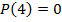
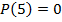
2. Табличный

3. Словесный

Предикат выполняется при и не выполняется во всех остальных точках x области определения.

4. Формульный (аналитический).

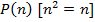
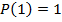
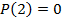
В логике предикатов для образования предложений можно использовать те же логические операции, что и в логике высказываний, т.е. дизъюнкцию, конъюнкцию, эквиваленцию, в результате получаются новые предикаты.

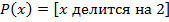
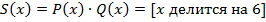
Кванторы.

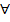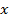1. Квантор общности. . Пусть – некоторый предикат, под выражением будем подразумевать высказывание, истинное когда истина для любого из множества и ложное в противоположном случае.

2. Квантор существования. . Пусть – некоторый предикат, под выражением будем подразумевать высказывание, истинное когда существует элемент из множества , для которого истинно и ложное в противоположном случае. 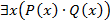. Существует такое x, которое кратно 2 и кратно 3.

Операции, уменьшающие местность предиката.

1. Фиксация значений переменной.

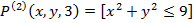
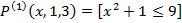
2. Операция связывания квантором

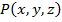
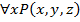
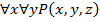
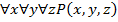
Обобщение логических операций с помощью квантора.

Пусть – одноместный предикат, который определён на конечном множестве 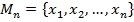. . 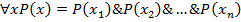Квантор общности определяет операцию конъюнкция.

Квантор существования обобщает операцию дизъюнкция.

Основные равносильности алгебры предикатов, содержащие кванторы.

1. Законы де Моргана. 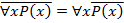, (перенос отрицания).

2. Перестановка одноимённых кванторов (коммунитативные законы). , .

3. Дистрибутивные законы. ,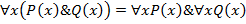

4. Законы ограничения действия кванторов , , , .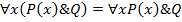

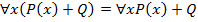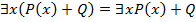Все законы, которые работают в алгебре высказываний, переносятся в алгебру предикатов.