Удаление невидимых линий и поверхностей

Первые публикации алгоритмов удаления невидимых элементов изображения появились сравнительно недавно, в начале 70-х годов. Первый из опубликованных алгоритмов имел номер 420. Это говорит о том, что существует много различных подходов к решению этой задачи. Необходимость удаления невидимых частей изображения связана с тем, что по каркасному изображению объектов невозможно определить, как выглядит сцена, как расположены объекты. Например:

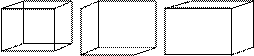
Рис. 76

Известные алгоритмы удаления невидимых линий и поверхностей можно разделить на три группы по типу пространства, в котором производится анализ видимости элементов изображения:

1)объектные,

2)картинные,

3)смешанные.

Кроме того, различные алгоритмы ориентированы на определенный способ задания поверхностей. Поверхность может быть задана аналитически, в виде совокупности многоугольных граней, в виде совокупности частей, каждая из которых задается аналитически.

Все алгоритмы, но каждый по-своему, решают задачу загораживания. Рассмотрим некоторые принципы, используемые при решении задачи загораживания.

1.Пусть сцену можно разбить на два фрагмента. Самые дальние точки одного из них ближе к наблюдателю, чем самые ближние точки другого. В этом случае первый фрагмент не может быть загорожен вторым.

2.Если существует плоскость, проходящая так, что один из фрагментов сцены и наблюдатель находятся в одном полупространстве, а второй фрагмент - в другом, то первый фрагмент не может быть загорожен другим.

2.1.Если фрагменты выпуклы и не пересекаются, то такая плоскость существует всегда.

2.2.Если фрагменты не выпуклы, но могут быть заключены в выпуклые оболочки, для которых выполняется условие 2.1, то плоскость может быть построена.

3.Если проекции фрагментов на картинную плоскость не пересекаются, то ни один из фрагментов не может быть загорожен другим.

Общая задача нахождения пересечения проекций сложна. Иногда ее решение упрощается, если выполняется достаточное условие: непересечение оболочек проекций этих фрагментов (одномерных х и у-полос, прямоугольных и круговых). При выводе изображения выпуклого многогранника его каждая грань может быть или полностью видима или невидима.

Рассмотренные принципы позволяют определить порядок визуализации фрагментов. Если же для двух фрагментов уже определен порядок визуализации, но эти фрагменты сложны, то перечисленные принципы используются рекурсивно для каждого из фрагментов до тех пор, пока вывод фрагментов не представляет трудности.

Остановимся на некоторых алгоритмах поподробнее.

АЛГОРИТМ РОБЕРТСА

Алгоритм работает в объектном пространстве. Сцена представляет собой совокупность выпуклых многогранников, которые задаются своими вершинами, ребрами и гранями. Алгоритм использует ортогональное проектирование на плоскость z=0. Для получения центральной проекции предварительно сцену подвергают перспективному преобразованию. Удаление невидимых граней и ребер выполняется в два этапа.

На первом этапе для каждого тела удаляют грани и ребра, экранируемые самим телом. На втором этапе каждое из видимых ребер каждого тела сравнивается со всеми телами сцены для определения видимых частей ребра.

Если сцена содержит невыпуклые многогранники, то для применения метода Робертса они должны быть разбиты на выпуклые.

1 ЭТАП. Определение нелицевых (невидимых) граней и ребер выпуклого многогранника.

Выпуклый многогранник можно представлять набором плоскостей a_ix+b_iy+c_iz+d_i=0 (i=1,...,n), содержащих его грани. В векторном виде уравнение плоскости можно записать так : P·V_i =0, где

Р=(x, y, z,1),

Плоскость делит пространство на две части. Для всех точек одного из полупространств выполняется неравенство P·V_i >0, для другого - P·V_i <0. Приведем уравнения всех граней многогранника к виду, при котором для внутренних точек тела выполняется неравенство P·V_i >0, i=1,...,n. Будем использовать матрицу плоскостей

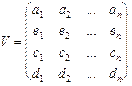такую, что P·V=(d₁, d₂, ...,d_n). Для точки внутри тела d_i>0, i=1,n. Для точки вне тела найдутся такие i, что d_i<0.

Так как производится ортогональное проектирование на z=0, центр проектирования находится в бесконечно удаленной точке (0,0,1,0). Для нелицевых граней должно выполняться условие существования j такого, что точке на плоскости z=-¥: (0,0,-1,0)×V_j<0 (V_j - j-тый столбец матрицы V). Это значит, что нелицевыми гранями являются те грани, у которых в уравнении плоскости с_j>0 (положительный элемент третьей строки).

Ребро является невидимым, если оно является общим ребром двух невидимых граней. Удобно для каждого ребра хранить не только номера вершин, являющихся его концами, но и номера граней, для которых это ребро является общим.

Описанный метод определения нелицевых граней часто используется как подготовительный этап для некоторых алгоритмов. В результате выполнения первого этапа имеем матрицы всех тел сцены и списки видимых ребер для каждого тела.

На втором этапе для каждого видимого ребра определяются видимые части при экранировании другими телами сцены.

Рассмотрим параметрическое уравнение ребра Р₁Р₂ : Р(t)=P₁+(P₂-P₁) ·t, tÎ[0;1]. Точка Р(t) не экранируется телом G, если луч, исходящий из этой точки в направлении центра проектирования (0,0,1) не пересекает тела G. Параметрическое уравнение луча:

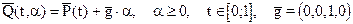
Вычислим где V - матрица плоскостей тела G. Если существует tÎ[0;1], a³0, что h_i >0 для всякого i=1,...,n (n - число граней G), то точка Р(t) невидима. Если h_i ³0 и существует j, что h_i =0, то точка Q(t, a) лежит на поверхности тела. Если при этом a=0, то имеем точку протыкания одного тела другим.

Таким образом, для нахождения невидимой части отрезка Р₁Р₂ необходимо решить две задачи линейного программирования.

Система ограничений:

Требуется найти минимум t и максимум t, при которых справедливы неравенства системы ограничений.

Отрезок Р(t_min)P(t_max) является невидимым. В списке видимых ребер заменяем ребро Р₁Р₂ его видимыми частям.

Если Р(t_min) и/или P(t_max) является точкой протыкания, нужно установить флаг протыкания и запомнить точки протыкания в списке точек протыкания.

При большом количестве граней рассмотренный алгоритм требует больших затрат времени. Но существует более простой метод определения полностью видимых отрезков. Введем обозначения

В этих обозначениях h_i =u_i+tv_i+aw_i. Для полностью видимых отрезков должны выполняться неравенства

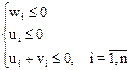(т.к. увеличив a,добьемся максимума и h_i>0)

(начальная точка: a=0, t=0)

(конечная точка: a=0, t=1)

Простых методов определения полностью невидимых отрезков нет.

Опишем алгоритм Робертса на втором этапе.

Определим для каждого тела минимальные объемлющие параллелепипеды с гранями, параллельными координатным плоскостям. Т.е. находим x_min, x_max, y_min, y_max, z_min, z_max . Упорядочиваем тела по неубыванию z_max в списке тел (первые в списке наиболее отдельные тела).

Цикл: Для каждого тела Т, начиная с первого в списке тел

Цикл: Для каждого тела S, начиная следующим за Т в списке

Если XY - оболочки тел Т и S пересекаются

Определяем видимые части ребер из списка видимых ребер тела Т при экранировании их телом S. Заменяем ребро его видимыми частями.

Если есть протыкание запоминаем точки протыкания в списке протыканий.

Если Z-оболочки тел Т и S пересекаются,

Определяем видимые части списка видимых ребер тела S при экранировании их телом Т. Заменяем эти ребра их видимыми частями.

Если есть точки протыкания, то заносим точки протыкания в список протыканий.

Если список протыканий не пуст;

Получаем список отрезков, соединяя всевозможные пары точек протыкания, и определяем видимые части каждого из этих отрезков при экранировании их телами Т и S. Заменяем каждый отрезок его видимыми частями.

Добавляем полученный список к списку видимых ребер тела.

Удаляем список протыканий.

Конец цикла для S.

Конец цикла для Т.

Цикл: Для каждого тела Т в списке тел

Выводим все ребра списка видимых ребер тела Т.

Конец цикла.

АЛГОРИТМ ВАРИОКА

Идея алгоритма основана на том, что большие части изображения однородны. Например, стены здания или плиты, из которых они сложены, имеют одинаковый цвет.

Алгоритм Вариока работает в картинном пространстве. Объекты сцены представлены совокупностью многоугольных граней. Нелицевые грани предварительно удалены. Многогранники отсортированы по глубине объектов.

Рассмотрим окно в картинной плоскости. В простейшем случае это прямоугольник.

Возможны следующие случаи.

1. Окно пусто. Т.е. проекции всех многоугольников лежат вне окна.

2. Окно закрашивается цветом фона.

3. Окно охватывается проекцией некоторого многоугольника, а проекции более близких многоугольников с окном не пересекаются.

4. Окно закрашивается цветом охватывающего многоугольника.

5. Размеры окна не превышают размера пиксела.

6. Принимается специальное решение о закраске. Например, цветом одной из поверхностей, проекция которой попадает в это окно.

7. Ни одно из условий 1 -3 не выполняется.

Окно разбивается на четыре равных подокна и анализируется каждое из подокон.

Процесс разбиения окна на подокна порождает структуру данных, представляющую собой тетрарное дерево, каждый узел которого содержит координаты окна и если это терминальный узел (мест), то цвет окна, иначе - указатели на подокна.