Дешифраторы и шифраторы. Шифратор, (называемый так же кодером) - устройство, осуществляющее преобразование

Рисунок 1

Шифратор, (называемый так же кодером) - устройство, осуществляющее преобразование десятичных чисел в двоичную систему счисления. Пусть в шифраторе имеется m входов, последовательно пронумерованных десятичными числами (0, 1, 2, 3, ..., m - 1), и n выходов. Подача сигнала на один из входов приводит к появлению на выходах n-разрядного двоичного числа, соответствующего номеру возбужденного входа.

Очевидно, трудно строить шифраторы с очень большим числом входов m, поэтому они используются для преобразования в двоичную систему счисления относительно небольших десятичных чисел. Шифраторы широко используются в разнообразных устройствах ввода информации в цифровые системы. Такие устройства могут снабжаться клавиатурой, каждая клавиша которой связана с определенным входом шифратора. При нажатии выбранной клавиши подается сигнал на определенный вход шифратора, и на его выходе возникает двоичное число, соответствующее выгравированному на клавише символу.

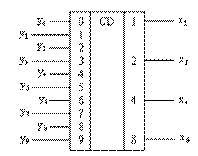
На рис. 1 приведено символическое изображение шифратора, преобразующего десятичные числа 0, 1, 2, ..., 9 в двоичное представление в коде 8421. Символ CD образован из букв, входящих в английское слово CODER. Слева показано 10 входов, обозначенных десятичными цифрами 0, 1, ..., 9. Справа показаны выходы шифратора: цифрами 1, 2, 4, 8 обозначены весовые коэффициенты двоичных разрядов, соответствующих отдельным выходам.

Таблица 1
Десятичное число	Двоичный код 8421
x8	x4	x2	x1

Из приведенного в табл. 1 соответствия десятичного и двоичного кодов следует, что переменная x1 на выходной шине 1 имеет уровень лог. 1, если имеет этот уровень одна из входных переменных y1, у3, у5, у7, у9. Следовательно, x1 = yl \/ y3 \/ y5 \/ y7 \/ y9.

Для остальных выходов x2 = y2 \/ y3 \/ y6 \/ y7; x4 = y4 \/ y5 \/ y6 \/ y7; x8 = y8 \/ y9.

Рисунок 2

Для обратного преобразования двоичных чисел в небольшие по значению десятичные числа используются дешифраторы (называемые также декодерами). Входы дешифратора предназначаются для подачи двоичных чисел, выходы последовательно нумеруются десятичными числами. При подаче на входы двоичного числа появляется сигнал на определенном выходе, номер которого соответствует входному числу.

Дешифраторы имеют широкое применение. В частности, они используются в устройствах, печатающих на бумаге выводимые из цифрового устройства числа или текст. В таких устройствах двоичное число, поступая на вход дешифратора, вызывает появление сигнала на определенном его выходе. С помощью этого сигнала производится печать символа, соответствующего входному двоичному числу.

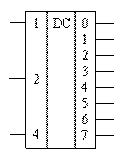
Задание: (Рис 2) Построить символическое изображение дешифратора, символ DС образован из букв английского слова DECODER. Слева показаны входы, на которых отмечены весовые коэффициенты двоичного кода. Справа - выходы, пронумерованные десятичными числами, соответствующими отдельным комбинациям входного двоичного кода. На каждом выходе образуется уровень лог. 1 при строго определенной комбинации входного кода.

По способу построения различают линейные и прямоугольные дешифраторы.

Линейный дешифратор. Рассмотрим построение дешифратора, осуществляющего преобразование, заданное табл. 2

Таблица 2
Входной код 8421	Номер выхода
x8	x4	x2	x1

Значения выходных переменных определяются следующими логическими выражениями:

В линейном дешифраторе выходные переменные формируются по (1)

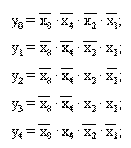(1)

Прямоугольный дешифратор. Рассмотрим принцип построения прямоугольного дешифратора на примере дешифратора с 4 входами и 16 выходами.

Разобьем входные переменные x8, x4, x2, x1 на две группы по две переменные в каждой: x8, x4, и x2, x1. Каждую пару переменных используем в качестве входных переменных отдельного линейного дешифратора на четыре выхода. Выходные переменные линейных дешифраторов определяются логическими выражениями (2):

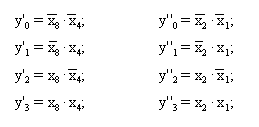(2)

(3)

Эти дешифраторы выполняют функции первой ступени дешифратора.

Выходные переменные y0, y1, ..., y15 прямоугольного дешифратора можно представить логическими выражениями (3), используя в них в качестве аргументов выходные переменные y'0, ..., y'3 и y''0, ..., y''3 линейных дешифраторов.