Доказательство оптимальности кода

Докажем, что код Шеннона-Фано является оптимальным кодом.

1. Код Шеннона-Фано - неравномерный код. Чтобы он был оптимальным, необходимо, чтобы средняя длина кодовой комбинации для определенного алфавита, закодированного этим кодом, была меньше длины кодовой комбинации равномерного двоичного кода, которым можно закодировать этот алфавит.

Средняя длина кодовой комбинации для определенного закодированного алфавита вычисляется по формуле:

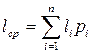, (5)

где l_i – длина кодовой комбинации i-го закодированного символа первичного алфавита,

p_i – вероятность появления i-го символа алфавита.

Эта величина показывает, сколько символов вторичного алфавита (ансамбля сообщений B) приходится на символ первичного алфавита (ансамбля сообщений A) в закодированном сообщении.

По формуле (5) найдем среднюю длину кодовой комбинации для нашего алфавита (количество символов алфавита n = 16), закодированного кодом Шеннона-Фано, и получим следующее значение:

,

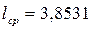то есть в среднем на один символ нашего алфавита приходится 3,8531 двоичных символов.

Количество символов нашего алфавита n = 16. Следовательно, длина кодовой комбинации равномерного двоичного кода, которым можно закодировать наш алфавит, будет равняться 4, поскольку таким кодом можно закодировать алфавит, максимальное количество символов которого будет равняться 2⁴ = 16.

Это означает, что необходимая длина кодовой комбинации равномерного двоичного кода больше средней длины кодовой комбинации Шеннона-Фано.

2. Сравним энтропию источника первичного ансамбля сообщений A (нашего алфавита) с энтропией этого же источника при кодировании его ансамбля сообщений кодом Шеннона-Фано.

Рассчитанная ранее по формуле (3) энтропия источника первичного ансамбля сообщений A равна:

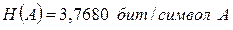
Энтропия этого источника при кодировании его первичного ансамбля сообщений A определенным кодом рассчитывается по формуле:

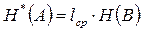, (6)

где l_ср – средняя длина кодовой комбинации закодированного ансамбля сообщений (см. формулу (5)),

H(B) – энтропия источника вторичного ансамбля сообщений B.

Рассчитаем энтропию источника сообщений вторичного алфавита B - H(B). Для этого необходимо найти вероятность появления символов этого алфавита. Положим, что длина текста

.

Для данного текста, закодированного кодом Шеннона-Фано, найдем вероятность появления в нем двоичных символов “0” и “1” – элементов вторичного ансамбля сообщений B. Для этого необходимо подсчитать количество “0” и “1” в закодированном тексте.

Таблица 3

Подсчет количества “0” и “1” в закодированном тексте (исходный текст длиной L = 10 000 символов)

Символ первичного алфавита	Вероятность появления символа первичного алфавита	Закодированный кодом Шеннона-Фано символ	Количество символов в кодовой комбинации	Количество символов в тексте
о	0,1067
а	0,1067
и	0,0933
в	0,0933
к	0,08
н	0,08
с	0,08
е	0,08
л	0,0667
я	0,0667
ч	0,0533
й	0,0267
т	0,0267
ь	0,0133
р	0,0133
г	0,0133
Количество каждого из двоичных символов в закодированном тексте
Длина закодированного текста	38 531

Зная количество “0” и “1” в тексте, а также длину текста, подсчитаем вероятность появления двоичных символов в закодированном тексте:

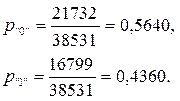
По формуле (3) рассчитаем энтропию источника вторичного ансамбля сообщений B - H(B) (количество символов алфавита n = 2):

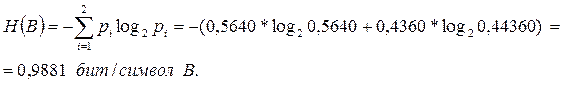
Теперь по формуле (6) найдем энтропию источника при кодировании его первичного ансамбля сообщений A кодом Шеннона-Фано:

.

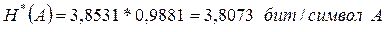Энтропия источника первичного ансамбля сообщений A:

.

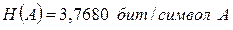Следовательно:

≈ .

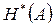Вывод: из двух пунктов доказательства следует, что код Шеннона-Фано является оптимальным.

Код Хаффмана