Выделение системы. Относительно обособленная система

Как же осуществляется выделение или задание некоторого множества элементов в качестве системы? Всегда ли мы можем строго и однозначно говорить об этом?

Обсуждение данного вопроса потребует ввести понятие среды как некоторого дополнения множества «система» (до какого множества - зависит от конкретной постановки задачи). Кроме того, будем считать, что связи между элементами системы являются направленными по линии воздействия одного элемента на другой. Естественным эквивалентом такого представления системы является ориентировочный граф, в котором элементы представлены вершинами, а связи между ними - дугами (рис.1а). Воздействующий элемент будем считать предшествующим, и начало стрелки связи, идущей от него (начало дуги) - выходом этого элемента. Испытывающий воздействие элемент будем считать последующим, и конец стрелки связи, поступающей в него (конец дуги) - входом этого элемента. Частными случаями являются: взаимодействие двух элементов (c и d на рис.1а), когда соединяющиеся две смежные вершины дуги образуют контур, и самосопряжение элемента, когда его выход возвращается на вход, т.е. образуется петля (bна рис.1а).

Введено понятие относительнообособленной (или относительно изолированной) системы, которая связана со средой, по крайней мере, одним входом и одним выходом (2). Собственно можно полагать, что абсолютно обособленная (изолированная или замкнутая) система таких «внешних» входов и выходов не имеет.

Система называется замкнутой тогда т только тогда, если для любого ее элемента существует эффективный процесс идентификации, отнесения к данной системе. В этом случае система не имеет внешних связей, ее элементы взаимодействуют лишь внутри системы. Для незамкнутой системы такая однозначная идентификация невозможна. Здесь элементы, имеющие внешние связи, могут быть отнесены либо к системе, либо к среде, т.е. к другой системе: вершина dна рис.1б стала входом Х₂ и выходом У₂ на рис.1в.

В реальной действительности нет абсолютно обособленных систем. Но зачастую удобно пользоваться этой абстракцией, обрывая на каком-то шаге внешние связи.

Доказана теорема о разложении любой системы n-го порядка на подсистемы. Отсюда вытекает возможность и общность выделения относительно обособленной системы из сколь угодно большой системы.

Вместе с тем выделение системы представляет весьма трудную проблему.

Перечисление связей между переменными (элементами) системы практически неприменимо: ведь даже для системы из ста элементов число комбинаций связей может достичь фантастической цифры 2¹⁰⁰, т.е. порядка 10³³. А какие связи учитывать и какие отбросить - без предварительного исследования сказать нельзя. Перечисление самих переменных также не может быть исходным способом выделения системы. Каждая переменная должна быть задана множеством своих рассматриваемых значений (или векторов значений), что требует предварительного анализа системы, взаимодействия ее переменных друг с другом и со средой.

Поэтому У.Р.Эшби, С.Вир и другие авторы предлагают процедуры операционного характера, позволяющие выделить системы в самом процессе исследования некоторого множества переменных.

Сначала исследователь строит предположение о типе связей межу переменными. Оно может быть осно­вано на некотором опыте или предварительных наблюдениях, а может представлять собой априорную ги­потезу. В любом случае здесь имеет место известное предварительное обобщение, существенно зависящее от постановки задачи, для которой выделяется система.

Тип связей может быть задан в виде некоторого признака - набора присущих или приписываемых пере­менным свойств.

Для формулировки признака необходимо знать шкалу, в которойэтот признак будет оцениваться (измеряться).

Обычно выделяют три вида шкал: номинальные, порядковые и количественные,

Номинальные шкалы позволяют опознавать, раз­личать, идентифицировать объект.

Они исходят из аксиом идентификации:

1. A либо есть В, либо не есть В;

2. если А есть В, то В есть А;

3. если А есть В и В есть С, то А есть С.

Номинальную шкалу называют такие классификационной шкалой. Действительно, здесь каждому объекту при­сваивается определённый ярлык, который свидетельст­вует об отнесении данного объекта к некоторому классу, обозначенному этим ярлыком.

Порядковые шкалы позволяют установить порядко­вое соотношение между объектами по какому-то приз­наку, определить их равноценность или доминирова­ние в этом смысле, но не дают возможности сказать, насколько один объект лучше, важнее и т.п. другого. Помимо аксиом I - З, здесь предполагаются аксиомы упорядочения:

4. если А предшествует (или равноценно) В, то В не предшествует А; либо А пред­шествует (или равноценно В, либо В предшествует (или равноценно) А);

5. если А предшествует (или равноценно) В и В предшествует (или равноценно) С, то А предшествует (или равноценно) С. Аксиома 5 называется аксиомой транзитивности. Исключение из ак­сиом 4 и 5 допущений о равноценности или равно­значности приводит к порядку строгого доминирования.

Количественные шкалы позволяют установить количественное соотношение между объектами. В этом случае признак содержит и единицу измерения. Помимо аксиом I - 5, здесь предполагаются аксиомы аддитивности:

6. если А=Р и В=0, то А+В=Р;

7. А+В=В+А;

8. если А=Р и В=К, to A+В=P+K;

9. от конкретной шкалы признака, а также от характера переменных и зависимостей между ними (детерминированные или вероятностные, линейные или нелинейные).

Эти пороговые значения устанавливаются либо исследователем, либо возможностями наблюдения. Иног­да в неявном виде они вытекают из самого способа задания признака. Но в любом случае требования определения пороговых значений признака переменных системы является необходимым при операционном опреде­лении системы.

3. Общие характеристики системы:

Важнейшими аспектами исследования системы является определение её структурных и функциональных характеристик.

а) Структура системы.

Под структурой системы понимают совокупность связей между ее элементами. Определение структуры системы можно свести к построению соответствующего ориентированного графа.

Число возможных связей между элементами рас­тёт очень быстро с увеличением числа элементов. В системе из n элементов число направленных связей может составить n(n-1), а число комбинаций свя­зей - достигать величины 2ⁿ, для системы из деся­ти элементов максимальное число связей составит 90, а число их комбинаций - 1024,

Большая система характеризуется числом её элементов, и особенно связей. Однако нет какой-либо четко установленной единой пороговой величины, с которой начинается большая система, - эта величина зависит от возможностей исследователя и определя­ется им. Сложная система характеризуется (А+В)+С=А+(В+С). Часто среди количественных шкал выделяют еще интервальные и пропорциональные шкалы.

Интервальные шкалы позволяют измерить расстояние между объектами, сказать, насколько один объект больше другого в принятой единице измерения. Заме­на одной интервальной шкалы на другую допустима в размах линейного преобразования (У=АХ+В).

Пропорциональные шкалы позволяют определить, во сколько раз один объект больше другого. Здесь подразумевается, в отличие от интервальной шкалы, фиксированная, нулевая точка отсчета и, следова­тельно, допускается лишь пропорциональное преобра­зование (У=АХ) этой шкалы.

Скажем, токарь Иванов имеет 5-й тарифный разряд и выработал за смену 30 деталей. Отнесение Иванова к классу токарей производится по номиналь­ной шкале профессий. Присвоение токарю Иванову 5-го разряда осуществляется во порядковой шкале классификации. Измерение сменной выработки токаря Иванова предполагает наличие интервальной шкалы рабочего времени. Определение выработки в деталях производится по пропорциональной шкале.

Множество признаков, которыми могут быть оха­рактеризованы любые реальные объекты, выражают множество реально существующих свойств этих объек­тов и, соответственно, типов связи между ними. Сле­довательно, каждому объекту присущи переменные са­мого различного вида, и в зависимости от того, ка­кие свойства, "стороны" этого объекта принимаются во внимание, он монет быть включён в ту или иную систему.

Выделение определенного типа связей, фиксируемого в признаке, еще не позволяет определить конк­ретную систему. Необходимо ещё установить некоторые граничные (пороговые) значения выраженных в призна­ке свойств переменных. Определение этих пороговых значений свойств существенно зависит многообразием, неоднородностью элементов и (или) связей. Понимание неоднородности также зависит от иссле­дователя, от свойств объектов, которые он рассматривает в рамках данной системы.

Следовательно, может быть большая, но несложная (простая) система - например, Великая китайская стена, воздвигнутая из многих миллионов однородных элементов. Как правило, рост системы ведёт к диффе­ренциации ее элементов и тем самым к усложнению сис­темы. Например, развитие народного хозяйства вызыва­ет переход от однородных натуральных хозяйств к спе­циализированному производству и общественному разделению труда. Соответственно не только увеличивается число связей между хозяйственными единицами, каждая связь становится не только более интенсивной, но и специализированной; возрастает многообразие взаимодействий между элементами: это - экономические, социально-политические, административные и другие отношения людей, технологические операции, потоки материальных благ и денег, обработка данных и т.д. Описать всё это многообразие связей в сложной народнохозяйственной системе на одном языке не удаётся.

Число связей, их направление и разветвленность являются структурными характеристиками системы. Слож­ность выражает уже связь структуры системы с ее содержательным анализом, в котором только и может быть определена неоднородность этой структуры. Обобщенное представление о содержательной стороне анализа системы даёт понятие её функции.

б) Функция системы

Под функцией системы можно понимать характе­ристику, определяющую изменение состояний системы. Но такая характеристика зачастую оказывается очень громоздкой. Для любой относительно обособленной системы практически главным является состояние её выходов, а в случае "черного ящика" мы вообще можем наблюдать и определить лишь изменение состояний его выходов при изменении состояний его входов. Речь идет о наблюдаемых результатах действия системы или о ее поведении. Целью системы называют определённое, "желаемое" (заданное извне или установленное самой системой) состояние её выходов, т.е. некоторое зна­чение или собственное подмножество значений функции системы. В связи с этим саму функцию систему, определяющую состояния выходов, можно называть целевой функцией системы, в отличие от функций системы, ко­торая определяет изменение состояний системы в целом.

Желая более полно выразить связанность, взаимо­зависимость элементов системы говорят о свойстве целостности системы. Констатации числа связей, их направления и многообразия для этого недостаточно. Понятие целостности основывается на предположении, что система представляет собой нечто "большее", а иногда и качественно отличное, чем сумма составляющих её частей. Система обладает новыми свойствами, которых нет у её элементов. Порождение этих свойств и называется эмерджентностью.

Целостность обобщает функциональные характе­ристики системы. Допустимо определить свойство целостности на некоторое правило неаддитивного (точ­нее, супераддитивного) сложения для систем, соглас­но которому функция системы 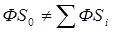"боль­ше" суммы функций, составляющих её элементов: в сложных системах очень часто целевая функция системы вообще не поддастся выражению в терминах элементов этой системы. Особой проблемой является допустимость относить к системам множества связанных объектов с аддитивной функцией (тогда в приведенном выше выражении следует допустить знак равенства).

в) Критерии: функциональный, цели, выживания.

Функциональным критерием будем называть пра­вило, которое каждому состоянию системы приписывает некоторую оценку (возможно, в виде вектора). Пред­полагается одна или несколько шкал оценок. Эти шкалы могут быть количественными, порядковыми или номи­нальными. Функциональный критерий показывает условия, при которых данная система не перестает быть систе­мой, не теряет своей качественной определённости;

это - область ее допустимых состояний.

Критерием цели будет правило, позволяющее оценить поведение или состояние выходов системы. Он позволяет сравнить с целью, т.е. неким "желаемым" состоянием другое, например, фактическое состояние - измерить "расстояние" до цели, выяснить по каждому состоянию, лучше оно или хуже относительно цели, до­пустимо или недопустимо.

Критерий выживания определяет область допусти­мых линий поведения системы, т.е. условия, при которых существенные переменные не выходят за заданные критические пределы. Существенными переменными на­зывают переменные, которые влияют на поведение сис­темы в наблюдаемых или заданных (как правило, огра­ниченных) пределах. Система "выживает" - это зна­чит, что, несмотря на возмущения, сохраняются те свойства (характеристики) в соответствии с которыми данное множество элементов было выделено в ка­честве системы. Таким образом, критерий выживания тесно связан с понятием устойчивости системы.

Кибернетические исследования систем показали высокую эффективность функционального подхода, при котором в первую очередь анализируется функциониро­вание, преобразование, поведение систем и этой це­ли подчинено также изучение структурных характе­ристик.

г) Анализ и синтез системы.

Функциональный и структурный подходы по-разному соотносятся на стадии анализа и стадии синтеза систем.

Анализом системы является определение ее функции на основе известной (или заданной) структуры. Синтезом системы является построение её структуры, реализующей заданную функцию или класс функций.

При анализе и синтезе сложных систем важное значение имеет методологический принцип неопределённости.

В сложных системах может не быть взаимно од­нозначного соответствия между структурой и функцией.

Одна и та же функция может быть в принципе реализована некоторым множеством структур, и, на­оборот, определенная структура может (с какой-то вероятностью) выполнять некоторое множество функций. В лучшем случае можно выделить классы структур и классы функций, и очень редко удаётся установить взаимно однозначное соответствие между классами структур и функций.

Иерархия систем

Наблюдатель выделил систему и исследовал ее характеристики. Но полученные им результаты не абсолют­ны. Переменные (элементы) данной системы, в свою очередь, могут рассматриваться в качестве системы, т.е. каждая данная система может быть разделена на подсистемы, а каждая подсистема - снова разбита на подсистемы более "низкого" уровня. Элементом дан­ной системы будет такая подсистема, в которой не рассматриваются подсистемы низшего уровня.

На подсистемы может быть разбита как простая, так и сложная система. Для простой системы такое разбиение лишь "снизу" условно ограничено выде­ленными элементами этой системы. Разбиение носит структурный характер.

Поскольку сложная система совмещает несколько аспектов рассмотрения, то её разбиение на подсисте­мы связано с этими аспектами.

Сложную систему можно рассматривать как совокупность относительно обособленных взаимосвязанных подсистем, для каждой из которых может бить определена цель функционирования, подчинённая общей цели системы.

Положение о разбиении системы на подсистемы является общим. Поэтому, с другой стороны, данная система сама может рассматриваться в качестве подсистемы или элемента другой, более общей системы (суперсистемы). Соответственно будут переопределены её связи с внешней средой - часть этих связей (или все связи) теперь будут выражать отношения данной системы внутри суперсистемы.

Таким образом, может быть построена иерархия систем. Исследователь выделяет некоторую систему, берёт её в качестве "точки отсчёта" и расширяет рассмотрение "вверх" и "вниз" на одну или несколько ступеней. При переходе "вверх" выделенная система переопределяется в качестве подсистемы некоторой суперсистемы. При движении " вниз" данная система расчленяется на подсистемы. Число и характер рассматриваемых ступеней зависят от выделения некоторого множества переменных в качестве системы и последу­ющего их переопределения при переводе на другую ступень.

Исследователь, например, может рассматривать мировую экономику и её переменными считать народ­нохозяйственные комплексы отдельных стран; при анализе системы народного хозяйства страны можно выде­лить отраслевые или районные комплексы, каждый из которых является системой предприятий. Экономическую систему любого из этих уровней можно делить по многим как структурным, так и функциональным приз­накам.

Система предприятия будет иметь в качестве переменных систему производства, финансовую систему, систему снабжения, сбыта, которые также состоят из некоторых наборов переменных (рабочих мест, счетов, складов и материалов).

В зависимости от того, какой уровень принят, исследователем за исходный, при обратном переходе "вверх" от соответствующего уровня будут получены суперсистемы, т.е. системы более высокого уровня.

При, планировании иерархии моделей общественного производства первостепенное значение приобретает вопрос о степени детализации экономических расчетов. В нашем народном хозяйстве действуют десятки тысяч предприятий, номенклатура производимой и потребляемой продукции насчитывает десятки миллионов наименований. Построить единую модель, отражающую функционирование и взаимосвязи между этим гигантским числом компонентов и в централизованном порядке их рассчитать и сбалансировать, невозможно даже с помощью самых совершенных средств вычислительной техники. Это с неизбежностью обусловливает необходимость многоступенчатой, иерархической организации планирования и управления. В соответствии с этим возникает иерархия моделей планирования и управления.

Применительно к существующей организации хозяйст­венного руководства эта иерархия моделей охватывает три вертикальных уровня иерархии:

1. модели предпри­ятий;

2. отраслевые модели;

3. народнохозяйственная модель, отражающая связи между отраслями.

Комплекс включает также модели планированияобщественного производства в территориальном разрезе. Взаимодейст­вие между элементами и подсистемами общественного производства двояким образом отражается во взаимодействии между их моделями. С одной стороны, входы и выходы моделей различных подсистем охватываются сетью прямых и обратных информационных связей, с другой стороны - общей для всех моделей является первичная информация, возникающая в процессе про­изводства, потребления и распределения материальных ценностей.

В модели предприятия первичная информация, характеризующая его производственно-хозяйственную деятельность за прошлый период технико-экономические нормы, структуру основных фондов, трудовых затрат, является входной. Вместе с внешней вход­ной информацией (плановые задания вышестоящей организации, заказы по договорам, спрос на продук­цию) она служит для выработки показателей плана предприятия, являющихся выходом модели.

Укрупнённые (агрегированные) показатели - планово-экономические и отчетные по предприятиям дан­ные о научно-техническом прогрессе, плановые задания для отрасли, сведения о потребности в продукции отрасли - служат входной информацией отраслевой модели. Выходом модели являются показатели отрас­левого плана и плановые задания предприятиям.

Аналогичным путем на основе отраслевых показа­телей и информации внешней по отношению к системе общественного производства (количество и структура трудоспособного населения, наличие разведанных и освоенных природных запасов сырья и сельскохозяйст­венных угодий, объём наличных материальных ресур­сов, внешнеторговые связи, потребности обороны) формируется входная информация народнохозяйственной модели. Выходом модели являются глобальные показатели развития народного хозяйства (производство и распре­деление национального дохода, фонды личного и общест­венного потребления), a также плановые задания отрас­лям.

От степени детализации показателей планов различных уровней иерархии зависит соотношение между объёмами информации, циркулирующей и обрабатываемой на уровне предприятий и на вышестоящих уровнях планирования, размерность отраслевых и народнохо­зяйственных моделей, метода их реализации.