Расчет маневра расхождения с одним судном

Расчет маневра расхождения заключается в том, чтобы направить линию относительного движения на безопасное расстояние от нашего судна. Поскольку маневр невозможно предпринять мгновенно в момент получения последней точки наблюдения (на основе которой производится оценка ситуации), необходимо принять точку упреждения У - точку, в которой будет встречное судно в момент, когда вы предпримите маневр (рис.6).

Примечание. В принципе, точка У выбирается произвольно, однако, на практике удобнее ее устанавливать через интервал времени, кратный интервалу времени между наблюдениями, т.к. в этом случае достаточно измерителем снять расстояние между точками наблюдения и отложить этот раствор от последней точки на продолжение ЛОД. Поскольку время между наблюдениями обычно принимается 3 мин., то и точка упреждения устанавливается через интервал, кратный 3 мин.

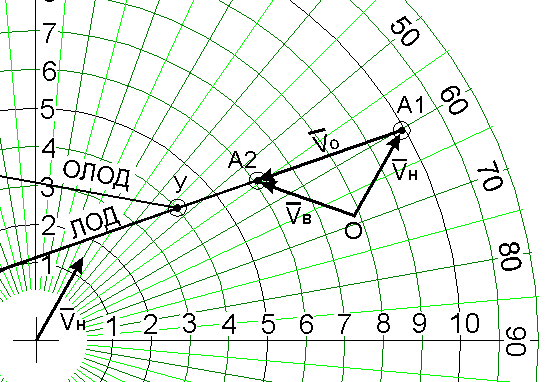
Рис.6.

Мы знаем, что направление ЛОД (ОЛОД) определяется направлением вектора относительной скорости. А вектор относительной скорости мы можем изменить лишь изменив вектор собственной скорости (рис.7).

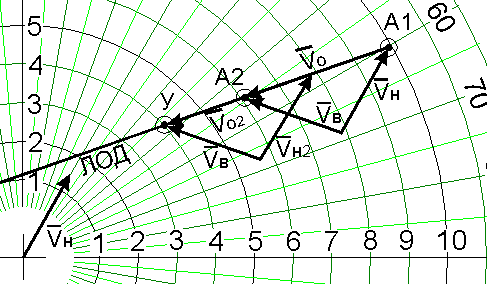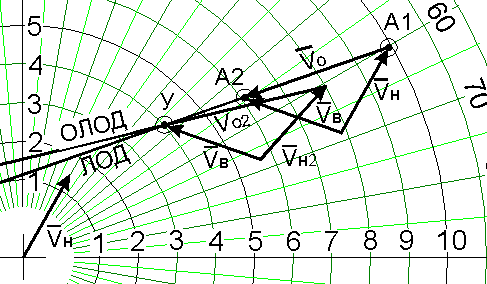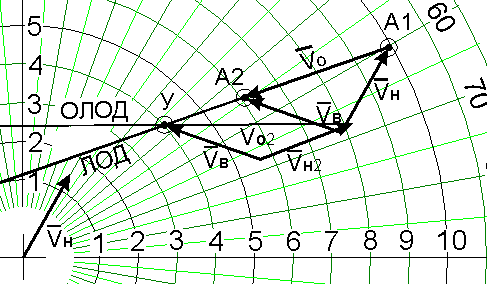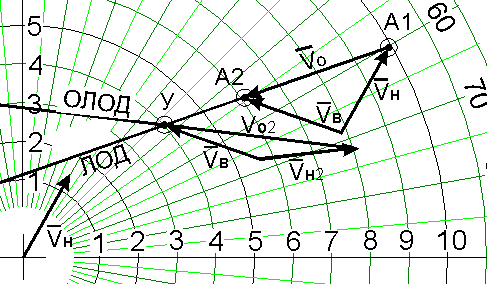
Рис.7.

Предположим, что мы решили разойтись на дистанции 3 мили. Это значит, что ЛОД должна пройти по касательной к окружности, соответствующей 3-мильной дистанции. Проведя из точки У касательную к 3-мильной дистанции мы получим ОЛОД - ожидаемую линию относительного движения.

Но для получения необходимой ОЛОД нужно так изменить векторный треугольник, чтобы новый вектор V_о лежал на ОЛОД. Этого можно было бы добиться, построив новый векторный треугольник при точке У (рис.8)

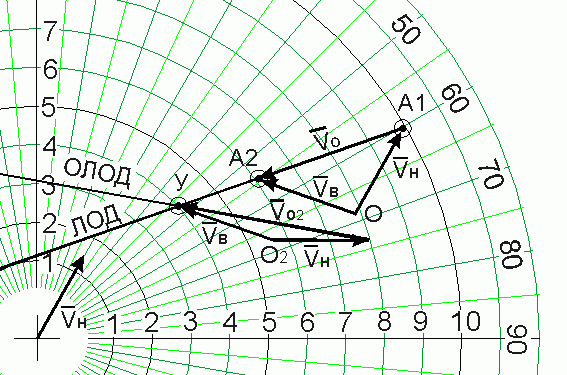
Рис.8.

Действия:

1. переносим в т.У вектор скорости встречного судна V_в без изменения (поскольку оно не маневрирует)

2. продляем ОЛОД вправо от т. У для построения вектора V_о2

3. из начала вектора V_в (точка О2) откладывает вектор нашей скорости V_н в таком направлении, чтобы его конец ложился на ОЛОД

Полученное таким образом новое направление вектора скорости нашего судна и есть искомый курс расхождения на заданной дистанции.

Важно обратить внимание на соответствие длины вектора V_н , "воткнутого" в т.А1, интервалу времени между первой и последней точками встречного судна. Если этот интервал времени составляет 6 мин., то и длина вектора V_н должна соответствовать расстоянию, проходимому за 6 мин. Если этот интервал времени составляет, например, 9 или 12 мин., то и длина вектора V_н должна соответствовать расстоянию, проходимому за 9 или 12 мин. соответственно. Все векторы "скоростного треугольника" соответствуют одному и тому же временному интервалу.

Рассмотренное на рис.3 построение загромождает планшет и требует выполнения построений, которых можно избежать. Более экономичным по времени решением является следующее (рис.9):

1. ОЛОД параллельно переносится в т.А2

2. вектор V_н поворачивается относительно т.О таким образом, чтобы лечь острием на линию, параллельную ОЛОД

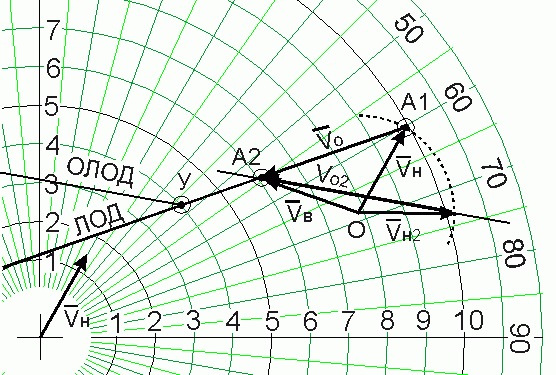
Рис.9.

! Вектор V_{н 2} - это вектор, показывающий курс и скорость, которые должно иметь наше судно после маневра чтобы разойтись со встречным судном на дистанции 3 мили, если маневр будет совершен в данной точке упреждения т.У.

Следует обратить внимание на то, что рассмотренный пример предусматривает маневр только путем изменения курса нашего судна. Если бы задача решалась только с точки зрения геометрии, то мы бы имели целый сектор возможных сочетаний курсов и скоростей, которые бы удовлетворяли поставленной задаче (ри.10).

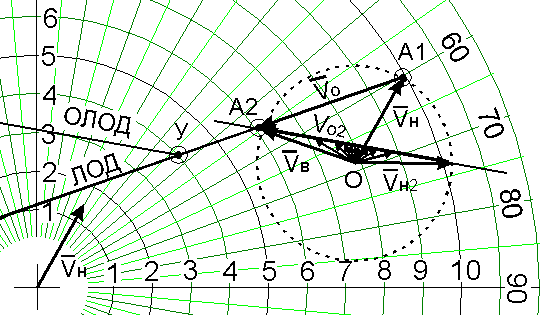
Рис.10.

Из рисунка видно, что любой вектор V_н , опирающийся острием на снесенную ОЛОД, задает нужное направление вектора относительной скорости (меняется только величина V_о2):

· изменение вектора V_н только по направлению соответствует маневру изменением только курса;

· изменение вектора V_н только по величине соответствует маневру изменением только скорости;

· изменение вектора V_н по величине и направлению соответствует маневру изменением курса и скорости.

На рис.10 рассмотрен только сектор возможных сочетаний курсов и скоростей, которые направят встречное судно точно по ОЛОД. Но обычно ставится задача не точного расхождения на заданной дистанции, а расхождение на дистанции не ближе заданной. Посмотрим, как будет проходить ОЛОД при различных курсах нашего судна (рис.11).

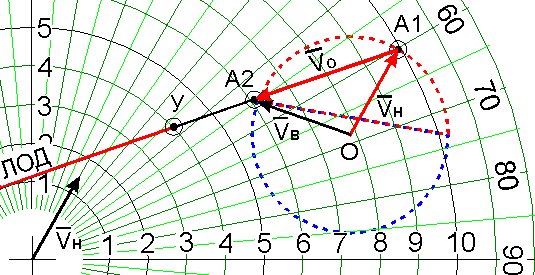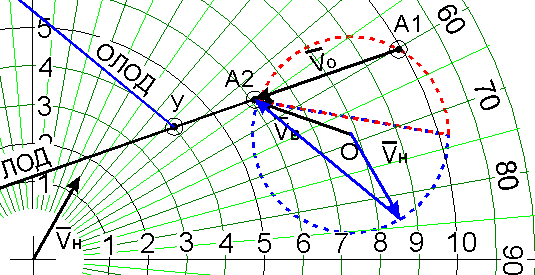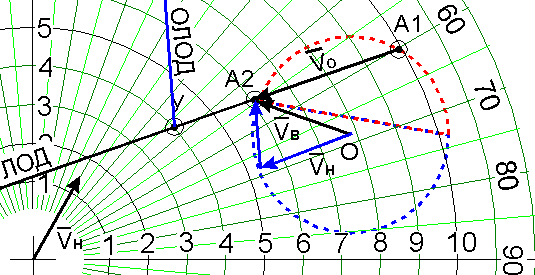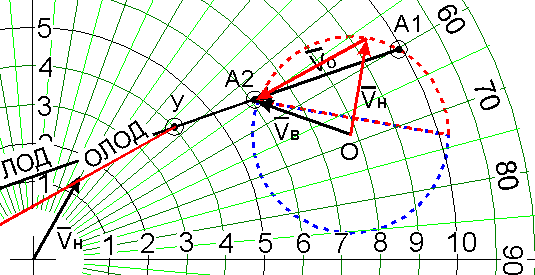
Рис.11.

На основании вышеизложенного можно утверждать, что любое сочетание курса и скорости нашего судна обеспечит расхождение на дистанции, не ближе заданной, если вектор V_н будет находиться в пределах заштрихованного сектора (рис.12).

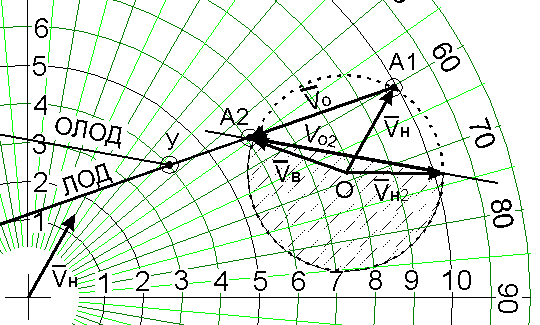
Рис.12.

Это был рассмотрен вариант, когда мы планируем расходиться со встречным судном левым бортом. Если делать сразу предварительную оценку возможности расхождения и правым бортом, то на планшете необходимо провести точно такие же построения и справа од нашего судна:

· провести ОЛОД справа;

· снести ОЛОД в точку А2;

· определить сектор возможных сочетаний курса и скорости.

Из множества возможных вариантов судоводитель должен выбрать оптимальный, руководствуясь рядом условий:

· соблюдение правил МППСС;

· наличие других судов;

· наличие навигационных опасностей;

· особенности своего судна;

· другие обстоятельства, могущие повлиять на безопасность маневра.

В общем случае маневр курсом предпочтительнее маневра скоростью. Дело в том, что на изменение скорости требуется больше времени, чем на изменение курса, и кроме того, потеря скорости превращает судно в пассивного наблюдателя за развитием ситуации. И если ситуация начнет развиваться в опасную сторону, то потерявшее скорость судно будет уже не в состоянии предотвратить столкновения поскольку на разгон судна уходит существенно больше времени, чем на торможение. Только для относительно небольших судов нет разницы как маневрировать при расхождении - курсом или скоростью.

И еще одно замечание. Обычно, при расчете маневра курсом просто поворачивают вектор своей скорости, как было рассмотрено в примере (рис.8). Правила МППСС требуют при расхождении избегать небольших изменений курса, чтобы другое судно могло однозначно понимать ваш маневр. Исходя из этого обычно рекомендуется в подобных случаях изменять курс не менее чем на 30^о. Однако, выход судна на циркуляцию всегда приводит к падению скорости (так при повороте на контркурс падение скорости может достигать 50% от первоначальной скорости). Это не всегда может иметь существенное значение, но помнить об этом следует.