Упакованные целые числа
В АСК современных микропроцессоров имеются команды, оперирующие целыми числами, представленными в упакованном виде. Связано это с обработкой мультимедийной информации. Упаковка предполагает объединение в пределах достаточно длинного слова нескольких целых чисел меньшей разрядности, а соответствующие команды обрабатывают все эти числа параллельно. Такие команды появились в рамках технологии ММХ (MultiMedia extension) фирмы Intel и похожей технологии 3DNow! фирмы AMD. Со временем сформировалась единая технология, известная под аббревиатурой SSE (Streaming SIMD Extensions). В микропроцессорах последних поколений — это версия SSE4, но уже ведется разработка варианта SSE5. В SSE4 за основу принято 128-разрядное слово и предусмотрены четыре формата упакованных целых чисел (рис. 14).
Байты в формате упакованных байтов нумеруются от 0 до 15, причем байт 0 располагается в младших разрядах 128-разрядного слова. Аналогичная система нумерации и размещения упакованных чисел применяется для 16-разрядных (номера 0-7), 32-разрядных (номера 0-3) и 64-разрядных (номера 0-1) целых чисел.
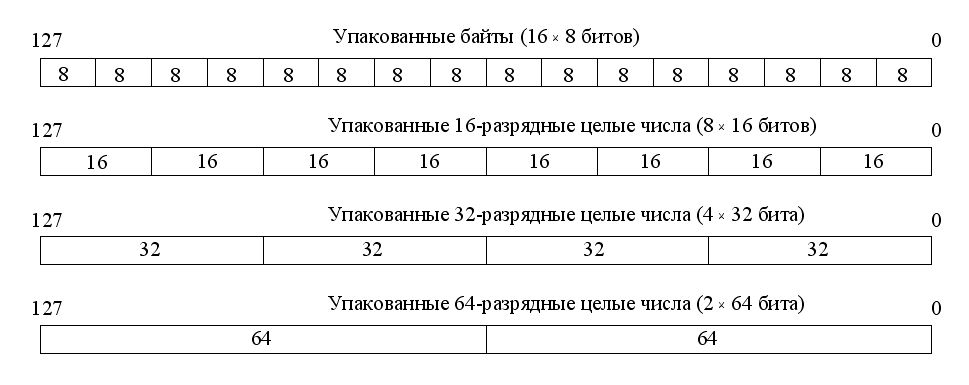
Рис. 14. Форматы упакованных целых чисел в технологии SSE4
Десятичные числа
В ряде задач, главным образом, учетно-статистического характера, приходится иметь дело с хранением, обработкой и пересылкой десятичной информации. Особенность таких задач состоит в том, что обрабатываемые числа могут состоять из различного и весьма большого количества десятичных цифр. Традиционные методы обработки с переводом исходных данных в двоичную систему счисления и обратным преобразованием результата зачастую сопряжены с существенными накладными расходами. По этой причине в ВМ применяются иные специальные формы представления десятичных данных. В их основу положен принцип кодирования каждой десятичной цифры эквивалентным двоичным числом из четырех битов (тетрадой), то есть так называемым двоично-десятичным колом (BCD — Binary Coded Decimal). Обычно используется стандартная кодировка 8421, где цифры в обозначении кодировки означают веса разрядов. Десятичные цифры 0, 1,2, 3, 4, 5, 6, 7, 8,9 кодируются двоичными комбинациями 0000,0001,0010,0011,0100,0101,0110,0111,1000,1001 соответственно. Оставшиеся шесть комбинаций (1010,1011,1100, 1101,1110,1111) используются для представления знаков «+» и «-», а также возможных служебных символов. Знак «+» принято обозначать как 1100 (С16), а знак «-» — как 1101 (D16). Такое соглашение принято исходя из того, что обозначение соответствующих шестнадцатеричных цифр можно рассматривать как аббревиатуру бухгалтерских терминов «кредит» (Credit) и «дебет» (Debit), а именно в бухгалтерских расчетах чаще всего используется рассматриваемая форма представления информации. Другие допустимые обозначения знаков — это 1010 (А16) или 1110 (Е16) для «+» и 1011 (В16) для «-». Иногда допускается представление десятичных чисел без знака, и тогда в позиции, отводимой под знак, записывается комбинация1111 ( F16).
В вычислительных машинах нашли применение два формата представления десятичных чисел (все числа рассматриваются как целые): упакованный и зонный. В обоих форматах каждая десятичная цифра представляется двоичной тетрадой, то есть заменяется двоично-десятичным кодом.

Рис.15 Форматы десятичных чисел: а – упакованный; б - зонный
Наиболее распространен упакованный формат (рис. 15, а), позволяющий не только хранить лесятичные числа, но и производить над ними арифметические операции. В данном формате запись числа имеет вид цепочки байтов, где каждый байт содержит коды двух десятичных цифр. Правая тетрада младшего байта предназначается для записи знака числа. Десятичное число должно занимать целое количество байтов. Если это условие не выполняется, то четыре старших двоичных разряда левого байта заполняются нулями. Так, представление числа -7396 в упакованном формате имеет вид, приведенный на рис 16.

Рис. 16. Представление числа -7396 в упакованном формате
Зонный формат (рис. 15, б) распространен, главным образом, в больших универсальных ВМ. В нем под каждую цифру выделяется один байт, где младшие четыре разряда отводятся под код цифры, а в старшую тетраду (поле зоны) записывается специальный код «зона», не совпадающий с кодами цифр и знаков. В ЭBM это код 11112 — FI6. Исключение составляет байт, содержащий младшую цифру десятичного числа, где в поле зоны хранится знак числа. 11а рис. 17 показана запись числа -7396 в зонном формате. В некоторых ВМ принят вариант зонного формата, где поле зоны заполняется нулями.

Рис. 17 Представление числа -7396 в зонном формате
Размещение знака в младшем байте, как в зонном, так и в упакованном представлениях, позволяет задавать десятичные числа произвольной длины и передавать их в виде цепочки байтов. В этом случае знак указывает, что байт, в котором он содержится, является последним байтом данного числа, а следующий байт последовательности — это старший байт очередного числа.
Рассмотренный вариант двоично-кодированного представления десятичных цифр с весами 8421 наиболее распространен, но не является единственным. Возможные иные схемы кодирования приведены в табл.:
Варианты двоично-кодированного представления десятичных цифр
| Цифра | BCD 8 4 2 1 | Excess-3(код Стибица) | BCD 2 4 2 1 | BCD 8 4 -2 -1 | BCD 8 4 2 1 (IBM 702, 705) |
Использование 4-х двоичных цифр для представления одной десятичной цифры по своей сути избыточно. В то же время при иной системе кодирования для представления десятичного числа из трех цифр достаточно 10 двоичных разрядов. Два наиболее известных варианта такого «экономичного» кодирования — код Чен- Хо (Tien Chi Chen, Irving Т. Но) и плотно упакованный десятичный код (DPD — Densely Packed Decimal).
В обоих вариантах каждая десятичная цифра классифицируется по значению старшего бита в ее представлении в коде BCD на «маленькую» 0-7 (00002-01112) или «большую» 8-9 (10002-10012). Для идентификации маленькой цифры (М) достаточно 3 бита, а большой (Б) — одного бита.
При таком представлении возможны следующие комбинации из трех десятичных цифр:
· M + M + M (требуется 9 битов для цифр и остается 1 бит для идентификации этой комбинации);
· M + M + Б, или M + Б + М, или Б + M + M (требуется 7 битов для цифр и остается 3 бита для идентификации этих комбинаций);
· M + Б + Б, или Б + M + Б, или Б + Б + M (требуется 5 битов для цифр и остается 5 битов для идентификации этих комбинаций);
· Б + Б + Б (3 бита для цифр и 7 битов для индикации этой комбинации, хотя нужно только 5).
Для идентификации конкретной комбинации используются те из 10 битов, которые остались свободными после представления закодированных значений цифр. Различие в методах кодирования Чен-Хо и DPD состоит в способе формирования идентификатора комбинации. В табл. 6 приведены примеры кодировки троек десятичных чисел в кодах BCD, Чен-Хо и DPD.
Табл.6 Примеры представления десятичных чисел в разных кодировках
| Десятичное число | BCD 8421 | Чен-Хо | DPD |
| 0000 0000 0101 | 000 000 0101 | 000 000 0101 | |
| 0000 0000 1001 | 110 000 0001 | 000 000 1001 | |
| 0000 0101 0101 | 000 010 1101 | 000 101 0101 | |
| 0000 0111 1001 | 110 011 1001 | 000 111 1001 | |
| 0000 1000 0000 | 101 000 0000 | 000 000 1010 | |
| 0000 1001 1001 | 111 000 1001 | 000 101 1111 | |
| 0101 0101 0101 | 010 110 1101 | 101 101 0101 | |
| 1001 1001 1001 | 111 111 1001 | 001 111 1111 |
Числа в форме с плавающей запятой
От недостатков ФЗ в значительной степени свободна форма представления чисел с плавающей запятой (ПЗ), известная также под названиями нормальной или полулогарифмической формы. В данном варианте каждое число разбивается на две группы цифр. Первая группа цифр называется мантиссой, вторая — порядком. Число представляется в виде произведения
X = ±mq±p ,
где т — мантисса числа Х, р — порядок числа, q — основание системы счисления.
Для представления числа в форме с ПЗ требуется задать знаки мантиссы и порядка, их модули в q-ричном коде, а также основание системы счисления (рис.18). Нормальная форма неоднозначна, так как взаимное изменение m ир приводит к «плаванию» запятой, чем и обусловлено название этой формы.

Рис. 18 Форма представления чисел с плавающей запятой
Диапазон и точность представления чисел с ПЗ зависят от числа разрядов, отводимых под порядок и мантиссу. На рис. 19 показаны диапазоны разрядностей порядка и мантиссы, характерные для известных ВМ.
Помимо разрядности порядка и мантиссы, диапазон представления чисел зависит и от основания используемой системы счисления, которое может быть отличным от 2. Например, в универсальных ВМ (мэйнфреймах) фирмы IBM используется база 16. Это позволяет при одинаковом количестве битов, отведенных под порядок, представлять числа в большем диапазоне. Так, если поле порядка равно 7 битам, максимальное значение qp, на которое умножается мантисса, равно 2128 (при q = 2) или 16128 (при q = 16), а диапазоны представления чисел соответственно составят:
10-19 < |Х| < 10+19 и 10-76 < |Х| < 10+76. Известны также случаи использования базы 8, например, в ВМ В-5500 фирмы Burroughs.
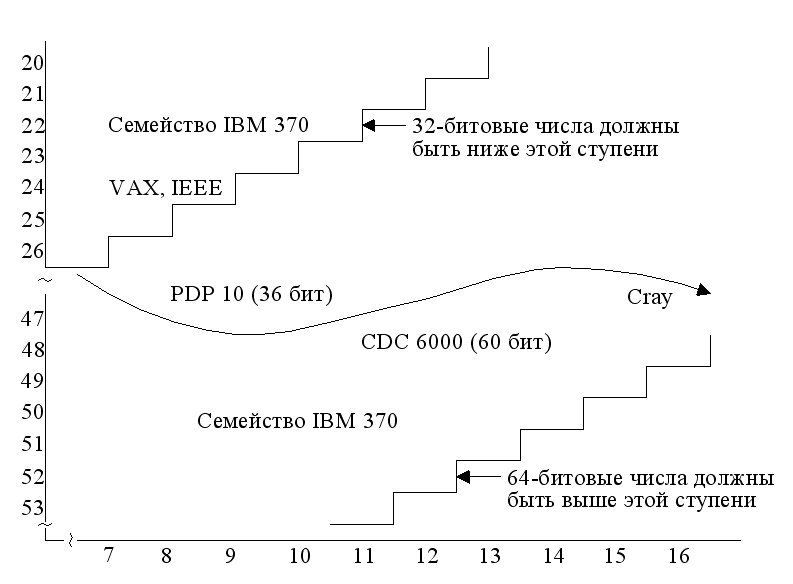
Рис.19 Типовые разрядности полей порядка и мантиссы
В большинстве вычислительных машин для упрощения операций над порядками последние приводят к целым положительным числам, применяя так называемый смещенный порядок. Для этого к истинному порядку добавляется целое положительное число — смещение (рис. 20). Например, в системе со смещением 128, порядок -3 представляется как 125 (-3 + 128). Обычно смещение выбирается равным половине представимого диапазона порядков. Смещенный порядок занимает все биты поля порядка, в том числе и тот, который ранее предназначался для записи знака порядка.

Рис. 20 Формат числа с ПЗ со смещенным порядком
Мантисса в числах с ПЗ обычно представляется в нормализованной форме. Это означает, что на мантиссу налагаются такие условия, чтобы она по модулю была меньше единицы (|q|< 1), а первая цифра после запятой отличалась от нуля. Полученная таким образом мантисса называется нормализованной. Для применяемых в ВМ систем счисления можно записать:
· двоичная: X = т∙2p, (1 > |т| ≥ 1/2);
· восьмеричная: Х=m∙8р, (1 > |т| ≥ 1/8)
· шестнадцатеричная: Х=m∙16p, (1 > |т| ≥ 1/16)
Если первые i цифры мантиссы равны нулю, для нормализации ее нужно сдвинуть относительно запятой на х разрядов влево с одновременным уменьшением порядка на i единиц. В результате такой операции число не изменяется:
| База | До нормализации | После нормализации | ||
| Порядок | Мантисса | Порядок | Мантисса | |
| 0,000110 | 0,110000 | |||
| 0,001010 | 0,101000 |
В примере для шестнадцатеричной системы после нормализации старшая цифра в двоичном представлении содержит впереди три нуля (0001). Это несколько уменьшает точность представления чисел по сравнению с двоичной системой при одинаковом числе двоичных разрядов, отведенных под мантиссу.
Если для записи числа с ПЗ используется база 2 (q = 2), то часто применяют еще один способ повышения точности представления мантиссы, называемый приемом скрытой единицы. Суть его в том, что в нормализованной мантиссе старшая цифра всегда равна единице (для представления нуля используется специальная кодовая комбинация), следовательно, эта цифра может не записываться, а подразумеваться. Запись мантиссы начинают с ее второй цифры, и это позволяет задействовать дополнительный значащий бит для более точного представления числа. Следует отметить, что значение порядка в данном случае не меняется. Скрытая единица перед выполнением арифметических операций восстанавливается, а при записи результата — удаляется. Таким образом, нормализованная мантисса 0,101000(1) при использовании способа «скрытой единицы» будет иметь вид 0,010001 (в скобках указана цифра, не поместившаяся в поле мантиссы при стандартной записи).
Для более существенного увеличения точности вычислений под число отводят несколько машинных слов, например два. Дополнительные биты, как правило, служат для увеличения разрядности мантиссы, однако в ряде случаев часть из них может отводиться и для расширения поля порядка. В процессе вычислений может получаться ненормализованное число. В таком случае ВМ, если это предписано командой, автоматически нормализует его.
Рассмотренные принципы представления чисел с ПЗ поясним на примере [143]. На рис. 2.21 представлен типичный 32-битовый формат числа с ПЗ. Старший (левый) бит содержит знак числа. Значение смещенного порядка хранится в разрядах с 30-го по 23-й и может находиться в диапазоне от 0 до 255.

Рис. 21 Типичный 32-битовый формат числа с плавающей запятой
Для получения фактического значения порядка из содержимого этого поля нужно вычесть фиксированное значение, равное 128. С таким смещением фактические значения порядка могут лежать в диапазоне от -128 до +127. В примере предполагается, что основание системы счисления равно 2. Третье поле слова содержит нормализованную мантиссу со скрытым разрядом (единицей). Благодаря такому приему 23-разрядное поле позволяет хранить 24-разрядную мантиссу в диапазоне от 0,5 до 1,0.
На рис. 22 приведены диапазоны чисел, которые могут быть записаны с помощью 32-разрядного слова.
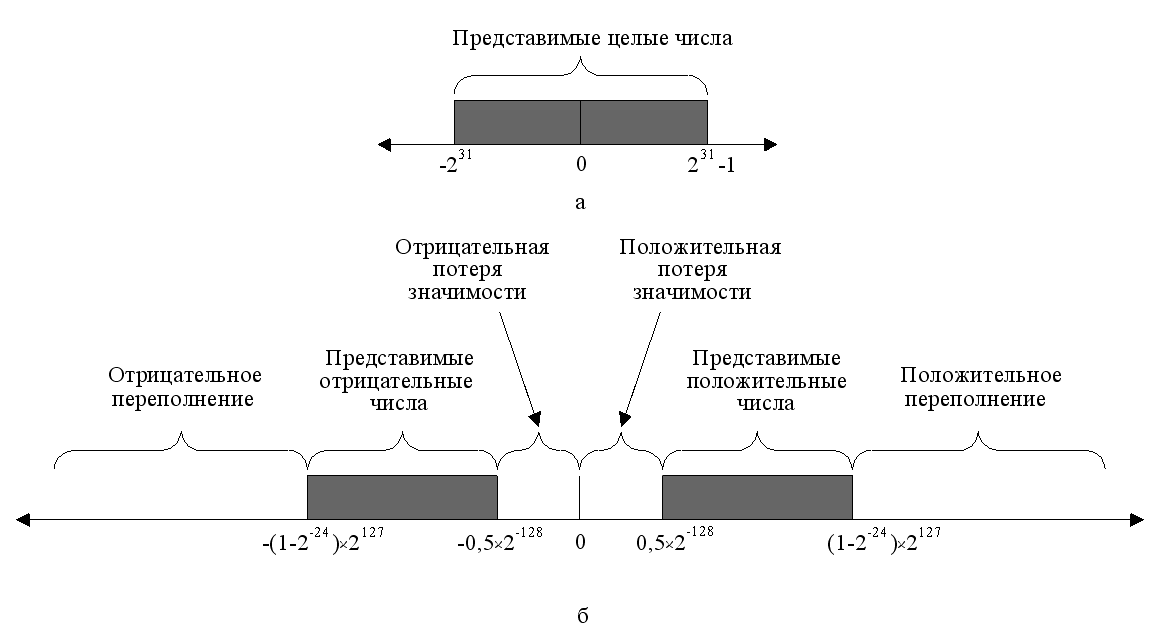
Рис. 22 Числа, представимые в 32-битовых форматах: а - целые числа с фиксированной запятой; б – числа с плавающей запятой.
В варианте с ФЗ для целых чисел в дополнительном коде могут быть представлены все целые числа от -231 до 231 - 1, то есть всего 232 различных чисел (рис. 22, а). Для случая ПЗ возможны следующие диапазоны чисел (рис. 22, б):
· отрицательные числа между -(1 - 2-24)∙2127 и -0,5∙2-128;
· положительные числа между 0,5∙2-128 и (1 - 2-24)∙2127.
в эту область не включены участки:
· отрицательные числа, меньшие чем -(1 - 2-24)∙2127 — отрицательное переполнение;
· отрицательные числа, большие чем -0,5∙2-128 — отрицательная потеря значимости;
· положительные числа, меньшие чем 0,5∙2-128 — положительная потеря значимости;
· положительные числа, большие чем (1 -2-24)∙2127 — положительное переполнение.
Показанная запись числа с ПЗ не учитывает нулевого значения. Для этой цели используется специальная кодовая комбинация. Переполнения возникают, когда в результате арифметической операции получается значение большее, чем можно представить порядком 127 (2120 х 2100 = 2230). Потеря значимости — это когда результат представляет собой слишком маленькое дробное значение (2-120 ∙ 2-100 =2-230). Потеря значимости является менее серьезной проблемой, поскольку такой результат обычно рассматривают как нулевой.
Следует также отметить, что числа в формате ПЗ, в отличие от чисел в форме с ФЗ, размещены на числовой оси неравномерно. Возможные значения в начале числовой оси расположены плотнее, а по мере движения вправо — все реже (рис. 23). Это означает, что многие вычисления приводят к результату, который не является точным, то есть представляет собой округление до ближайшего значения, представимого в данной форме записи.
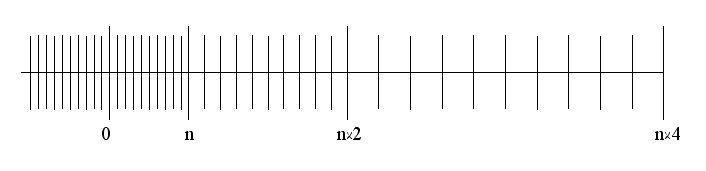
Рис. 23 Плотность чисел с плавающей запятой на числовой оси
Для формата, изображенного на рис 21, имеет место противоречие между диапазоном и точностью. Если увеличить число битов, отведенных под порядок, расширяется диапазон представимых чисел. Однако, поскольку может быть представлено только фиксированное число различных значений, уменьшается плотность и тем самым точность. Единственный путь увеличения как диапазона, так и точности — увеличение количества разрядов, поэтому в большинстве ВМ предлагается использовать числа в одинарном и двойном форматах. Например, число одинарного формата может занимать 32 бита, а двойного — 64 бита.
Числа с плавающей запятой в разных ВМ имеют несколько различных форматов. В табл. 7 приводятся основные параметры для нескольких систем представления чисел в форме с ПЗ. В настоящее время для всех ВМ рекомендован стандарт, разработанный общепризнанным международным центром стандартизации IEEE (Institute of Electrical and Electronics Engineers).
Табл. 7 Варианты форматов чисел с плавающей запятой
| Параметр | IBM 390 | VAX | IEEE 754 |
| Длина слова, бит | О:32; Д: 64 | О:32; Д: 64 | О:32; Д: 64 |
| Порядок, бит | О:8; Д: 11 | ||
| Мантисса,m | О:6 цифр Д: 14 цифр | О: (1) + 23 бита Д: (1) + 55 бита | О: (1) + 23 бита Д: (1) + 52 бита |
| Смещение порядка | О:127; Д: 1023 | ||
| Основание системы счисления | |||
| Скрытая 1 | Нет | Да | Да |
| Запятая | Слева от мантиссы | Слева от скрытой 1 | Справа от старшего бита мантиссы |
| Диапазон мантиссы | (1/16)≤m<1 | (1/2)≤m<1 | 1≤m<1 |
| Представление мантиссы | Величина со знаком | Величина со знаком | Величина со знаком |
| Максимальное положительное число | 1663≡1076 | 2126≡1038 | 21024≡10308 (Д) |
| Точность | О: 16-6≡10-7 Д: 16-14≡10-17 | О: 2-24≡10-7 Д: 2-564≡10-17 | О: 2-23≡10-7 Д: 2-524≡10-16 |
Где О – одинарный формат; Д – двойной формат.
Стандарт IEEE 754
Рекомендуемый для всех ВМ формат представления чисел с плавающей запятой определен стандартом IEEE 754. Этот стандарт был разработан с целью облегчить перенос программ с одного процессора на другие и нашел широкое применение практически во всех процессорах и арифметических сопроцессорах.
Стандарт определяет 32-битовый (одинарный) и 64-битовый (двойной) форматы (рис.24) с 8- и 11-разрядным порядком соответственно. Основанием системы счисления является 2. В дополнение, стандарт предусматривает два расширенных формата, одинарный и двойной, фактический вид которых зависит от конкретной реализации. Расширенные форматы предусматривают дополнительные биты для порядка (увеличенный диапазон) и мантиссы (повышенная точность). Таблица 8 содержит описание основных характеристик всех четырех форматов.
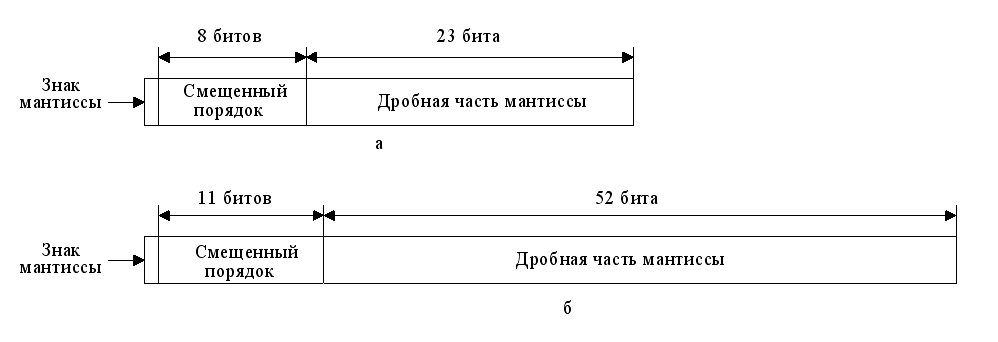
Рис. 24 Основные форматы IEEE 754: а – одинарный; б - двойной
Не все кодовые комбинации в форматах IEEE интерпретируются обычным путем — некоторые комбинации используются для представления специальных значений. Предельные значения порядка, содержащие все нули (0) и все единицы (255 — в одинарном формате и 2047 — в двойном формате), определяют специальные значения.
Описываются следующие классы чисел.
· Порядки в диапазоне от 1 до 254 для одинарного формата и от 1 до 2036 — для двойного формата, используются для представления ненулевых нормализованных чисел. Порядки смещены так, что их диапазон составляет от -126 до +127 для одинарного формата и от -1022 до +1023 — для двойного формата. Нормализованное число требует, чтобы слева от двоичной запятой был единичный бит. Этот бит подразумевается, благодаря чему обеспечивается эффективная ширина мантиссы, равная 24 битам для одинарного и 53 битам — для двойного форматов.
· Нулевой порядок совместно с нулевой мантиссой представляют положительный или отрицательный 0, в зависимости от состояния бита знака мантиссы.
· Порядок, содержащий единицы во всех разрядах, плюс нулевая мантисса соответствуют бесконечности (положительной или отрицательной, в зависимости от состояния бита знака), что позволяет пользователю самому решить, считать ли это ошибкой или продолжать вычисления со значением, равным бесконечности.
· Нулевой порядок в сочетании с ненулевой мантиссой обозначают ненормализованное число. В этом случае бит слева от двоичной точки равен 0 и фактический порядок равен -126 или -1022. Число является положительным или отрицательным в зависимости от значения знакового бита.
· Кодовая комбинация, в которой порядок содержит все единицы, а мантисса не равна 0, используется как признак «не числа» (NAN — Not a Number) и служит для предупреждения о различных исключительных ситуациях, например о делении 0/0.
Табл. 8 Параметры форматов стандарта IEEE 754
| Параметр | Формат | |||
| одинарный | одинарный раширенный | двойной | двойной расширенный | |
| Разрядность слова,бит | ≥43 | ≥79 | ||
| Поле порядка, бит | ≥11 | ≥15 | ||
| Смещение порядка | Не оговорено | Не оговорено | ||
| Поле мантиссы, бит | ≥31 | ≥63 | ||
| Максимальное значение порядка | ≥1023 | ≥16383 | ||
| Минимальное значение порядка | -126 | ≤-1022 | -1022 | ≤-16382 |
| Диапазон чисел | 10-38, 1038 | Не оговорен | 10-308, 10308 | Не оговорен |
Упакованные числа с плавающей запятой
В рамках уже упоминавшейся технологии SSЕ4 имеются команды, служащие для увеличения производительности систем при обработке мультимедийной информации, описываемой числами с ПЗ. Каждая такая команда работает с четырьмя операндами с плавающей запятой одинарной точности или двумя операндами двойной точности. Операнды упаковываются в 128-разрядные группы, как это показано на рис. 25.

Рис. 25 Формат упакованных чисел с плавающей запятой в технологии SSЕ4
Разрядность основных форматов числовых данных
Данные, представляющие в ВМ числовую информацию, могут иметь фиксированную или переменную длину. Операционные устройства вычислительных машин (целочисленные арифметико-логические устройства, блоки обработки чисел с плавающей запятой, устройства десятичной арифметики и т. п.), как правило, рассчитаны на обработку кодов фиксированной длины. Общепринятые величины разрядности кодов чисел: бит, полубайт, байт, слово, двойное слово, счетверенное слово, двойное счетверенное слово.
Наименьшей единицей данных в ВМ служит бит (BIT, Binary digiT — двоичная цифра). В большинстве случаев эта единица информации слишком мала. Однобитовые операционные устройства использовались в ВМ с последовательной обработкой информации, а в современных машинах с параллельной обработкой разрядов они практически не применяются. Побитовую работу с данными скорее можно встретить в многопроцессорных вычислительных системах, построенных из одноразрядных процессоров.
Следующая по величине единица состоит из четырех битов и называется полубайтом или тетрадой, или реже «ниблом» (nibble). Она также редко имеет самостоятельное значение и заслуживает упоминания как единица представления отдельных десятичных цифр при их двоично-десятичной записи.
Реально наименьшей обрабатываемой единицей считается байт (BYTE, BinarY TErm — двоичный элемент), состоящий из восьми битов. На практике эта единица информации также оказывается недостаточной, и значительно чаще применяются числа, представленные двумя (слово — 16 битов), четырьмя (двойное слово — 32 бита), восемью (счетверенное слово — 64 бита) или шестнадцатью (двойное счетверенное слово — 128 битов) байтами.
Блоки операций с плавающей запятой обычно согласованы со стандартом IEEE 754 и рассчитаны на обработку чисел в формате двойной длины (64 бита). В большинстве ВМ реальная разрядность таких блоков даже больше (80 битов). Таким образом, наилучшим вариантом при проведении вычислений с плавающей запятой можно считать формат двойного слова. При выборе формата меньшей длины (32 разряда) вычисления все равно ведутся с большей точностью, после чего результат округляется. Таким образом, использование короткого формата чисел с плавающей запятой, как и в случае целых чисел с фиксированной запятой, помимо экономии памятй никаких иных преимуществ также не дает.
В приложениях, оперирующих десятичными числами, где количество цифр в числе может варьироваться в широком диапазоне, что характерно для задач из области экономики, более удобными оказываются форматы переменной длины. В этом случае числа не переводятся в двоичную систему, а записываются в виде последовательности двоично-кодированных десятичных цифр. Длина подобной цепочки может быть произвольной, а для указания ее границы обычно используют символ-ограничитель, код которого не совпадает с кодами цифр. Длина цифровой последовательности может быть задана явно в виде количества цифр числа и храниться в первом байте записи числа, однако этот прием более характерен для указания длины строки символов.
Размещение числовых данных в памяти
В современных ВМ разрядность ячейки памяти, как правило, равна одному байту (8 битов), а реальная длина кодов чисел составляет 2,4,8 или 16 байтов. При хранении таких чисел в памяти их байты размещают в нескольких ячейках со смежными адресами, при этом для доступа к числу указывается только наименьший из адресов. При разработке архитектуры системы команд необходимо определить порядок размещения байтов в памяти, то есть какому из байтов (старшему или младшему) будет соответствовать этот наименьший адрес. На рис. 26 показаны оба варианта размещения 32-разрядного числа в четырех смежных ячейках памяти, начиная с адреса А.
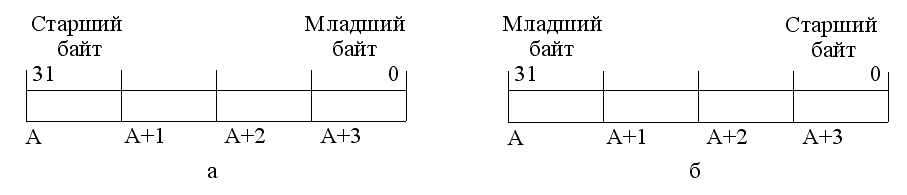
Рис. 26 Размещение в памяти 32-разрядного числа: а – начиная со старшего байта;
б – начиная с младшего байта
В вычислительном плане оба способа записи равноценны. Так, фирмы DEC и Intel отдают предпочтения размещению в первой ячейке младшего байта, a IBM и Motorola ориентируются на противоположный вариант. Выбор обычно связан с некими иными соображениями разработчиков ВМ. В настоящее время в большинстве машин предусматривается использование обоих вариантов, причем выбор может быть произведен программным путем за счет соответствующей установки регистра конфигурации.
Помимо порядка размещения байтов, существенным бывает и выбор адреса, с которого может начинаться запись числа. Связано это с физической реализацией полупроводниковых запоминающих устройств, где обычно предусматривается возможность считывания (записи) четырех байтов подряд. Причем данная операция выполняется быстрее, если адрес первого байта Aотвечает условию A mod S=0 (S= 2,4,8,16). Числа, размещенные в памяти в соответствии с этим правилом, называются выравненными (рис. 27).
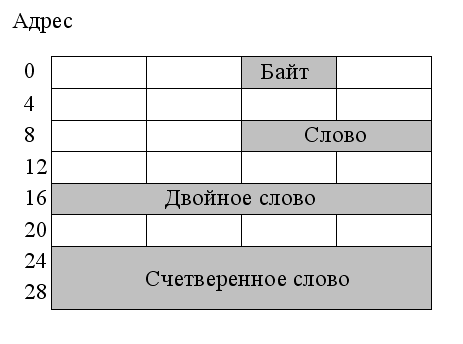
Рис. 27 Размещение чисел в памяти с выравниванием
На рис.28 показаны варианты размещения 32-разрядного двойного слова без выравнивания. Такое размещение приводит к увеличению времени доступа к памяти.
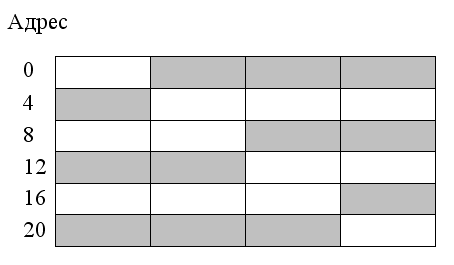
Рис. 28 Размещение 32-разрядного слова без соблюдения правила выравнивания
Большинство компиляторов генерируют код, в котором предусмотрено выравнивание чисел в памяти.
Символьная информация
В общем объеме вычислительных действий все большая доля приходится на обработку символьной информации, содержащей буквы, цифры, знаки препинания, математические и другие символы. Каждому символу ставится в соответствие определенная двоичная комбинация. Совокупность возможных символов и назначенных им двоичных кодов образует таблицу кодировки. В настоящее время применяются множество различных таблиц кодировки. Объединяет их весовой принцип, при котором веса кодов цифр возрастают по мере увеличения цифры, а веса символов увеличиваются в алфавитном порядке. Так вес буквы «Б» на единицу больше веса буквы «А». Это способствует упрощению обработки в ВМ.
До недавнего времени наиболее распространенными были кодовые таблицы, в которых символы кодируются с помощью восьмиразрядных двоичных комбинаций (байтов), позволяющих представить 256 различных символов:
· расширенный двоично-кодированный код EBCDIC (Extended Binary Coded Decimal Interchange Code);
· американский стандартный код для обмена информацией ASCII (American Standard Code for Information Interchange).
Код EBCDIC используется в качестве внутреннего кода в универсальных ВМ фирмы IBM. Он же известен под названием ДКОИ (двоичный код для обработки информации).
Стандартный код ASCII — 7-разрядный, восьмая позиция отводится для записи бита четности. Это обеспечивает представление 128 символов, включая все латинские буквы» цифры, знаки основных математических операций и знаки пунктуации. Позже помнилась европейская модификация ASCII, называемая Latin 1 (стандарт ISO 8859-1). В ней «полезно» используются все 8 разрядов. Дополнительные комбинации (коды 128-255) в новом варианте отводятся для представления специфических букв алфавитов западноевропейских языков, символов псевдографики, некоторых букв греческого алфавита, а также ряда математических и финансовых символом. Именно эта кодовая таблица считается мировым стандартом де-факто, который применяется с различными модификациями во всех странах. В зависимости от использования кодов 128-255 различают несколько вариантов стандарта ISO 8859 (табл.9).
Табл. 9 Варианты стандарта ISO 8859
| Стандарт | Характеристика | |
| ISO 8859-1 | Западноевропейские языки | |
| ISO 8859-2 | Языки стран центральной и восточной Европы | |
| ISO 8859-3 | Языки стран южной Европы, мальтийский и эсперанто | |
| ISO 8859-4 | Языки стран северной Европы | |
| ISO 8859-5 | Языки славянских стран с символами кириллицы | |
| ISO 8859-6 | Арабский язык | |
| ISO 8859-7 | Современный греческий язык | |
| ISO 8859-8 | Языки иврит и идиш | |
| ISO 8859-9 | Турецкий язык | |
| ISO 8859-10 | Языки стран северной Европы (лапландский, исландский) | |
| ISO 8859-11 | Тайский язык | |
| ISO 8859-12 | Языки балтийских стран | |
| ISO 8859-13 | Кельтский язык | |
| ISO 8859-14 | Комбинированная таблица для европейских языков | |
| ISO 8859-15 | Содержит специфические символы ряда языков: албанского, хорваского, английского, финского, французского, немецкого, венгерского, ирландского, итальянского, польского, румынского и словенского |
В распространенной в свое время операционной системе MS-DOS стандарт ISO 8859 реализован в форме кодовых страниц OEM (Original Equipment Manufacturer), Каждая OEM-страница имеет свой идентификатор (табл.10).
Табл. 10 Наиболее распространенные кодовые страницы OEM
| Индентификатор кодовой страницы | Страны | |
| CP437 | США, страны западной Европы и Латинской Америки | |
| CP708 | Арабские страны | |
| CP737 | Греция | |
| CP775 | Латвия, Литва, Эстония | |
| CP852 | Страны восточной Европы | |
| CP853 | Турция | |
| CP855 | Страны с кириллической письменностью | |
| CP860 | Португалия | |
| CP862 | Израиль | |
| CP865 | Дания, Норвегия | |
| CP866 | Россия | |
| CP932 | Япония | |
| CP936 | Китай |
Хотя код ASCII достаточно удобен, он все же слишком тесен и невмещает множества необходимых символов. По этой причине в1993 годуконсорциумом компаний Apple Computer, Microsoft, Hewlett-Packard, DEC иIBM былразработан 16-битовый стандарт ISO 10646, определяющий универсальный наборсимволов (UCS, Universal Character Set). Новый код, известный под названиемUnicode, позволяет задать до 65536 символов, то есть дает возможностьодновременно представить символы всех основных «живых» и «мертвых» языков. Длябукв русского языка выделены коды 1040-1093.
Все символы в Unicode логически разделяют на17 плоскостей по65536 (216) кодов в каждой.
· Плоскость 0 (0000-FFFF): BMP, Basic Multilingual Plane — основная многоязычная плоскость. Эта плоскость охватывает коды большинства основных символов используемых в настоящее время языков. Каждый символ представляется 16- разрядным кодом.
· Плоскость 1 (10000-1FFFF): SMP, Supplementary Multilingual Plane дополнительная многоязычная плоскость.
· Плоскость 2 (20000-2FFFF): SIP, Supplementary Ideographic Plane дополнительная идеографическая плоскость.
· Плоскости с 3 по 13 (30000-DFFF) пока не используются.
· Плоскость 14 (E0000-EFFFF): SSP, Supplementary Special-purpose Plane - специализированная дополнительная плоскость.
· Плоскость 15 (F0000-FFFFF): PUA, Private Use Area область дли частного использования.
· Плоскость 16 (100000-10FFFF): PUA, Private Use Area область для частного использования.
В настоящее используется порядка 10% потенциального пространства кодов.
В «естественном» варианте кодировки Unicode, известном как UCS-2, каждый символ описывается двумя последовательными байтами m и n, так что номеру символа соответствует численное значение 256×m + n. Таким образом, кодовый номер представлен 16-разрядным двоичным числом.
Наряду с UCS-2 в рамках Unicode существуют еще несколько вариантов кодировки Unicode (UTF, Unicode Transformation Formats), основные из которых UTF-32, UTF-16, UTF-8 и UTF-7.
В кодировке UTF-32 каждая кодовая позиция представлена 32-разрядным двоичным числом. Это очень простая и очевидная система кодирования, хотя и неэффективная в плане разрядности кода. Кодировка UTF-32 используется редко, главным образом, в операциях обработки строк для внутреннего представления данных.
UTF-16 каждую кодовую позицию для символов из плоскости BMP представляет двумя байтами. Кодовые позиции из других плоскостей представлены так называемой суррогатной парой. Представление основных символов одинаковым числом байтов очень удобно в том плане, что можно прямо адресоваться к любому символу строки.
В кодировке UTF-8 коды символов меньшие, чем 128, представляются одним байтом. Все остальные коды формируются по более сложным правилам. В зависимости от символа, его код может занимать от двух до шести байтов, причем старший бит каждого байта всегда имеет единичное значение. Иными словами, значение байта лежит в диапазоне от 128 до 255. Ноль в старшем бите байта означает, что код занимает один байт и совпадает по кодировке с ASCII. Схема формирования кодов UTF-8 показана в табл. 11.
Табл. 11 Структура кодов UTF-8
