Перевод правильной десятичной дроби в другую позиционную систему счисления

↑ Наверх

Правило перевода правильной десятичной дpоби F в систему счисления с основанием q.

Необходимо F умножить на q , записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q, и т. д., до тех пор, пока дробная часть очередного произведения не станет равной нулю, либо не будет достигнута требуемая точность изображения числа F в q-ичной системе. Представлением дробной части числа F в новой системе счисления будет последовательность целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой [2].

Если требуемая точность перевода числа F составляет k знаков после запятой, то предельная абсолютная погрешность при этом равняется q^-(k+1)/ 2.

Пример 3.3. Переведем число 0,42 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

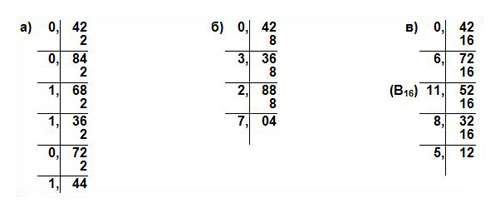
Ответ:

а) 0,42₁₀= 0,01101₂ с предельной абсолютной погрешностью 2^-6/2=2^-7;

б) 0,42₁₀=0,327₈ с предельной абсолютной погрешностью 8^-4/2=2^-13;

в) 0,42₁₀=0,6B85₂ с предельной абсолютной погрешностью 16^-5/2=2^-21.

Для чисел, имеющих целую и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для каждой из частей, а затем складываются.

Перевод числа в десятичную систему счисления

↑ Наверх

Правило перевода в десятичную систему числа X, записанного в q-ичной системе счисления в виде X_q = (a_n a_n-1 ...a₀ , a_-1 a_-2 ... a_-m)_q производится путем вычисления значения многочлена:

X₁₀ = a_n qⁿ + a_n-1 q^n-1 + ... + a₀ q⁰ + a_-1 q^-1 + a_-2 q^-2 + ... + a_-m q^-m ,

здесь n – номер разряда (считается от запятой влево начиная с 0); m – номер разряда дробной части (считается вправо от запятой, начиная с 1).

Пример 3.4.

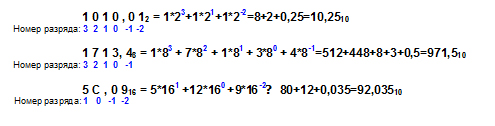
Арифметические операции в позиционных системах счисления

← 3.3. Перевод чисел из десятичной системы в...

3.5. Контрольные вопросы и задания →

Рассмотрим арифметические операции: сложение и вычитание.

Правила сложения и вычитания в десятичной системе применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.

Сложение

↑ Наверх

Таблицы сложения (рис. 3.1) составляются по правилу: при сложении цифры суммируются по разрядам справа налево, и если при этом возникает избыток, то он переносится влево.

Сложение в двоичной системе +	Сложение в шестнадцатеричной системе + A B C D E F A B C D E F A B C D E F A B C D E F A B C D E F A B C D E F A B C D E F A B C D E F A B C D E F A B C D E F A B C D E F A A B C D E F B B C D E F 1A C C D E F 1A 1B D D E F 1A 1B 1C E E F 1A 1B 1C 1D F F 1A 1B 1C 1D 1E
Сложение в восьмеричной системе +

Рис.3.1. Таблицы сложения

Пример 3.5. Сложим числа 1000111,01₂ + 101,11₂.

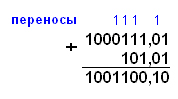
Ответ: 1000111,01₂ + 101,11₂ = 1001100,10₂.

Вычитание

↑ Наверх

Вычитание в других системах производится аналогично десятичной. Займ единицы из разряда слева равен основанию счисления, т.е. в восьмеричной – это займ 8 единиц, в шестнадцатеричной – шестнадцати.

Пример 3.6. Вычтем единицу из чисел 110,01₈ и 110,01₁₆.

В восьмеричной системе счисления

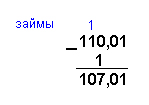
В шестнадцатеричной системе счисления

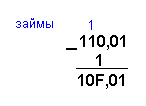
3.5. Контрольные вопросы и задания

← 3.4. Арифметические операции в позиционных...

4.Введение →

1. Какие системы счисления называют позиционными, а какие — непозиционными? Приведите примеры.

2. Что называется основанием системы счисления?

3. Почему для вычислительной техники особенно важна система счисления по основанию 2?

4. Какие символы используются для записи чисел в двоичной системе счисления; восьмеричной; шестнадцатеричной?

5. Чему равны веса разрядов слева от точки, разделяющей целую и дробную части, в двоичной системе счисления (восьмеричной; шестнадцатеричной)?

6. Чему равны веса разрядов справа от точки, разделяющей целую и дробную части, в двоичной системе счисления (восьмеричной; шестнадцатеричной)?

7. Как переводить числа из двоичного представления в восьмеричное и шестнадцатеричное представления и обратно?

8. Переведите в двоичную, восьмеричную и шестнадцатеричную системы десятичные числа 131, 504.

9. Переведите в десятичную систему двоичные числа 1011101, 1100,101.

10. Какое максимальное число можно представить в двоичной системе пятнадцатью цифрами?

11. Переведите в двоичную систему шестнадцатеричные числа 3АB, 14FC.

12. Сложите числа в двоичном представлении 1101101,1 и 1001,011.