Алфавитное неравномерное двоичное кодирование. Код Хаффмана

На этом шаге мы рассмотрим алфавитное неравномерное двоичное кодирование; префиксный код; код Хаффмана.

Равномерное кодирование удобно для декодирования. Однако часто применяют и неравномерные коды, т.е. коды с различной длиной кодовых слов. Это полезно, когда в исходном тексте разные буквы встречаются с разной частотой. Тогда часто встречающиеся символы стоит кодировать более короткими словами, а редкие – более длинными. Из примера 1 видно, что (в отличие от равномерных кодов!) не все неравномерные коды допускают однозначное декодирование.

Есть простое условие, при выполнении которого неравномерный код допускает однозначное декодирование.

Код называется префиксным, если в нем нет ни одного кодового слова, которое было бы началом (по-научному, - префиксом) другого кодового слова.

Код из примера 1 – НЕ префиксный, так как, например, код буквы А (т.е. кодовое слово 1) – префикс кода буквы К (т.е. кодового слова 12, префикс выделен жирным шрифтом).

Код из примера 2 (и любой другой равномерный код) – префиксный: никакое слово не может быть началом слова той же длины.

Пример . Пусть исходный алфавит включает 9 символов: А, Л, М, О, П, Р, У, Ы, -. Кодовый алфавит – двоичный. Кодовые слова:

А: 00 М: 01 -: 100 Л: 101 У: 1100 Ы: 1101 Р: 1110 О: 11110 П: 11111

Кодовые слова выписаны в алфавитном порядке. Видно, что ни одно из них не является началом другого. Это можно проиллюстрировать рисунком

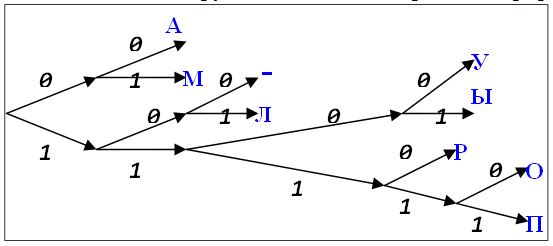На рисунке изображено бинарное дерево. Его корень расположен слева. Из каждого внутреннего узла выходит два ребра. Верхнее ребро имеет пометку 0, нижнее – пометку 1. Таким образом, каждому узлу соответствует слово в двоичном алфавите. Если слово X является началом (префиксом) слова Y, то узел, соответствующий слову X, находится на пути из корня в узел, соответствующий слову Y. Наши кодовые слова находятся в листьях дерева. Поэтому ни одно из них не является началом другого.

Символы некоторого первичного алфавита (например, русского) кодируются комбинациями символов двоичного алфавита (т.е. 0 и 1), причем, длина кодов и, соответственно, длительность передачи отдельного кода, могут различаться. Длительности элементарных сигналов при этом одинаковы ( ₀ = ₁ = ). За счет чего можно оптимизировать кодирование в этом случае? Очевидно, суммарная длительность сообщения будет меньше, если применить следующий подход: тем буквам первичного алфавита, которые встречаются чаще, присвоить более короткие по длительности коды, а тем, относительная частота которых меньше – коды более длинные. Но длительность кода – величина дискретная, она кратна длительности сигнала передающего один символ двоичного алфавита. Следовательно, коды букв, вероятность появления которых в сообщении выше, следует строить из возможно меньшего числа элементарных сигналов. Построим кодовую таблицу для букв русского алфавита, основываясь на приведенных ранее вероятностях появления отдельных букв.

Очевидно, возможны различные варианты двоичного кодирования, однако, не все они будут пригодны для практического использования – важно, чтобы закодированное сообщение могло быть однозначно декодировано, т.е. чтобы в последовательности 0 и 1, которая представляет собой многобуквенное кодированное сообщение, всегда можно было бы различить обозначения отдельных букв. Проще всего этого достичь, если коды будут разграничены разделителем – некоторой постоянной комбинацией двоичных знаков. Условимся, что разделителем отдельных кодов букв будет последовательность 00 (признак конца знака), а разделителем слов – 000 (признак конца слова – пробел). Довольно очевидными оказываются следующие правила построения кодов:

• код признака конца знака может быть включен в код буквы, поскольку не существует отдельно (т.е. кода всех букв будут заканчиваться 00);
• коды букв не должны содержать двух и более нулей подряд в середине (иначе они будут восприниматься как конец знака);
• код буквы (кроме пробела) всегда должен начинаться с 1;
• разделителю слов (000) всегда предшествует признак конца знака; при этом реализуется последовательность 00000 (т.е. если в конце кода встречается комбинация …000 или …0000, они не воспринимаются как разделитель слов); следовательно, коды букв могут оканчиваться на 0 или 00 (до признака конца знака).

Длительность передачи каждого отдельного кода t_i, очевидно, может быть найдена следующим образом: t_i = k_i • , где k_i – количество элементарных сигналов (бит) в коде символа i. В соответствии с приведенными выше правилами получаем следующую таблицу кодов:

Таблица 1. Таблица кодов
Буква	Код	pi·103	ki	Буква	Код	pi·103	ki
пробел				я
о				ы
е				з
а				ь,ъ
и				б
т				г
н				ч
с				й
р				х
в				ж
л				ю
к				ш
м				ц
д				щ
п				э
у				ф

Теперь по формуле можно найти среднюю длину кода K⁽²⁾ для данного способа кодирования:

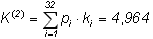
Поскольку для русского языка, I₁^(r)=4,356 бит, избыточность данного кода, согласно (2), составляет:

Q^(r) = 1 - 4,356/4,964 0,122;

это означает, что при данном способе кодирования будет передаваться приблизительно на 12% больше информации, чем содержит исходное сообщение. Аналогичные вычисления для английского языка дают значение K⁽²⁾ = 4,716, что приI₁^(e) = 4,036 бит приводят к избыточности кода Q^(e) = 0,144.

Наиболее простыми и употребимыми кодами такого типа являются так называемые префиксные коды, которые удовлетворяют следующему условию (условию Фано):

Неравномерный код может быть однозначно декодирован, если никакой из кодов не совпадает с началом (префиксом) какого-либо иного более длинного кода.

Например, если имеется код 110, то уже не могут использоваться коды 1, 11, 1101, 110101 и пр. Если условие Фано выполняется, то при прочтении (расшифровке) закодированного сообщения путем сопоставления со списком кодов всегда можно точно указать, где заканчивается один код и начинается другой.

Пример. Пусть имеется следующая таблица префиксных кодов:

Таблица 2. Таблица кодов
а	л	м	р	у	ы

Требуется декодировать сообщение: 00100010000111010101110000110.

Декодирование производится циклическим повторением следующих действий.

1. Отрезать от текущего сообщения крайний левый символ, присоединить к рабочему кодовому слову.

2. Сравнить рабочее кодовое слово с кодовой таблицей; если совпадения нет, перейти к (1).

3. Декодировать рабочее кодовое слово, очистить его.

4. Проверить, имеются ли еще знаки в сообщении; если "да", перейти к (1).

Применение данного алгоритма дает:

Доведя процедуру до конца, получим сообщение: "мама мыла раму".

Таким образом, использование префиксного кодирования позволяет делать сообщение более коротким, поскольку нет необходимости передавать разделители знаков. Однако условие Фано не устанавливает способа формирования префиксного кода и, в частности, наилучшего из возможных.

Способ оптимального префиксного двоичного кодирования был предложен Д.Хаффманом. Построение кодов Хаффмана мы рассмотрим на следующем примере: пусть имеется первичный алфавит A, состоящий из шести знаков a₁, ..., a₆ с вероятностями появления в сообщении, соответственно, 0,3; 0,2; 0,2; 0,15; 0,1; 0,05. Создадим новый вспомогательный алфавит A₁, объединив два знака с наименьшими вероятностями (a₅ и a₆) и заменив их одним знаком (например, a⁽¹⁾); вероятность нового знака будет равна сумме вероятностей тех, что в него вошли, т.е. 0,15; остальные знаки исходного алфавита включим в новый без изменений; общее число знаков в новом алфавите, очевидно, будет на 1 меньше, чем в исходном. Аналогичным образом продолжим создавать новые алфавиты, пока в последнем не останется два знака; ясно, что число таких шагов будет равно N – 2, где N – число знаков исходного алфавита (в нашем случае N = 6, следовательно, необходимо построить 4 вспомогательных алфавита). В промежуточных алфавитах каждый раз будем переупорядочивать знаки по убыванию вероятностей. Всю процедуру построения представим в виде таблицы:

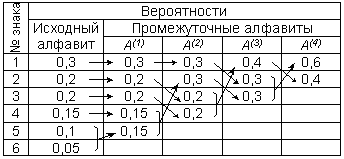
Теперь в обратном направлении поведем процедуру кодирования. Двум знакам последнего алфавита присвоим коды 0 и 1 (которому какой – роли не играет; условимся, что верхний знак будет иметь код 0, а нижний – 1). В нашем примере знак a₁⁽⁴⁾ алфавита A⁽⁴⁾, имеющий вероятность 0,6 , получит код 0, а a₂⁽⁴⁾ с вероятностью 0,4 – код 1. В алфавите A⁽³⁾знак a₁⁽³⁾ с вероятностью 0,4 сохранит свой код (1); коды знаков a₂⁽³⁾ и a₃⁽³⁾, объединенных знаком a₁⁽⁴⁾ с вероятностью 0,6 , будут уже двузначным: их первой цифрой станет код связанного с ними знака (т.е. 0), а вторая цифра – как условились – у верхнего 0, у нижнего – 1; таким образом, a₂⁽³⁾ будет иметь код 00, а a₃⁽³⁾ – код 01. Полностью процедура кодирования представлена в следующей таблице:

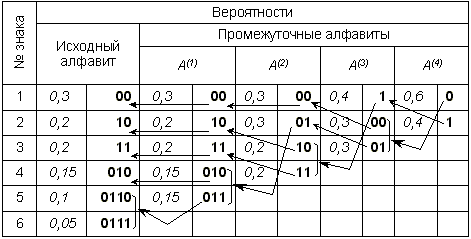
Из самой процедуры построения кодов легко видеть, что они удовлетворяют условию Фано и, следовательно, не требуют разделителя. Средняя длина кода при этом оказывается:

K⁽²⁾ = 0,3·2+0,2·2+0,2·2+0,15·3+0,1·4+0,05·4 = 2,45.

Для сравнения можно найти I₁^(A) – она оказывается равной 2,409, что соответствует избыточности кода Q = 0,0169, т.е. менее 2%.

Код Хаффмана важен в теоретическом отношении, поскольку можно доказать, что он является самым экономичным из всех возможных, т.е. ни для какого метода алфавитного кодирования длина кода не может оказаться меньше, чем код Хаффмана.

Применение описанного метода для букв русского алфавита дает следующие коды:

Таблица 3. Таблица кодов русских букв
Буква	Код	pi·103	ki	Буква	Код	pi·103	ki
пробел				я
о				ы
е				з
а				ь,ъ
и				б
т				г
н				ч
с				й
р				х
в				ж
л				ю
к				ш
м				ц
д				щ
п				э
у				ф

Средняя длина кода оказывается равной K⁽²⁾ = 4,395; избыточность кода Q^(r) = 0,00887, т.е. менее 1%.

Таким образом, можно заключить, что существует метод построения оптимального неравномерного алфавитного кода. Не следует думать, что он представляет число теоретический интерес. Метод Хаффмана и его модификация – метод адаптивного кодирования (динамическое кодирование Хаффмана) – нашли широчайшее применение в программах-архиваторах, программах резервного копирования файлов и дисков, в системах сжатия информации в модемах и факсах.