Постановка задачи оптимизации
Государственное бюджетное образовательное учреждение
Высшего профессионального образования города Москвы
«Московский городской педагогический университет»
Институт математики и информатики
Кафедра прикладной информатики
КУРСОВАЯ РАБОТА
по дисциплине «Методы оптимизации в управлении»
Тема: «Разработка машинного алгоритма и программы многомерной оптимизации для градиентного метода с использованием метода равномерного поиска».
Выполнил:
студент группы ПИНФБ-ОД-02
Ерёмин Иван Денисович
Руководитель:
Федин Ф.О., доцент, к.в.н.
Москва
Содержание
Введение. 2
Глава I. Теоретическая часть. 3
1. Постановка задачи оптимизации. 4
1.1. Необходимые и достаточные условия экстремума. 4
1.2. Характеристика класса задачи и ее место в общей классификации оптимизационных задач. 4
1.3. Описание метода решения и расчетного алгоритма. 5
Глава II. Практическая часть. 7
2. Разработка компьютерной программы для решения задачи оптимизации градиентным методом с использованием равномерного поиска. 7
2.1. Разработка блок-схемы машинного алгоритма и программы.. 7
2.2. Проверка необходимых и достаточных условий экстремума для найденной точки минимума. 12
2.3. Разработки программы проверки ограничений. 14
Заключение. 15
Список литературных источников. 16
Отзыв научного руководителя. 17
Введение
Область применения оптимизационных задач чрезвычайно широка, любая деятельность связана с решением задач оптимизации. К примеру, это такие сферы как: распределение ресурсов в экономике, управленческие решения в социальной сфере, проектирование технических устройств и систем и это лишь некоторые сферы.
Целью курсового проекта является применение полученных в данном курсе знаний и умений на практике при решении задачи оптимизации с использованием современного инструментария на основе встроенного прикладного программного обеспечения вычислительных систем.
Задачи к выполнению курсовой работы:
1. Проверить необходимые условия существования экстремума многомерной функции для своего варианта функции. Воспользоваться средствами Mathcad, составив программу.
2. Проверить достаточные условия существования экстремума многомерной функции для своего варианта функции. Воспользоваться средствами Mathcad, составив программу.
3. Разработать машинный алгоритм и программу в Mathcad многомерной оптимизации.
4. Определить по составленной программе в Mathcad экстремум функции.
5. Проверить ограничения используя программу в Mathcad.
Исходные данные:
Целевая функция: Z(x, y) = F(x) + H(y), где

Критерий оптимизации: точка экстремума (локальный экстремум)
Метод оптимизации: градиентный метод с использованием метода равномерного поиска.
Компьютерные средства:Вычислительная среда Mathcad.
Глава I. Теоретическая часть
Постановка задачи оптимизации
Оптимизация – выбор предпочтительного варианта проекта по принятым критериям.
В основе оптимизации лежит функция цели Z(x,y), которая строиться на основе суммы двух других целевых функций 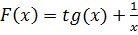 и
и
 , и характеризует качество объекта.
, и характеризует качество объекта.
