А – это десять в десятичной системе, плюс 7 получается 17, что соответствует 11 в шестнадцатеричной системе. Один пишем, один в уме

Практическое занятие. Системы счисления. Арифметические операции в различных системах счисления

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

УФА – 2012

УДК 378.144.004.45

ББК 74.58:32.973

М 54

Рекомендовано к изданию методической комиссией факультета информационных технологий и управления БГАУ

(протокол № ____ от _________ 20___ г.)

Составитель: старший преподаватель Перегудова М.А,

ассистент Саттарова С.Ф.

Рецензент: к.т.н доцент Агишев Т.Х.

Ответственный за выпуск: заведующая кафедрой информатики и информационных технологий к.х.н. доцент Беляева А.С.

г.Уфа, БГАУ, Кафедра информатики и информационных технологий

Цель занятия

Сформировать у студентов понятия системы счисления, основания системы счисления и правил перевода чисел из одной системы счисления в другую.

Задачи занятия

Научиться переводить числа из одной системы счисления в другую, выполнять арифметические операции в различных системах счисления.

Основные положения

Системой счисления (СС) называется способ представления чисел посредством цифровых знаков. В качестве цифровых знаков используются арабские и римские цифры.

СС делятся на позиционные и непозиционные. В позиционных СС значение цифры зависит от ее положения в числе, а в непозиционных - не зависит. Примером непозиционной СС может служить римская. В качестве цифр в ней используются: I (1), V (5), X (10), L (50), C (100), D (500), M (1000) и т.д. Значение цифры не зависит от ее положения в числе. Например, в числе XXXII (32) X встречается трижды и в каждом случае обозначает одну и ту же величину – число 10.

В позиционной системе счисления количественное значение цифры зависит от ее позиции в числе. Например, в десятичной СС в числе 313 левая цифра 3 обозначает число сотен, а правая 3 – единиц.

Основание позиционной системы счисления – это количество цифр, используемых для формирования данной системы счисления. Поскольку за основание системы счисления можно принять любое натуральное число, то существует бесчисленное множество позиционных систем счисления.

Система счисления по основанию 2 называется двоичной, 3 – троичной, 4 – четверичной и т.д. В двоичной системе счисления используются цифры 0,1; в троичной – 0,1,2; в четверичной – 0,1,2,3 и т.д. В связи с этим можно заполнить следующую таблицу:

Основание СС	Алфавит
	0,1
	0,1,2
	0,1,2,3
… …	… 0,1,2,…,9 …
… …	… 0,1,2,3,4,6,7,8,9,A,B,C,D,E,F …
q	0,1,2, … q–1

В этих системах значение цифры определяется местом (позицией), где она стоит в числе.

Запись чисел в любой из позиционных систем счисления с основанием q означает сокращенную запись выражения:

a_n-1 • q^n-1 + a_n-2 • q^n-2 + … + a₁ • q¹ + a₀ • q⁰+a_-1•q^-1+ a_-2•q^-2+…+ a_-2•q^-s, где

q – основание системы счисления;

a_i – цифры из системы счисления;

n – число разрядов (целых);

s – число разрядов (дробных).

Например, 245,71=2•10²+4•10¹+5•10⁰+7•10^-1+1•10^-2

Существуют правила перевода из одной позиционной системы счисления в другую, которые рассмотрены в следующих примерах.

Пример 1. Перевести число 235,56 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную.

Решение.Для перевода целой части десятичного числа n в систему счисления с основанием q необходимо последовательно выполнять деление n на q с остатком, пока не получится неполное частное, меньшее делителя. Затем составить число из остатков, записывая их, начиная с последнего частного.

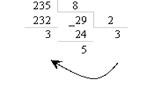
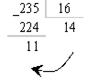
В шестнадцатеричной системе остаток 11 записывается цифрой В, а остаток 14 – цифрой Е.

После перевода целой части получается 235₁₀=11101011₂=353₈=ЕВ_16.

Для перевода дробной части числа n в систему счисления q следует эту часть числа умножать на основание системы q до тех пор, пока дробная часть очередного произведения не станет равной нулю, либо не будет достигнута требуемая точность. Число составляется из целых частей произведения, начиная с целой части первого произведения.

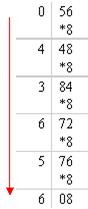
В шестнадцатеричной системе целая часть 15 записывается цифрой F, а остаток 12 – цифрой C. После перевода дробной части получается:

0,56₁₀= 0,10001₂= 0,43656₈= 0,8F5C2_16. Следовательно:

235,56₁₀=11101011,10001₂=353,43656₈=ЕВ,8F5C2_16.

Пример 2. Перевести числа:

§ 110110,101 из двоичной системы в десятичную;

§ 374,16 из восьмеричной системы в десятичную;

§ А8F,Е3 из шестнадцатеричной системы в десятичную.

Решение.Перевод в десятичную систему числа N, записанного в системе с основанием R, производится по формуле:

N_MN_M-1…N₁N₀,N_-1N_-2…N_-K=N_M*R^M+N_M-1*R^M-1+...+N₁*R¹+N₀*R⁰+N_-1*R^-1+

+N_-2*R^-2…+N-_K*R^-K

В нашем случае:

110110,101₂=1*2⁵+1*2⁴+0*2³+1*2²+1*2¹+0*2⁰+1*2^-1+0*2^-2+1*2^-3= =32+16+0+4+2+0+0,5+0+0,125=54,625 ₁₀

374,16₈=3*8²+7*8¹+4*8⁰+1*8^-1+6*8^-2= 192+56+4+0,125+0,094=252,219 ₁₀

А8F,Е3₁₆=А*16²+8*16¹+F*16⁰+E*16^-1+3*16^-2 = 10*16² + 8*16¹ + 15*16⁰ + 14*16^-1 + +3*16^-2 = 2560 + 128 + 15 + 0,875 + 0,012 = 2703,887 ₁₀

Пример 3. Выполнить сложение чисел в различных системах счисления:

§ 10001101,101₂+1110110,11₂;

§ 47214,15₈+673,315₈;

§ 1E7F,9A₁₆+355,B7₁₆.

Решение. Сложение чисел происходит по тем же правилам, что и в десятичной СС: цифры суммируются по разрядам, если возникает избыток, то он переносится влево.

Рассуждать, например, для шестнадцатеричной системы, можно следующим образом:

А – это десять в десятичной системе, плюс 7 получается 17, что соответствует 11 в шестнадцатеричной системе. Один пишем, один в уме.