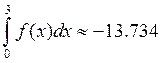Геометрическая интерпретация определенных интегралов

Понятие об М-файлах

Более эффективным способом выполнения команд в системе MATLAB является применение М-файлов.

М-файлом называется текстовый файл с расширением .m, содержащий набор инструкций на языке системы MATLAB (т.е. в М-файлах хранятся программные коды). Для решения различных математических задач MATLAB предоставляет весьма мощный и удобный язык программирования высокого уровня, интуитивно понятный даже для пользователей, не являющихся профессиональными программистами. Вместе с тем цель последующего изложения, разумеется, не начать осваивать с нуля новый и неизвестный язык программирования MATLAB. Несмотря на то, что работу в командной строке нельзя назвать программированием, тем не менее, все команды, операторы и функции, описанные ранее, составляют типичный инструментарий языка программирования системы MATLAB.

Поясним, что создать М-файл можно в любом текстовом редакторе, поддерживающим формат ASCII-файлов (например, текстовый процессор Microsoft Word). Вместе с тем, в системе MATLAB имеется собственный, рекомендуемый к использованию встроенный редактор М-файлов, который отличают удобные визуальные средства создания и отладки программ. В этом редакторе можно набрать команды, выполнить их сразу или частично, а после сохранить в файле, который можно использовать в дальнейшем.

М-файлы должны иметь уникальные имена. Длина имени при этом не ограничивается, но при идентификации имени учитываются лишь первые 31 символ. При исполнении программного объекта его имя сравнивается со списком имён, хранящихся в рабочей области и в директориях М-файлов. Если имя файла оказывается неуникальным, соответствующий программный объект не исполняется и выдаётся сообщение об ошибке, а если уникальным, то программный объект исполняется в интерпретирующем режиме.

Типы М-файлов

В системе MATLAB существуют два типа М-файлов: файл-программы (Script M-Files, скрипты или сценарии) и файл-функции (Function M-Files).

Файл-программы являются самым простым типом М-файлов ввиду того, что состоят из последовательности команд и не имеют входных и выходных аргументов (параметров). В процессе выполнения файл-программы не компилируются, они весьма полезны для автоматизации выполнения большого набора инструкций. В целом, файл-программы представляют собой зафиксированную в виде файла последовательность операций, полностью аналогичную той, которая используется в сессии.

В файл-функциях описываются функции, определяемые пользователем. В отличие от файл-программ, файл-функции могут принимать исходные данные в виде набора входных параметров и выдавать результаты в виде набора выходных значений. Файл-функции, являющиеся типичными полноценными объектами языка программирования системы MATLAB (и одновременно полноценными модулями с позиций структурного программирования), как правило, применяют при решении разного рода задач с использованием численных методов. Файл-функция служит средством расширения системы MATLAB. При обнаружении файл-функции она сначала компилируется, а затем исполняется (созданные машинные коды хранятся при этом в рабочей области системы MATLAB).

Основное отличие между файл-программами и файл-функциями состоит в работе с переменными. В частности, файл-программы работают только с переменными рабочего пространства и не имеют локальных переменных, т.е. все переменные, определённые в файл-программе, после её выполнения становятся доступными в рабочем пространстве и могут быть использованы в других файл-программах или командах, вводимых в командной строке (аналогично в файл-программе могут быть использованы все переменные, уже определённые в командном окне, т.е. файл-программа работает с данными рабочей области). Таким образом, рабочее пространство становится общим для всех файл-программ, используемых в текущем сеансе работы с MATLAB. Достоинством такого подхода является достигаемая в результате полная интеграция файл-программы с рабочим пространством, что делает файл-программы средством автоматизации интерактивного режима работы пользователя с системой MATLAB. Указанная интеграция является при этом и недостатком — так, например, если предполагается оформить в виде файл-программы отдельный фрагмент решения некоторой задачи, его следует всегда вызывать в одной и той же программной обстановке (что, очевидно, выполняется далеко не всегда). Кроме того, файл-программе в момент её вызова нельзя передать в виде параметров дополнительную информацию, не содержащуюся в рабочем пространстве. При выполнении нескольких файл-программ также исключительно важно следить за тем, чтобы в них были согласованы общие переменные.

Перечисленные слабые стороны файл-программ преодолеваются посредством использования файл-функций, которые, впрочем, слабо подготовлены для автоматизации интерактивного режима работы, так как переменные, используемые в файл-функциях, являются полностью изолированными от рабочего пространства MATLAB. Все переменные, используемые внутри файл-функции, а также опреденённые в качестве её входных и выходных аргументов, воспринимаются программой как локальные и доступны только лишь в теле данной файл-функции. Итак, после выполнения файл-функции все значения этих переменных исчезают, а область оперативной памяти, в которой они хранились, освобождается.

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Геометрическая интерпретация определенных интегралов

Пусть 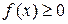на отрезке [a, b], тогда

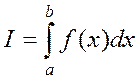
представляет собой площадь области, ограниченной осью х, графиком функции 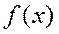и прямыми x=a и x=b.

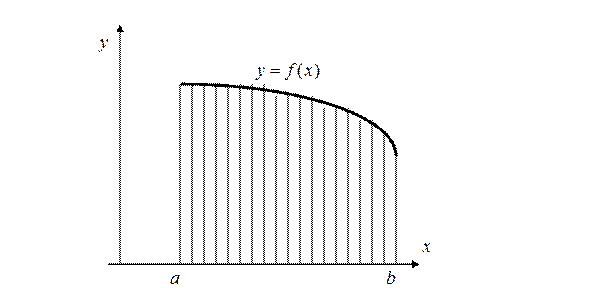
1. Метод средних прямоугольников

,

,

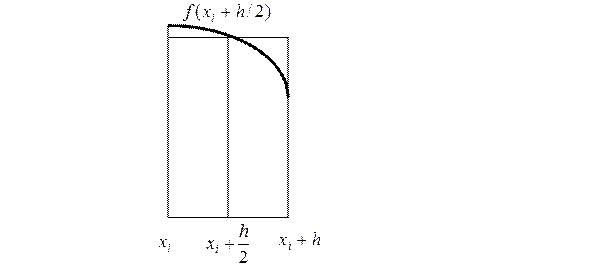
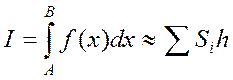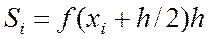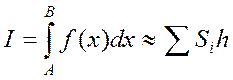
2. Метод трапеций

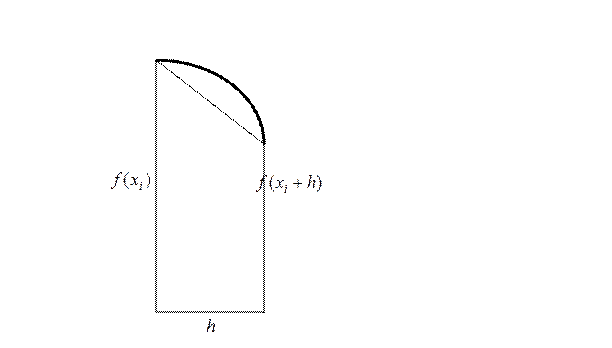
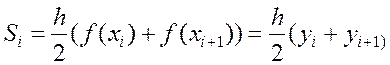
3. Метод Симпсона

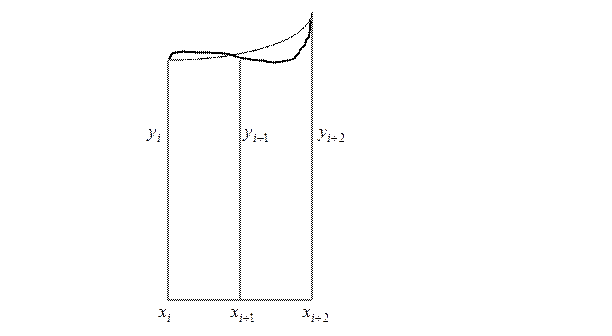
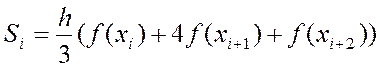
Вычислить

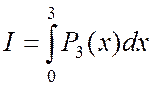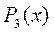,где - полином 3-ей степени.

Пример

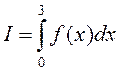,где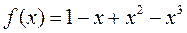

Ручной счет: n=4, h=(3-0)/4=0.75

а) Метод средних прямоугольников

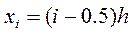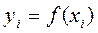, , i=1,2,3,4

I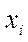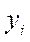
	0.375	0.713
	1.125	-0.283
	1.875	-3.951
	2.625	-12.822

I=0.75(0.713-0.283-3.951-12.822)=-12.258

Ответ: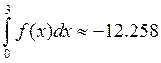

б) Метод трапеций:

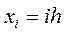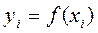, , i=0,1,2,3,4

I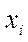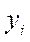
	0.0	1.0
	0.75	0.391
	1.5	-1.625
	2.25	-7.578
	3.0	-20.0

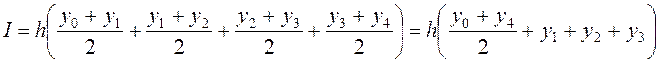
I=0.75((1.0-20)/2+0.391-1.625-7.578)=-13.734

Ответ: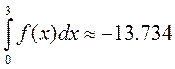

в) Метод Симпсона:

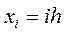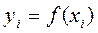, , i=0,1,2,3,4

I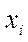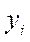
	0.0	1.0
	0.75	0.391
	1.5	-1.625
	2.25	-7.578
	3.0	-20.0

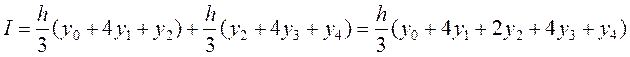
I=0.75/3(1.0+4*0.391+2*(-1.625)+4*(-7.578)-20.0)=-12.749

Ответ: