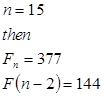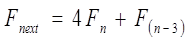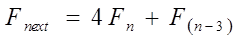Кролики в открытом космосе, или

ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ

Работа с теорией Эллиота немыслима без хотя бы поверхностного представления о том, что такое последовательность Фибоначчи. Леонард Фибоначчи – один из величайших математиков Средневековья. Говорят, что это свое открытие он сделал, задавшись вопросом: "Сколько кроликов, помещенных в клетку, можно получить в год от одной пары, если каждая пара производит новую каждый месяц, начиная со второго?". Любое из чисел последовательности Фибоначчи представляет собой количество пар кроликов в соответствующий месяц (обозначаемый порядковым номером). Начиная с единицы, каждый член последовательности равен сумме двух предыдущих. Числовой ряд, получающийся в результате, неограничен сверху (может продолжаться до бесконечности). Задается же эта последовательность следующим образом:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, …

Здравый смысл подсказывает, что ее можно слегка видоизменить. Я добавил к число 0 и получил в результате следующую арифметическую прогрессию:

Число Фибоначчи, F 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610

Порядковый номер числа, n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

Каждое число последовательности обладает двумя характеристиками: собственно значением F (количество кроликов) и порядковым номером n (дата фиксации этого количества – определенный месяц). Таким образом, если

Я бы советовал всем еще не читавшим просмотреть работы Роберта Пречтера, в которых кратко, но понятно обсуждается последовательность Фибоначчи со всеми своими удивительными свойствами, имеющими почти мистическое значение. Именно ему (Пречтеру) принадлежат знаменитые слова: "Когда Эллиот говорил о законах природы, он имел в виду последовательность Фибоначчи как математический базис теории волн".

Для целей данной дискуссии имеет особое значение следующее:

· Я включил в последовательность нулевое значение как четное число.

· Сама последовательность состоит из четных чисел, каждое из которых является суммой двух предыдущих нечетных.

· Каждая степень базисной волновой структуры Эллиота состоит из четного числа волн F, в свою очередь раскладывающегося на импульс длиною F(n-1) и коррективу размером F(n-2) (2 предыдущих нечетных значения).

· Последовательность не должна начинаться цифрой 1. Начальным ее членом может быть любое целое либо дробное число, удовлетворяющее соотношениям, существующим между всеми членами последовательности.

· Цифра 4, сама по себе в данную последовательность не входящая, очень все же важна.

· Числа Фибоначчи применяются к частотам, а не периодам волн Эллиота (и в его, и в моем анализе).

· Наиболее важные соотношения Фибоначчи, служащие для связи принципов Эллиота и циклистов, выглядят следующим образом:

Что же до кроликов, то Пречтер посчитал, что при длительности эксперимента, равной ста месяцам, число их увеличится до размеров в буквальном смысле этого слова просто астрономических. При принятии средних размеров среднего кролика за 1 кубический фут (0,028372625 кубометра) весь образовавшийся бы в течение 100 месяцев выводок, плечом к плечу и хвостом к носу поставленный, плотненько заполнил бы собой всю целиком территорию Италии. Если же выстроить их по вертикали, высота такой пирамиды составила бы примерно 22 000 миль (35 398 км). Такой способ построения вывел бы их на околоземную орбиту, туда, где силы притяжения уже почти не действуют. Самый резвый из них мог бы даже выпрыгнуть в открытый космос! К счастью, у нас есть модель процесса (последовательность Фибоначчи) – чтобы узнать все это, эксперимент проводить не надо.