Ешение матричной игры сведением к задаче линейного программирования с помощью программы Simplex Solver

αi = min hij	V1 = max αii
-3
-1

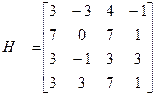
βj = max hij
V2 = min βii

1≤V(H) ≤3

С помощью доминирования игра свелась к игре размерности [3х2]

Среди элементов матрицы есть отрицательные → t=│min hij│+1

t=│-1│+1=2

H_t = H+t

H_t =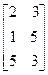

ЗЛП для игрока 1:

min [ f0 (х)=х1+х2+х3]

Х c R

R={Х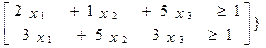

X≥0

R=X

ЗЛП для игрока 2:

max [ g0(y)=y1+y2]

Q=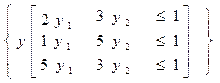

y≥0

	Хб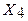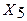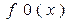
Xсв	УСВ Уб	-Y1	-Y2	Cj
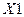	Y3
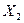	Y4
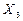	Y5
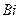	g0(y)	- 1	- 1

Обратный переход:

С помощью программы Simplex Solver получено решение

Х= (0;0,09;0,18;0;0),

Y=(0,09;0,18;0;0;0).

g₀(y*)=f₀(x*)=0,27

V(H)=1/f0(x*)=1/g0(y*)=1/0,27=3,7

V(H)=V(H_t)t-t=3,704-2=1,704

X^*=X*V(H)t

Y^*=Y*V(H_t)t

X₁=0*3,704=0

X₂=0,09*3,704=1/3

X₃=0,18*3,704=2/3

Y₁=0,09*3,704=1/3

Y₂=0,18*3,704=2/3

Ответ: X* = (0;0,09;0,18;0;0), Y* = (0,09;0,18;0;0;0),V(H) = 5/3, V(H)=1,7.

Задание №3

Разбор ситуации об инвестировании предприятий и освоение методики обоснования решения об инвестировании предприятия.

Задача:

На развитие трех предприятий выделено 5 млн. руб. Известна эффективность капитальных вложений в каждое предприятие, заданная значением нелинейной функции g_i(x_i), представленной в табл. 1

Таблица 1

x	g1	g2	g3
	2,2		2,8
		3,2	5,4
	4,1	4,8	6,4
	5,2	6,2	6,6
	5,9	6,4	6,9

Необходимо распределить выделенные средства между предприятиями таким образом, чтобы получить максимальный суммарный доход.

Для упрощения расчетов предполагаем, что распределение средств осуществляется в целых числах x_i = {0, 1, 2, 3, 4, 5} млн. руб.

Решение.

I этап. Условная оптимизация.

1-й шаг: k = 3. Предположим, что все средства в количестве x₃ = 5 млн. руб. отданы третьему предприятию. В этом случае максимальный доход, как это видно из табл. 2, составит g₃(x₃) = 6,9 тыс. руб., следовательно: F₃(C₃) = g₃(x₃).

Таблица 2

x3 C3							F3(C3)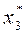
		2,8					2,8
			5,4				5,4
				6,4			6,4
					6,6		6,6
						6,9	6,9

2-й шаг: k = 2. Определяем оптимальную стратегию при распределении денежных средств между вторым и третьим предприятиями. При этом рекуррентное соотношение Беллмана имеет вид:

,

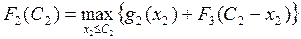на основе которого составлена табл. 3.

Таблица 3

х2 С2							F2(C2)
	0 + 0
	0 + 2,8	2 + 0					2,8
	0 + 5,4	2 + 2,8	3,2 + 0				5,4
	0 + 6,4	2 + 5,4	3,2 + 2,8	4,8 + 0			7,4
	0 + 6,6	2 + 6,4	3,2 + 5,4	4,8 + 2,8	6,2 + 0		8,6
	0 + 6,9	2 + 6,6	3,2 + 6,4	4,8 + 5,4	6,2 + 2,8	6,4 + 0	10,2

3-й шаг: k = 1. Определяем оптимальную стратегию при распределении денежных средств между первым и двумя другими предприятиями, используя следующую формулу для расчета суммарного дохода:

,

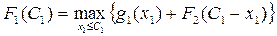на основе которого составлена табл. 4.

Таблица 4

х1 С1							F1(C1)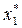
	0 + 0
	0 + 2,8	2,2 + 0					2,8
	0 + 5,4	2,2 + 2,8	3 + 0				5,4
	0 + 7,4	2,2 + 5,4	3 + 2,8	4,1 + 0			7,6
	0 + 8,6	2,2 + 7,4	3 + 5,4	4,1 + 2,8	5,2 +0		9,6
	0 + 10,2	2,2 + 8,6	3 + 7,4	4,1 + 5,4	5,2 + 2,8	5,9 + 0	10,8

II этап. Безусловная оптимизация.

Определяем компоненты оптимальной стратегии.

1-й шаг. По данным из табл. 4 максимальный доход при распределении 5 млн. руб. между тремя предприятиями составляет: C₁ = 5, F₁(5) = 10,8.

При этом первому предприятию нужно выделить 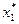= 1 млн руб.

2-й шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю второго и третьего предприятий: С₂ = C₁ – 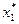= 5 – 1 = 4 млн руб.

По данным табл. 3 находим, что оптимальный вариант распределения денежных средств размером 4 млн. руб. между вторым и третьим предприятиями составляет: F₂(4) = 8,6 при выделении второму предприятию 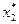= 2 млн руб.

3-й шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю третьего предприятия: С₃ = C₂ – 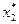= 4 – 2 = 2 млн руб.

По данным табл. 2 находим: F₃(2) = 5,4 и 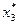= 2 млн руб.

Таким образом, оптимальный план инвестирования предприятий:

Х^* = (1, 2, 2), который обеспечит максимальный доход, равный

F(5) = g₁(l) + g₂(2) + g₃(2) = 2,2 + 3,2 + 5,4 = 10,8 млн руб.