Анализ и разработка алгоритма
Курсовая работа
по курсу «Технология программирования»
на тему: «Объектно-ориентированная технология программирования»
Вариант 41
Разработал студент группы 3-78-2 Ситдиков Р.М.
Принял к.т.н., доцент кафедры ВТ Гафаров Р.М.
Ижевск 2009
Содержание
Задание………………………………………………………..……...3
Цель работы…………………………………………………...……..3
Постановка задачи…………………………………………..……….3
Анализ и разработка алгоритма……………………………..……..3
Алгоритм программы…………………………………………...…..8
Текст программы……………………………………………...……..9
Результаты моделирования программы на ЭВМ……………..….16
Вывод...………………………………………………….…………...17
Литература………………………………………………….……….18
ЛАБОРАТОРНАЯ РАБОТА №1.
ТЕХНОЛОГИЯ РАЗРАБОТКИ ПРОГРАММЫ ПРИ ОБЪЕКТНО-ОРИЕНТИРОВАННОМ ПОДХОДЕ
Задание
Разработать программную модель взаимного качения квадрата и эллипса по плоской поверхности.(рис. 1.1)

Рис. 1.1- Задание на лабораторную работу
Цель работы
Повторение и закрепление знаний в области технологии разработки ПО при объектно-ориентированном подходе на примере разработки программы моделирования взаимного качения двух объектов.
Постановка задачи
В целом задача сводится к реализации вращения квадрата и эллипса вокруг заданной оси и перемещения оси вращения.
Анализ и разработка алгоритма
В результате выполнения программы на экране должно быть следующее (рис 1.2):
 |
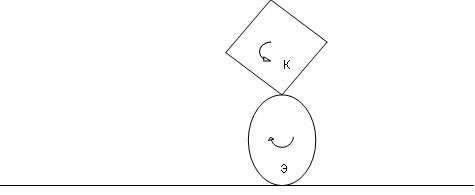
Рис. 1.2-  Постановка задачи
Постановка задачи
Здесь К – это ось вращения квадрата, а Э – ось вращения эллипса. Основными структурными элементами (объектами) этого изображения являются точки и линии, и из них могут быть построены квадрат и эллипс и скомпонована вся сцена на экране, причем эти элементы образуют следующую иерархию:
 |
Опишем эти объекты в соответствии с положениями ООП-программирования.
· Объект типа TPoint является точкой с координатами x,y вещественного типа и цветом Pcolor. Вещественный тип координат точки определяется тем, что этот объект предназначен для описания вершин квадрата и эллипса, а при вращении они могут принимать вещественные значения. Кроме очевидных необходимых методов Init, Show и Destructor добавим в их число и виртуальный метод Rotate реализующий плоское вращение точки вокруг заданной оси. Вращение точек вокруг заданной оси вращения осуществляется по формуле:
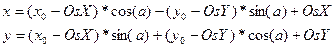 ,где х0 , у0 – начальные координаты точки; х, у – координаты после поворота; а – угол поворота; OsX, OsY – координаты оси вращения.
,где х0 , у0 – начальные координаты точки; х, у – координаты после поворота; а – угол поворота; OsX, OsY – координаты оси вращения.
Координаты оси вращения имеют вещественный тип и задаются извне (являются входными параметрами метода). Вещественные значения координат оси обусловлены тем, что длина отрезков, из которых состоит эллипс, может быть как целой, так и вещественной.
Методы TPoint достаточно простые: Constructor Init заполняет О-поля объекта; процедура Rotate, как описано выше вычисляет новые координаты точки по формулам геометрического поворота вокруг заданной оси на угол step, величина которого зависит от требуемой скорости вращения объекта и процедура Show скорее служит прототипом для дальнейшего наследования, чем для самостоятельного использования.
· Изображение эллипса может быть получено с помощью стандартной для модуля graph процедуры Ellipse, но построенный таким образом эллипс невозможно вращать, поэтому будем рассматривать его как многоугольник и строить с помощью процедур moveto и lineto по координатам вершин. Таким образом объект типа TEllipse конструируется из точек типа TPoint, количество которых определяется значением константы det, и переменной EColor для задания его цвета а его виртуальные методы Show и Rotate обеспечивают полиморфические свойства отображения и поворота. Координаты вершин вычисляются по формулам:
x=a*cos(t); y=b*sin(t), t= 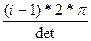
где а и b – горизонтальный и вертикальный радиусы эллипса, а t вычисляется в зависимости от номера точки i и значения константы det. Процедура инициализации располагает центр эллипса в верхнем левом углу экрана.
· Объект типа TLine наследует все поля и методы TPoint, но перекрывает своими виртуальными методами Show и Rotate соответствующие методы родителя. Кроме унаследованных полей x и y, этот тип содержит два поля pn и pk типа TPoint, которые являются объектами и описывают две точки, задающие отрезок прямой на плоскости – будущую сторону квадрата. Виртуальные методы Show и Rotate позволяют отображать этот отрезок на экране цветом Lcolor и поворачивать его вокруг заданной оси. На первый взгляд, непонятна роль унаследованных полей x и y. Тем более, что можно было в типе TLine обойтись только одним полем pn, а координаты конца отрезка поместить в x и y. Однако, такой подход привел бы к разным синтаксическим конструкциям при обращении к начальной и конечной точкам отрезка, что повлияло бы на единообразие стилистики программы и затруднило бы ее восприятие. Кроме того, потомки данного типа могут использовать эти поля для своих специфических нужд, например, помещая в них координаты середины отрезка.
· Объектный тип TSquare (квадрат) конструируется из 4-х отрезков типа ТLine, длины стороны квадрата as и переменной Scolor для задания его цвета, а виртуальные методы Show и Rotate обеспечивают его полиморфические свойства отображения и поворота. Процедура инициализации располагает квадрат в верхнем левом углу экрана.
· Тип TScreen, находясь на самом нижнем уровне иерархии, описывает самый сложный объект – экран, со всеми его «действующими лицами»: катящимся эллипсом, катящимся по поверхности эллипса квадратом и поверхностью качения. Этот тип включает в себя эллипс, унаследованный из родительского типа, объект типа TSquare, О-поля для задания положения и цвета поверхности качения (поля Gdisp и Gcolor) и соответствующий метод DrawGround ее прорисовки на экране, поля line0, sides0 для сохранения предыдущих координат эллипса и квадрата, а также поля nom, OsXЕ,OsYЕ для номера точки эллипса, являющейся текущей осью вращения квадрата и текущих координат положения оси вращения эллипса соответственно. Методы ShiftOsXY и ShiftOsXYЕ отвечают за своевременное перемещение осей вращения квадрата и эллипса при качении и являются виртуальными, поскольку в потомках может возникнуть необходимость их модификации. Метод ShiftOsXYЕ перемещает ось вращения эллипса при достижении какой-либо из его точек поверхности качения. Метод ShiftOsXY контролирует контакт эллипса со сторонами квадрата. Для определения момента входа эллипса в пределы квадрата после очередного поворота его на небольшой угол step проводятся испытания всех точек эллипса на предмет входа их в пределы кавдрата. С этой целью вычисляются координаты каждой из этих точек в локальной системе координат X10Y1квадрата. Для этого используются методы CalcABC и Dist. В методе CalcABC вычисляются параметры прямой Ax+By+C=0– одной из осей локальной системы координат X10Y1 (линии, проходящей через центры противоположных сторон квадрата) по формулам:
A=yk - yn; B := xn - xk; C := xk * yn - xn * yk,
где xn, yn, xk, yk – координаты начала и конца отрезка прямой.
В методе Dist вычисляется расстояние (координата) точки (вершины эллипса) до соответствующей оси по формуле:
|
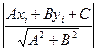 ,
, 
Если обе полученные координаты по абсолютной величине меньше половины длины стороны квадрата, то данная точка эллипса входит в пределы квадрата, поэтому ось вращения перемещается в эту вершину эллипса. Факт смены оси вращения отмечается в результате функции ShiftOsXY значением True. Метод Rotateall обеспечивает вращение квадрата и эллипса вокруг точки вращения эллипса. Метод Go реализует продвижение изображения на один кадр при срабатывании таймера и регенерацию сцены при достижении эллипсом края окна.
Алгоритм программы
























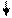


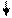
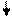
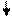






 Блок-схема основной процедуры программы TScreen.go:
Блок-схема основной процедуры программы TScreen.go:
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 |
Текст программы
program Lab;
uses
Forms,
Kurspas in 'Kurspas.pas' {Form1},
ElSq in 'ElSq.pas' {Form2};
{$R *.res}
begin
Application.Initialize;
Application.CreateForm(TForm1, Form1);
Application.Run;
end.
unit Kurspas;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, ExtCtrls, ElSq;
Const
sizeSq = 100; { размер квадрата }
colorEl = clBlue; {цвет эллипса}
colorSq = clYellow; { цвет квадрата }
colorG = ClGreen; { цвет поверхности качения }
type {описание формы}
TForm1 = class(TForm)
Image1: TImage;
Button1: TButton;
Button2: TButton;
Timer1: TTimer;
Button3: TButton;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Timer1Timer(Sender: TObject);
procedure FormResize(Sender: TObject);
procedure FormCreate(Sender: TObject);
procedure Button3Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
Var screen: TScreen; {определение объекта типа TScreen}
{$R *.dfm}
procedure TForm1.Button1Click(Sender: TObject); {при нажатии кнопки Go}
begin
timer1.Enabled:=true; {активировать таймер}
end;
procedure TForm1.Button2Click(Sender: TObject); {при нажатии кнопки Exit}
begin
screen.Done; {вызвать деструктор}
Close; {завершить выполнение приложения}
end;
procedure TForm1.Timer1Timer(Sender: TObject); {при срабатывании таймера}
begin
Screen .Go; {запустить процедуру анимации экрана}
end;
procedure TForm1.FormCreate(Sender: TObject); {при запуске приложения}
begin
Screen.Init(sizeSq, colorEl, colorSq, colorG, Image1.height-30,Image1 );
{инициализировать объект Screen}
end;
procedure TForm1.Button3Click(Sender: TObject); {при нажатии кнопки Stop}
begin
timer1.Enabled:=false; {остановить таймер}
end;
end.
unit ElSq;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ExtCtrls;
Const
det = 36; {количество вершин для построения эллипса}
xrad = 40; {горизонтальный радиус эллипса}
yrad = 25; {вертикальный радиус эллипса}
kv = 4; {количество сторон квадрата}
speed1 = 0.9; {скорость вращения эллипса}
speed = 1.5; {скорость вращения квадрата}
one = pi/180; {один градус в радинах}
step = one*speed; {шаг поворота квадрата}
step1 = one*speed1; {шаг поворота эллипса}
Type TPoint = Object {О-тип точка}
x,y :Real; {координаты точки}
Pcolor :Byte; {цвет точки}
Constructor Init ( xx,yy :Real; col :Byte );
Procedure Rotate ( xOs, yOs, spd :real ); Virtual;
Procedure Show ( col :Byte; var image1:TImage ); Virtual;
Destructor Done;
End;
TSide = array [1..det] of TPoint; {тип для описания вершин эллипса}
TEllipse=Object ( TPoint ) {О-тип эллипс}
line :TSide; {вершины эллипса}
EColor :Byte; {его цвет}
Constructor init (colE :byte);
procedure Rotate (xOsE, yOsE, spd:real); Virtual;
Procedure Show (col:Byte; var image1:TImage); Virtual;
Destructor Done;
end;
TLine = Object ( TPoint ) {О-тип отрезок}
pn, pk :TPoint; {начальная и конечная точки отрезка}
Lcolor :Byte; {его цвет}
Constructor Init ( x1,y1,x2,y2 :Real; col :Byte );
Procedure Rotate ( xOs, yOs, spd :real ); Virtual;
Procedure Show ( col :Byte; var image1:TImage ); Virtual;
Destructor Done;
End;
TSides = Array [ 0..kv-1 ] Of TLine; {тип для описания сторон квадрата}
TSquare = Object ( TLine ) {О-тип квадрат}
as :Byte; {длина стороны квадрата}
Sides :TSides; {стороны квадрата}
Scolor :Byte; {его цвет}
Constructor Init ( aa, colK :Byte );
Procedure Rotate ( xOs, yOs, spd :real ); Virtual;
Procedure Show ( col :Byte; var image1:TImage ); Virtual;
Destructor Done;
End;
TScreen = Object ( TEllipse ) {О-тип сцена}
image1 :TImage; {адрес картинки}
Elps :TEllipse; {эллипс}
Sqre :Tsquare; {квадрат}
Gdisp :Integer; {смещение поверхности качения}
Gcolor :TColor; {цвет поверхности качения}
line0 :TSide; {переменные для запоминание текущего положения фигур}
sides0 :TSides;
OsXE,OsYE,nom :Integer; {переменные для хранения координат осей вращения}
Constructor Init ( aa:Byte; colE, colK, colG :TColor; dG :Integer; var image:TImage );
Function ShiftOsXY :Boolean; Virtual;
Function ShiftOsXYE :Boolean;
Procedure CalcABC( Var S1,S2 :TLine; Var A,B,C :Real );
Function Dist( A,B,C, xx,yy :Real) :Real;
Procedure Rotateall(xOs,yOs:Integer; spd:real);
Procedure Go; Virtual;
Procedure DrawGround; Virtual;
Destructor Done;
End;
{TForm2 = class(TForm)
private }
{ Private declarations}
{ public }
{ Public declarations }
{ end;
var
Form2: TForm2;}
implementation
{---------------------------------------------------------------}
Constructor TPoint .Init ( xx, yy :Real; col :TColor );
Begin x:=xx; y:=yy; Pcolor := col; End;
Procedure TPoint .Rotate ( xOs,yOs :Integer; spd:real );
Var xx, yy :Real;
Begin xx := (x - xOs)*Cos(spd) - (y - yOs)*Sin(spd) + xOs;
yy := (x - xOs)*Sin (spd) + (y - yOs)*Cos(spd) + yOs;
x :=xx; y:=yy;
End;
Procedure TPoint .Show ;
Begin
Image1.Canvas.pixels[Round(x),Round(y)]:=col;
End;
Destructor TPoint .Done;
Begin End;
{---------------------------------------------------------------}
Constructor TLine .Init ( x1,y1,x2,y2 :Real; col :TColor );
Begin pn.Init(x1,y1,col); pk.Init(x2,y2,col); Lcolor:=col; End;
Procedure TLine .Rotate ( xOs,yOs :Integer; spd:real );
Begin pn.Rotate( xOs,yOs,spd ); pk.Rotate( xOs,yOs,spd ); End;
Procedure TLine .Show ;
Begin If col=clWhite Then image1.canvas.pen.color:= col Else image1.canvas.pen.color:= Lcolor;
image1.Canvas.MoveTo(Round(pn.x),Round(pn.y));
image1.canvas.LineTo(Round(pk.x),Round(pk.y));
End;
Destructor TLine .Done;
Begin End;
{---------------------------------------------------------------}
Constructor TEllipse.init(colE:byte); {инициализация эллипса}
var i:byte;
px,py:real;
Begin
EColor:=colE;
for i:=1 to det do begin
px:=xrad*cos((i-1)*2*pi/det); {определение координат точек}
py:=yrad*sin((i-1)*2*pi/det);
with line[i] do init(px,py,colE);
end;
end;
Procedure TEllipse.rotate(xOsE, yOsE, spd :real ); {вращение эллипса}
Var i:byte;
begin
for i:=1 to det do line[i].rotate(xOsE,yOsE,spd); {вращение каждой точки}
end; {эллипса}
procedure TEllipse.Show; {процедура отображения (стирания)}
var i:byte; {эллипса}
begin image1.Canvas.Pen.Color:=col; {установка цвета эллипса}
image1.canvas.moveto(Round(line[1].x),round(line[1].y));{помещение текущего указателя в первую вершину эллипса}
for i:=det downto 1 do
with line[i] do image1.canvas.lineto(round(x),round(y));{прорисовка эллипса по точкам}
end;
destructor TEllipse.done;
begin end;
{---------------------------------------------------------------}
Constructor TSquare .Init ( aa, colK :Byte ); {инициализация квадрата}
Begin
as := aa; {установка размера стороны квадрата}
Sides[0]. Init ( as, as, 0, as, colK ); {инициализация сторон квадрата}
Sides[1]. Init ( 0, as, 0, 0, colK );
Sides[2]. Init ( 0, 0, as, 0, colK );
Sides[3]. Init ( as, 0, as, as, colK );
Scolor := colK;
End;
Procedure TSquare .Rotate ( xOs, yOs, spd:real ); {вращение квадрата}
Var i :Byte;
Begin
For i:=0 To kv-1 Do Sides[i] .Rotate ( xOs,yOs,spd );
End;
Procedure TSquare .Show; {отображение(стирание) квадрата}
Var i :Byte;
Begin For i := 0 To kv-1 Do Sides[i].Show ( col,image1 ); End;
Destructor TSquare .Done;
Begin End;
{---------------------------------------------------------------}
Constructor TScreen .Init ( aa:Byte; colE, colK, colG :TColor; dG :Integer; var image:TImage );
Var i :Byte;
Begin
{закрашиваем экран белым}
image1:=image; {принимаем адрес нашего экрана для рисования}
image1.Canvas.Brush.Color:=clWhite;
Image1.Canvas.Brush.Style:=bsSolid;
image1.Canvas.FillRect(rect(0,0,image1.Width,image1.Height));
Sqre.Init ( aa, colK ); {инициализируем квадрат}
Elps.init(colE); {инициализируем эллипс}
Gdisp := dG;
For i := 0 To kv-1 Do With Sqre.Sides[i] Do Begin {ставим квадрат на эллипс}
pn.y := pn.y + Gdisp - Sqre.ss-2*yrad-1;
pk.y := pk.y + Gdisp - Sqre.ss-2*yrad-1;
pn.x := pn.x + xrad;
pk.x := pk.x + xrad;
End;
For i:=1 to Det do With Elps.line[i] do begin {ставим эллипс на поверхность}
y:=y+Gdisp-yrad;
x:=x+xrad; end;
Gcolor := colG; {принимаем цвет поверхности}
nom:=det-1; {устанавливаем начальные значения координат осей вращения}
OsXE:= xrad;
OsYE:= Gdisp;
DrawGround; {рисуем поверхность}
End;
Procedure TScreen .DrawGround; {процедура прорисовки поверхности}
Begin Image1.canvas.pen.color:= Gcolor; {установка цвета прорисовки прямоугольника}
Image1.Canvas.Brush.Color:=Gcolor; {и цвета заливки}
image1.Canvas.MoveTo(0, Gdisp + 1); {прорисовка линий}
Image1.canvas.LineTo( Image1.Width, Gdisp + 1 );
Image1.Canvas.Brush.Style:=bsBDiagonal; {установка стиля заливки}
Image1.canvas.FloodFill(2,Gdisp+2,Gcolor, fsBorder); {заливка поверхности}
image1.Canvas.Refresh;
End;
Function TScreen .ShiftOsXYE :Boolean; {смещение оси вращения эллипса}
var i:byte;
Begin
ShiftOsXYE := False;
for i:=1 to det do {перебираем все точки}
If elps.line[i].y>Gdisp Then {если точка оказалась ниже поверхности качения}
if Round(elps.line[i].x)>OsXE then Begin {если координата х этой точки отличается от текужей х координаты оси вращения эллипса}
elps.line:=line0; {то восстанавливаем предыдущее положение фигур}
sqre.Sides:=sides0;
OsXE := Round(elps.line[i].x); {смещаем ось вращения}
ShiftOsXYE := True; End;
End;
{следующие 2 процедуры как в методичке, принцип действия объяснен в анализе алгоритма}
Procedure TScreen.CalcABC( Var S1,S2 :TLine; Var A,B,C :Real );
Var xn,yn,xk,yk :Real;
Begin xn := (S1.pn.x+S2.pk.x)/2; yn := (S1.pn.y+S2.pk.y)/2;
xk := (S1.pk.x+S2.pn.x)/2; yk := (S1.pk.y+S2.pn.y)/2;
A := yk - yn; B := xn - xk; C := xk * yn - xn * yk;
End;
Function TScreen.Dist( A,B,C, xx,yy :Real) :Real;
Begin Dist := Abs((A*xx+B*yy+C) / Sqrt(A*A+B*B)); End;
Function TScreen.ShiftOsXY :Boolean; {смещение оси вращения квадрата}
Var Ax, Bx, Cx, Ay, By, Cy, xx, yy :Real;
i :Integer;
Begin
ShiftOsXY := False;
{подсчет параметров новой системы координат}
CalcABC( Sqre.Sides[1], Sqre.Sides[3], Ax, Bx, Cx );
CalcABC( Sqre.Sides[0], Sqre.Sides[2], Ay, By, Cy );
For i := 1 To Det Do {перебор всех точек эллипса}
Begin
yy := Dist( Ay, By, Cy, Elps.line[i].x, Elps.line[i].y ); {подсчет координат точки в новой системе координат}
xx := Dist( Ax, Bx, Cx, Elps.line[i].x, Elps.line[i].y );
If ( xx <= Sqre.ss/2 ) and ( yy <= Sqre.ss/2) {если точка внутри квадрата}
Then If i<>nom then {то если ее номер отличается от текущего номера}
Begin
nom:=i; {смещаем ось вращения}
ShiftOsXY := True;
sqre.Sides:=sides0; {восстанавливаем предыдущее положение квадрата}
Exit;
End;
End;
End;
Procedure TScreen.Rotateall(xOs,yOs:Integer; spd:real); {вращение всех фигур}
var xx,yy:real;
Begin Sqre.rotate(xOs,yOs,spd);
Elps.rotate(xOs,yOs,spd);
End;
Procedure TScreen.Go; {продвижение на 1 кадр}
Begin
Sqre.Show ( clWhite,image1 ); {стираем фигуры}
Elps.show ( clWhite,image1 );
sides0:=sqre.Sides; {запоминаем положение квадрата}
repeat
sqre.Rotate ( Round(elps.line[nom].x), Round(elps.line[nom].y), step ); {вращаем квадрат}
until not ShiftOsXY; {пока вращение не пройдет без необходимости сместить ось вращения}
sides0:=sqre.Sides; {запоминаем положение обеих фигур}
line0:=elps.line;
Repeat
Rotateall( OsXE, OsYE, step1 ); {вращаем обе фигуры}
until not ShiftOsXYE; {пока вращение не пройдет без смещения оси вращения}
Sqre.Show ( Sqre.Scolor, Image1 ); {прорисовываем фигуры}
Elps.Show (Elps.Ecolor,image1); image1.Refresh;
If OsXE > Image1.Width then {если дошли до края окна, то инициализируем сцену заново}
Init ( Sqre.ss, Elps.Ecolor, Sqre.Scolor, Gcolor, Gdisp,image1 );
{Until False;}
End;
Destructor TScreen.Done;
Begin End;
{---------------------------------------------------------------}
end.
