Разрешение коллизий методом открытой адресации.

Другой путь решения проблемы, связанной с коллизиями, состоит в том, чтобы полностью отказаться от ссылок, и просматривать различные записи таблицы одну за одной до тех пор, пока не будет найден ключ К или пустая позиция. Идея заключается в формулировании правила, согласно которому по данному ключу К определяется "пробная последовательность", т.е. последовательность позиций таблицы, которые должны быть просмотрены при вставке или поиске К. Если при поиске К согласно определенной этим ключом последовательности встречается пустая позиция, можно сделать вывод о том, что К в таблице отсутствует. Этот общий класс методов назван открытой адресацией.

Простейшая схема открытой адресации, известная как линейное исследование использует циклическую последовательность проверок

h(K), h(K) - 1, ..., 0, М - 1, М - 2, ..., h(K) + 1

Ниже на рисунке 31 приведен пример распределения ключей в хеш таблицы, если исходными данными были ключи:K=EN, TO, TRE, FIRE, FEM, SEEK, SYV с хеш кодами 2, 7, 1, 8, 2, 8, 1

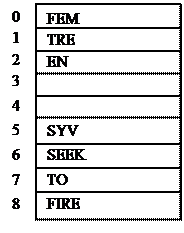Рис. 31. Линейная хеш-адресация

Данный алгоритм хорошо работает в начале заполнения таблицы, однако по мере заполнения процесс замедляется, а длинные серии проб становятся все более частыми. Так, среднее количество проб, требуемое данным методом составляет:

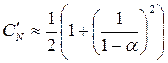(неудачный поиск)

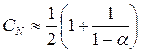(удачный поиск)

где a=N/M – коэффициент заполненности таблицы

Одним из способов защиты от последовательных хеш-кодов состоит в установке способа обхода элементов не по одному, т.е. i:=i-1, а сразу на несколько шагов: i:=i-C. Можно использовать любое положительное значение C, взаимно простое с M, поскольку последовательность проб в этом случае будет проверять в конечном счете все позиции таблицы без исключения. Такое изменение немного замедлит работу программы.

Хотя фиксированное значение C не приводит к устранению длинных серий проб, можно существенно улучшить ситуацию, сделав C зависящим от К. Эта идея позволяет выполнить важную модификацию алгоритма.

Данная модификация называется открытая адресация с двойным хешированием. Этот алгоритм почти идентичен предыдущему алгоритму, но проверяет таблицу немного иначе, используя две хеш-функции: h₁(K) и h₂(K). Как обычно, значения h₁(K) находятся в диапазоне от 0 до М - 1 включительно; функция h₂(K) должна порождать значения от 1 до М - 1, взаимно простые с М. Сравнение проб осуществляется путем сдвига переменной, отвечающей за текущий сдвиг на значение h₂(K).

Для вычисления h₂(K) было предложено несколько различных вариантов. Если М - простое число и h₁(K) = K mod M, можно положить h₂(K)=1+(K mod (М - 1)); однако, поскольку М-1 четно, можно положить h₂(K) = 1 + (К mod (М - 2)). Кроме того, можно взять в качестве h₂(K) величину 1+([К/М] mod (М - 2)) в связи с тем, что частное [К/М] может быть получено в регистре как побочный результат вычисления h₁(K).

Если М=2^m и используется мультипликативное хеширование, то h₂(K) может быть вычислена методом простого сдвига на m дополнительных битов влево с выполнением операции "ИЛИ" с 1. Эти операции выполняются быстрее метода деления.

Можно также допустить зависимость h₂(K) от h₁(K), как было предложено Гари Кноттом, например, при простом М можно положить

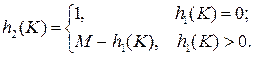
Этот метод выполняется быстрее повторного деления, однако он вызывает определенную вторичную кластеризацию, что приводит к небольшому увеличению числа проб из-за повышения вероятности того, что два или несколько ключей пойдут одному и тому же пути.

Для приведенной выше формулы вычислены средние значения проб при неудачном и удачном поисках:

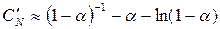(неудачный поиск)

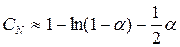(удачный поиск)

4. Сетевые алгоритмы [22]

Сеть, или граф - это набор узлов, связанных ребрами, или дугами. В отличие от дерева, в сети нет предков и потомков. Узлы, соединенные с другими узлами, являются скорее соседями, чем родительскими или дочерними узлами.

Каждое звено в сети может иметь соответствующее направление. В этом случае сеть называется направленной сетью. Каждая дуга может также иметь соответствующую стоимость. В сети улиц, например, стоимость равна времени, которое требуется, чтобы проехать по участку дороги, представленному дугой сети. На рис. 32 показана небольшая направленная сеть, в которой числа рядом с дугами соответствуют их стоимости.

Рис. 32. Направленная сеть со стоимостью связей

Путь между узлами А и В - это последовательность дуг, которые соединяют эти узлы. Если между любыми двумя узлами сети есть не больше одного ребра, то путь можно описать, перечислив входящие в него узлы. Поскольку такое описание проще представить наглядно, пути по возможности описываются именно так. На рис. 32 путь, содержащий узлы В, Е, F, G, Е, и D, соединяет узлы В и D.

Цикл - это путь, который соединяет узел с самим собой. Путь Е, F, G, E на рис. 32 является циклом.

Путь называется простым, если он не содержит циклов. Путь В, Е, F, G, Е, D не является простым, потому что он содержит цикл Е, F, G, E.

Если между двумя узлами существует какой-либо путь, то должен существовать и простой путь между ними. Его можно найти, удалив все циклы из первоначального пути. Например, если заменить цикл Е, F, G, Е узлом Е в пути В, Е, F, G, Е, D, получится простой путь В, Е, D между узлами В и D.

Сеть называется связанной, если между любыми двумя узлами сети есть хотя бы один путь. В направленной сети не всегда очевидно, существует такая связь или нет. На рис. 33 сеть слева связана. Сеть справа не является таковой, потому что от узла Е к узлу С нет ни одного пути.

Рис. 33. Пример связанной и несвязанной сети

Представления сетей

Для представления сетей можно использовать большинство представлений, которые использовались для деревьев. Например, для сохранения сетей могут использоваться такие представления, как метод полных узлов, списки дочерних узлов (для сетей список соседних узлов) и представление нумерацией связей.

Для разных приложений лучше подходят разные представления сети. Представление полными узлами приводит к хорошим результатам, если каждый узел сети связан с ограниченным числом ребер. Список соседних узлов обеспечивает большую гибкость, чем метод полных узлов. Представление с помощью нумерации связей, хотя его сложнее изменять, требует меньше памяти для сохранения сети. Кроме того, несколько вариантов представления ребер могут упростить управление определенными типами сетей. Эти форматы используют один класс для представления узлов и другой - для представления связей. Применение класса для связей облегчает работу со свойствами ребра, такими как стоимость.

Например, направленная сеть со стоимостью ребер может использовать следующее определение для класса узла и дуги. Каждое ребро хранит указатели на узлы, где оно начинается и заканчивается. Каждый узел хранит связанный список ребер, исходящих из него. Узел также имеет указатель NextNode, и программа может сохранять все узлы сети в связанном списке.

type

PLink=^TLink;

PNode=^TNode;

TLink=record

ToNode:PNode; // Конечный узел звена

Cost:integer; // Стоимость

NextLink:PLink; // Следующее звено в списке звеньев начального узла

end;

TNode=record

ID:integer; // Идентификатор узла

LinkSentinel:TLink; // Звенья, исходящие из данного узла

NextNode:PNode; // Следующий узел в списке узлов

end;

Классы узла и дуги часто расширяют для удобства работы с конкретными алгоритмами. Например, к классу узла часто добавляется логическое поле Marked. Когда программа обращается к узлу, она устанавливает Marked в True, чтобы впоследствии легко можно было его отыскать.

Для ненаправленной сети используется несколько другое представление. Класс узла остается таким же, а вот класс дуги включает указатели на оба соединяемых узла, которые на каждом конце ребра могут указывать на одну и ту же его структуру.

type

TLink=record

Node1: PNode; // Узел на одном конце дуги

Node2: PNode; // Узел на другом конце

Cost:integer; // Стоимость

NextLink:PLink; // Следующее звено в списке звеньев начального узла

end;