Раздел 2. Современная теория информации

Глава 3. Обработка информации

Адаптивная АСУП

Поскольку извлечение данных происходит, как правило, когда известны структура и применяемый математический аппарат, то дальнейшее изложение сути этапов (рис. 1.9) целесообразно было бы проводить в таком порядке: обработка информации; хранение информации; извлечение информации; отображение и использование информации.

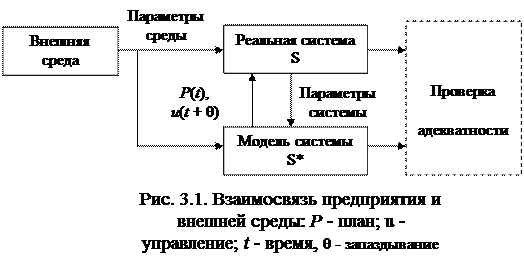Среда и цели работы системы. Работа автоматизированной системы управления в значительной мере определяется средой (рис. 3.1).

В современных рыночных условиях среда характеризуется изменениями спроса, ресурсного обеспечения, цены. Превалирующую роль играют изменения спроса. Возможны два варианта изменения (рис. 3.2).

1. Быстрое количественное изменение спроса на старую продукцию (в том числе - внеочередные выгодные для предприятия заказы).

Рис. 3.2. Процедура ежедневного перехода на выпуск новой (Р4) продукции и одновременного снятия старой (Р3) продукции: 1, 2 – мгновенное и постепенное полное снятие старой продукции; 3, 4 - мгновенное и постепенное частичное снятие старой продукции; 5, 6; 7, 8 – мгновенная и постепенная постановка на выпуск новой продукции во время и после снятия старой продукции; 9 – постепенная постановка на выпуск новой продукции после снятия старой (через время запаздывания Т_З).

Математически такой спрос R(t) отображается выражением

R₃(t) = R₃^с(t) + DR₃ 1(t - q), (3.1)

где R₃^с(t) – вектор-столбец прежнего спроса; DR₃ – вектор-столбец количественног изменения спроса; q - момент изменения спроса; t - время; 1(q) – единичная функция.

2. Появление быстро изменяющегося спроса на новую продукцию (рис. 3.2)

R₄(t) = R₄*1(t - q), (3.2)

где R₄(t) – вектор-столбец спроса на новую продукцию вида; q – момент изменения спроса. В дальнейшем, не снижая общности, будем полагать q = 0.

Быстрое изменение спроса приводит к необходимости приспособления производителя к потребителю (системы, настраиваемые на потребителя), поиску конкурентоспособных решений прежде всего путем уменьшения инерционности производства при одновременном повышении качества продукции, оперативным переходом на выпуск новой продукции.

Целью адаптивных автоматизированных систем управления производством является быстрая реакция на изменения состава вектора спроса при оперативном переходе на выпуск новой продукции путем изменения структуры систем.

Структура. Автоматизированные системы имеют два представления структуры: подсистемное и процедурное.

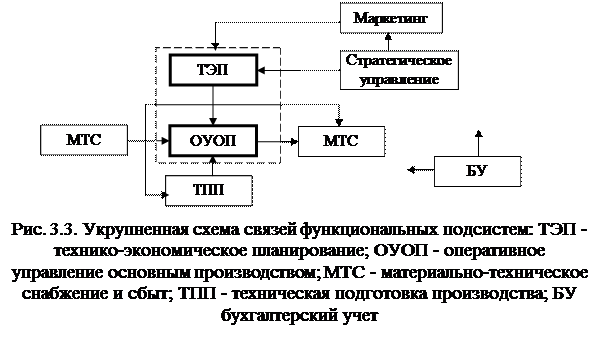
При подсистемном представлении (рис. 3.3) структурным элементом служит функциональная подсистема.

Подсистема – часть системы, выделенная по неформальному признаку.

Составной частью функциональной подсистемы является задача АСУП.

1. Быстрое количественное изменение спроса на старую продукцию (в том числе - внеочередные выгодные для предприятия заказы).

Задача АСУП – часть алгоритма функциональной подсистемы и рассматриваемая относительно самостоятельно.

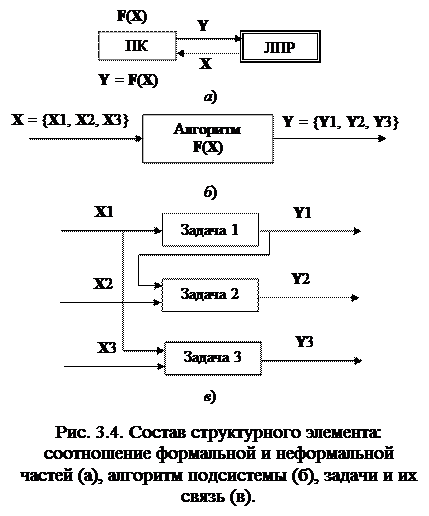
В любом структурном элементе (функциональной подсистеме) возможно выделить (рис. 3.4, а) формальную часть (персональный компьютер) и неформальную часть (ЛПР).

Формальная часть подсистемы может быть описана некоторым укрупненным векторным алгоритмом Y = F(X) – где Y и X - векторы входных и выходных данных, F(X) – функция (алгоритм) преобразования структурного элемента. Алгоритм – правило преобразования входной информации в выходную (рис. 3.4, б).

Размерности векторов X и Y значительны в любом элементе. Реализация, равно как и использование в процессе эксплуатации автоматизированной системы такого алгоритма неудобны. В связи с этим алгоритм F структурного элемента делят на связанные части, которые носят название задач АСУП (рис. 3.4, в).

Тогда вместо Y = F(X)можно записать без учета обратных связей

Y1		f11 f12 f13		X1
Y2	=	f21 f22 f23		X2
Y3		f31 f32 f33		X3

Иначе задача АСУП записывается в виде

Yi = (f_i1 f_i2 f_i3) (X₁ X₂ X₃)^T.

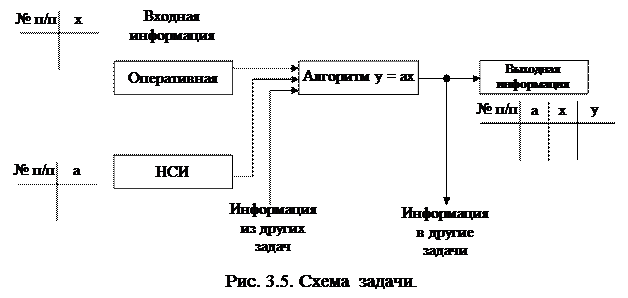
В свою очередь каждую задачу можно представить в виде, показанном на рис. 3.5, где НСИ – нормативно-справочная информация.

Как нетрудно заметить, схема подсистемы (рис. 3.4) и отдельной задачи (рис. 3.5) могут быть представлены в виде информационного цикла (рис. 1.9).

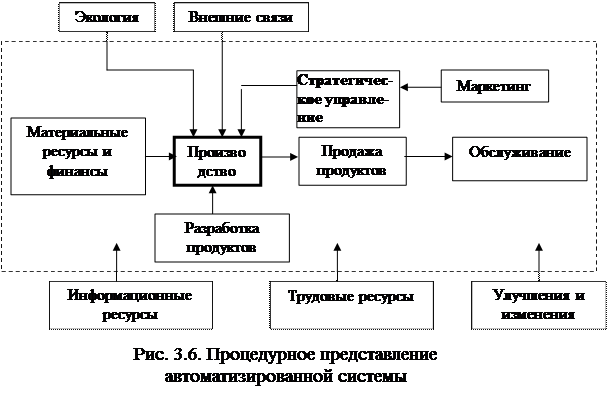
Процедурное представление автоматизированной системы показано на рис. 3.6.

В качестве структурных элементов выступают бизнес-процессы Бизнес-процесс – процесс, добавляющий стоимость.

Составной частью бизнес-процесса является бизнес-функция. Бизнес-функция – набор элементарных предписаний, которые могут быть привязаны ко времени или иметь другие условия запуска. Для компьютера – это программа, для человека – инструкция.

Далее будем оперировать бизнес-функциями применительно к компьютерам.

Независимо от используемого представления структура для частей, выделенных на рис. 3.3 (подсистемы ТЭП и ОУОП) и рис. 3.6 (бизнес-процесс «Производство»), может быть представлена в виде совокупности связанных элементов с простейшей структурой (рис. 3.7).

Процессы планирования и управления в каждом структурном элементе выделены на основе цикла управления (рис. 1.4).

Такую трехуровневую структуру назовем базовой. Она при переходе с уровня на уровень учитывает все возможные изменения по координатам и времени.

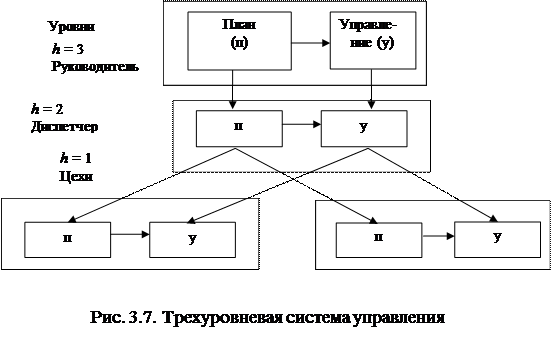Уровни h = 1 (начальники цехов) и h = 2 (диспетчер) имеют одинаковый масштаб (отсчет) по времени t_i = iv, i = 1, N, где v – элементарный интервал времени, N – количество интервалов. В то же время на уровне диспетчера увеличивается масштаб по координатам по сравнению с уровнем h = 1. На уровне h = 3 (руководство) происходит агрегация по координатам и времени T = Nv.

Математическое описание. В математическом представлении имеются связанные процессы планирования и управления, описываемые однородным методом, базирующемся на задаче динамического линейного программирования (ДЛП). В каждом из процессов выделим описания:

1) отдельного структурного элемента без учета специфики уровней;

2) отдельных элементов с учетом особенностей уровней;

3) взаимодействия элементов.

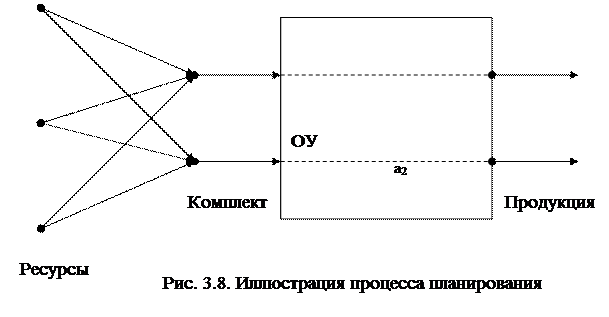
1. Отдельный элемент. Для процесса планирования описание имеет следующий вид (рис. 3.8).

P(T) ³ R(T), (3.3)

P(t_i) = P(t_i-1) - p(t_i), (3.4)

z(t_i) = Az(t_i-1) + Bp₁(t_i-1), z(0) = z₀,

i = 1, N, t_i = iv, t₀ = 0, T = Nv, (3.5)

p(t_i) = Cz(t_i), (3.6)

Dp₁(t_i) £ b(t_i-1), (3.7)

G = - FP(T)> à min, (3.8)

где z, p, P – вектор-столбцы незавершенного производства, планы текущего и с накоплением; p₁ – вектор-столбец запуска комплекта материалов в производство; R – вектор-столбец спроса; D – матрица норм расходов; b – вектор-столбец наличного количества ресурсов; F – вектор-строка прибыли от выпуска единицы продукции, A, B, C - матрицы соответствующих размерностей; T, v- интервалы времени; T = Nv.

Под комплектом понимается набор ресурсов в натуральном измерении, необходимых для выпуска единицы продукции.

Если процесс планирования статический, то используются выражения (3.3), (3.7), (3.8) задачи статического линейного программирования (СЛП).

Процесс управления получает такое описание.

Объект управления системы может быть представлен как

z(t_i) = Az(t_i-1) + Bu(t_i-1), (3.9)

y(t_i) = Cz(t_i), (3.10)

Du(t_i) £ b(t_i-1), (3.11)

где p, z, u, y, b– вектор-столбцы плана, состояния, управления размерности ресурсов, выхода, наличных ресурсов, поступления ресурсов; A, B, C – матрицы, характеризующие динамику; D- матрица норм расхода ресурсов.

Управляющая часть

e(t_i) = p(t_i) – y(t_i), (3.12)

_N

J = S{C₁e(t_i) + C₂u(t_i)} à min, (3.13)

^{i =0}

где С₁, С₂ – вектор-строки стоимостей потерь за счет отклонения от плана и потребностей в дополнительных ресурсах для управления; e(t) = p(t) – y(t) вектор отклонений; T, v- интервалы времени; T = Nv.

2. Учет особенностей уровней.

Процесс планирования. Для уровня h = 3 справедливо

z(t_i) = z(t_i-1) + [t](p₁(t_i-1) – p(t_i-1)), z (0) = z₀, (3.14)

p(t_i) = Cz(t_i-1), (3.15)

P(t_i) = P(t_i-1) + p(t_i), P(0) = 0, (3.16)

Dp₁(t_i) £ b(t_i-1), (3.17)

P(T) ³ R(T), (3.18)

b⁽¹⁾(t_i) = b⁽¹⁾( t_i-1) + Db⁽¹⁾(t_i) - A⁽¹⁾p₁(t_i), (3.19)

b⁽²⁾(t) = b⁽²⁾( t_i-1) + Db⁽²⁾(t_i), (3.20)

J = ­ C₃P(T) à min, (3.21)

где z, p – вектор-столбцы незавершенного производства и ежедневного плана; p₁ – вектор-столбец запуска комплекта материалов в производство; D – матрица норм расходов, R – вектор-столбец спроса; b – вектор-столбец наличного количества ресурсов; Db - вектор-столбец поступления ресурсов; m, y ­ материальные и другие виды ресурсов.

Для уровня h = 1 описание процесса планирования состоит из статической

D_k⁽²⁾p_1k(t_i) £ b_k⁽²⁾(t_{i - 1}),

D_k⁽¹⁾p_1k(t_i) £ b_k⁽¹⁾(t_{i - 1}),

_I

SD_k⁽¹⁾p₁₁(t_i) £ b⁽¹⁾(0), (3.22)

^{i = 1}

_I

Sp_K(t_i) £ P(T),

^{i = 1}

_I

G_k = SF_kp_k (t_i) à max

^{i = 1}

и динамической частей

z_k(t_i) = z_k(t_i-1) + [t](p_1k[t_i] – p_k[t_i]), z_k(0) = z_k0, (3.23)

p_k[t_i] = F_kz_k(t_i-1), (3.24)

P_k(t_i) = P_k(t_i-1) + p_k[t_i], P_k(0) = 0, (3.25)

b_k⁽¹⁾(t_i) = b_k⁽¹⁾(t_i-1) + Db_k⁽¹⁾[t_i] - D_k⁽¹⁾p_1k[t_i], (3.26)

b⁽²⁾_k(t) = b_k⁽²⁾(t_i-1) + Db_k⁽²⁾( t_i-1), (3.27)

где ⁽¹⁾ – индекс материальных ресурсов; ⁽²⁾ - индекс прочих ресурсов; i = 1, I – моменты времени; k = 1, K – номер подразделения.

Для уровня h = 2 вторая и последняя строки в выражении (3.22) трансформируются:

_{I I}

SD_k⁽¹⁾p_k(t_i) £ Sp_k-1(t_{i - 1}),

^{i = 1 i = 1}

_K

G = SG_k à max.

^{k= 1}

Процесс управления. Для уровня h = 3 справедливы выражения.

Объект управления системы может быть представлен как

z(t_i) = Az(t_i-1) + Bu(t_i-1), (3.28)

y(t_i) = Cz(t_i), (3.29)

Du(t_i) £ b(t_i-1), (3.30)

Y(t_i) = Y(t_i-1) + y(t_i), Y(0) = 0, (3.31)

Y(T) ³ P(T), (3.32)

b⁽¹⁾(t_i) = b⁽¹⁾( t_i-1) + Db⁽¹⁾(t_i) - A⁽¹⁾u(t_i), (3.33)

b⁽²⁾(t) = b⁽²⁾( t_i-1) + Db⁽²⁾(t_i), (3.34)

где p, z, u, y, b– вектор-столбцы плана, состояния, управления размерности ресурсов, выхода, наличных ресурсов, поступления ресурсов; A, B, C – матрицы, характеризующие динамику; D- матрица норм расхода ресурсов; ⁽¹⁾, ⁽²⁾ ­ материальные и другие виды ресурсов.

Управляющая часть

e(t_i) = p(t_i) – y(t_i), (3.35)

_N

J = S{C₁e(t_i) + C₂u(t_i)} à min, (3.36)

^{i =0}

где С₁, С₂ – вектор-строки стоимостей потерь за счет отклонения от плана и потребностей в дополнительных ресурсах для управления; e(t) = p(t) – y(t) – вектор-столбец отклонений; T, v- интервалы времени; T = Nv.

Для уровня h = 1 описание процесса управления состоит из статической

D_k⁽²⁾u_k(t_i) £ b_k⁽²⁾(t_{i - 1}),

D_k⁽¹⁾u_k(t_i) £ b_k⁽¹⁾(t_{i - 1}),

_I

SD_k⁽¹⁾u₁(t_i) £ b⁽¹⁾(0), (3.37)

^{i = 1}

_I

Su_K(t_i) £ P(T),

^{i = 1}

_I

J = S{C_1ke_k(t_i) + C_2ku_k(t_i)} à min

^{i = 1}

и динамической частей

z_k(t_i) = z_k(t_i-1) + [t](u_k[t_i] – y_k[t_i]), z_k(0) = z_k0, (3.38)

y_k[t_i] = F_kz_k(t_i-1), (3.39)

Y_k(t_i) = Y_k(t_i-1) + y_k[t_i], Y_k(0) = 0, (3.40

b_k⁽¹⁾(t_i) = b_k⁽¹⁾(t_i-1) + Db_k⁽¹⁾[t_i] - D_k⁽¹⁾u_k[t_i], (3.41)

b⁽²⁾_k(t) = b_k⁽²⁾(t_i-1) + Db_k⁽²⁾( t_i-1), (3.42)

где ⁽¹⁾ – индекс материальных ресурсов; ⁽²⁾ - индекс прочих ресурсов; i = 1, I – моменты времени; k = 1, K – номер подразделения.

Для уровня h = 2 вторая и последняя строки в выражении (3.37) трансформируются:

_{I I}

SD_k⁽¹⁾u_k(t_i) £ Sy_k-1⁽¹⁾(t_{i - 1}),

^{i = 1 i = 1}

_K

J = SJ_k à min.

^{k= 1}

3. Взаимодействие элементов. Взаимодействие в процессе планирования связано с экономическими свойствами (целесообразность оперативного перехода на выпуск новой продукции, согласование экономических интересов).

Решение проблем перехода и согласования экономических интересов удобнее показать на задачах СЛП. Для этого представленные ранее задачи ДЛП следует преобразовать в задачи СЛП.

Рассмотрим решение для общей задачи ДЛП выражений (3.3) – (3.8) и одновременно уровня h =3.

Задачи динамического линейного программирования вида (3.3) – (3.8) могут быть сведены к задаче статического линейного программирования, если для P(T) из выражения (3.4) использовать выражения (3.5) –(3.6). Тогда получим

P(T) = a₀z(0) + a₁p₁(0) + a₂p₁(1) + … + a_N-₁p₁(N-2) + a_Np₁(N-1), (3.43)

где

_{N N - s}

a₀ = СSAⁱ_, a_s = СSAⁱB,s = 1, N . (3.44)

^{i = 1 i = 0}

Тогда задача (3.3) – (3.8) получает вид

P(T) ³ R(T), (3.45)

P(t_i) = P(t_i-1) + p(t_i), P(0) = 0, (3.46)

Dp(t_i) £ b(t_i-1), (3.47)

G = - FP(T) à min. (3.48)

Можно приступить к решению проблем взаимодействия в процессе планировании.

Пусть в выражении (3.45) новая продукцияобозначена черезP₄[t] с ее прибылью - С₄ , а старая продукция–черезP₃[t] и С₃ соответственно.

Тогда простейшим условием целесообразности перехода на выпуск новой продукции является

_{I I}

SP₃(t_i) £ SP₄(t_i).

^{i = 1 i = 1}

Теперь можно приступить к проблеме согласования экономических интересов структурных элементов. Интересы проявляются через целевые функции.

Речь пойдет о согласовании задач СЛП по вертикали и по горизонтали трехуровневой структуры.

В общем случае две задачи СЛП согласованы, если

1) области ограничений совпадают или одна из них входит в другую;

2) целевые функции имеют одинаковые тенденции при одинаковом направлении изменения решения.

Начнем со специфического согласования по горизонтали в виде следующего алгоритма.

Шаг 1. Задача вида (3.45) – (3.48) решается от конечных элементов к начальным (от k = K до k = 1). Получаются оптимальные значения планов p_k^(1)*, G_k^(1)*.

Шаг 2. Задача (3.45) – (3.48) решается от начальных элементов к конечным (от k = 1 до k = K). Получаются оптимальные значения планов p_k^(2)*, G_k^(2)*.

Шаг 3. Определяется разница DG_k = G_k^(1)* - G_k^(2)*.

Шаг 4. Очевидно, что при плане p⁽²⁾_k потери несут элементы k = n + 1, K и система в целом, при плане p⁽¹⁾_k потери характерны для элементов k = 1, n.

Реальным считается направление шага 1, поскольку требуется выполнить план. Можно, не снижая общности, считать, что для элементов k = 1, n величина DG_k < 0, а для элементов k = n +1, K (n, n + 1 Î 1, K) ­ DG_k > 0.

Шаг 5. Тогда в интересах системы в целом целесообразно дополнительный выигрыш

_K

SDG_r

^{r = n + 1}

при плане p⁽¹⁾_k перераспределить.

Для этого возможно использовать метод равновесия по Нэшу или многокритериальную задачу СЛП.

Перейдем к решению задач вертикального согласования.

Уровни h = 1и h = 2 согласованы, поскольку область ограничения уровня h = 1 входит в область ограничений уровня h = 2, а тенденции изменения целевых функций совпадают.

Легко показать, что перечисленные условия справедливы для уровней h = 2и h = 3, т.е. они согласованы.

Взаимодействие в процессе управления связано с согласованием экономических свойств и координацией управленческих свойств (неколебательность переходного процесса, ковариантность по входному сигналу).

Согласование экономических интересов в процессе управления осуществляется аналогично процессу планирования.

Сложнее с координацией управленческих свойств процесса управления. В силу его многогранности нельзя определить одно свойство для координации. Требуется несколько свойств (векторное свойство).

В качестве такого векторного свойства можно взять неколебательность переходного процесса и ковариантность по входу (нулевая или минимальная установившаяся ошибка).

В системах автоматического управления нулевая ошибка на скачок входного сигнала обеспечивается введением в систему интегрирующего звена, играющего роль элемента памяти.

В организационно-экономических системах такое звено сформировать проблематично. Еще сложнее выявить аналитические условия неколебательности переходного процесса.

В связи с этим решение этих задач проводится с помощью компьютерного моделирования.

Система приема на работу

Среда и цели работы системы. Рассматриваемая система относится к одному из классов систем искусственного интеллекта - экспертным системам реального времени (ЭСРВ).

Экспертная система реального времени – вычислительная система, использующая знания эксперта, процедуры логического вывода, позволяющая дать объяснения полученным результатам и учитывающая время в явном виде. Синонимом ЭСРВ является термин «система, базирующаяся на знаниях».

Целью рассматриваемой прикладной системы является выработка кадровых решений-советов при приеме на работу по анкетным данным.

Система предназначена в помощь руководителям.

Структура. В общем случае структура такой системы может быть представлена так, как показано на рис. 3.9.

Такие ЭС могут быть использованы как элементы управляющей части системы управления.

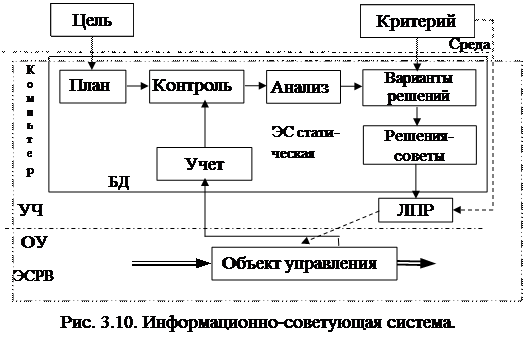
Место таких систем в цикле управления показано на рис. 3.10.

Экспертная система без блока «база правил» называется оболочкой ЭС (аналог СУБД).

На основе данных БД, правил БП в машине логического вывода вырабатывается решение-совет.

Данные могут быть и введены пользователем в режиме диалога. При необходимости ЭСРВ может дать объяснение относительно полученного результата.

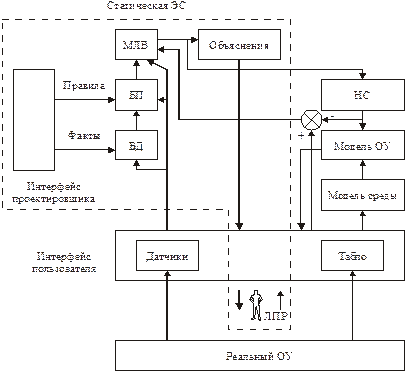
Рис. 3.9. Современная экспертная система реального времени:

БП - база правил, МЛВ - машина логического вывода (дискретная

составляющая описания управляющей части), НС - непрерывная

составляющая описания управляющей части.

ЭСРВ позволяют учесть, сохранить и провести анализ изменяющихся во времени данных, поступающих от внешних источников; работать с асинхронными процессами; обеспечить механизм рассуждений при ограниченных ресурсах; обеспечить прогноз последствий принимаемых решений-советов; обеспечить создание и поддержку интерфейсов пользователей, уровень их защиты для различных категорий пользователей.

Следует отметить, что первоначально ЭСРВ работала с моделью объекта управления (рис. 3.9). В настоящее время в ЭСРВ включают реальный объект управления, информация о состоянии которого поставляется системой датчиков и отражается на табло.

В рассматриваемой далее прикладной системе датчики и табло не используются.

Математическое описание.В рамках теории ЭСРВ решены следующие основные проблемы.