Кодирование по Шеннону-Фано

Построение кода Шеннона - Фано для источника сообщений х₁, х₂, х₃, х₄. Использование равномерного кода для этих сообщений не позволяет обеспечить максимальную скорость передачи информации. С помощью кода Шеннона - Фано рассматриваемые сообщения можно передать с максимальной скоростью, равной пропускной способности двоичного канала. Кодирование сообщений в этом случае иллюстрируется табл. 1, которая составлена следующим образом.

Записывают сообщения в порядке убывания их вероятностей.

Проводят первое деление всех сообщений на две подгруппы I и II так, чтобы сумма вероятностей сообщений в подгруппах I и II была бы по возможности одинаковой. В данном случае это условие выполняется точно: при первом делении в подгруппу I входит сообщение х₁, вероятность которого равна 0,5, а в подгруппу II входят сообщения х₂, х₃, х₄, сумма вероятностей которых (0,25+0,125+0,125) будет тоже составлять 0,5.

Проводят второе аналогичное деление для каждой из полученных подгрупп сообщений. Процесс последовательных делений сообщений на подгруппы I и II прекращается в том случае, когда в подгруппе останется по одному сообщению.

Номер подгруппы, в которую попадает данное сообщение при каждом делении, определяет символ на соответствующей позиции кода этого сообщения. В рассматриваемой таблице принадлежность к подгруппе I обозначается символом 0, а к подгруппе II – символом 1. Так, в частности, первое деление дало на первой позиции кода для сообщения x₁ символ 0, а для остальных сообщений – символ 1.

Таблица 1

Сообще-ние xi	Вероят- ность р(хi)	Номер деления на подгруппы	Символ кода	Длительность кодовой комбинации ti
Позиции
х1	0,5		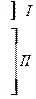		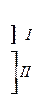		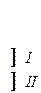	1t
х2	0,25				2t
х3	0,125				3t
х4	0,125				3t

Как следует из табл. 1, полученный код является неравномерным, т.е. сигналы разных сообщений имеют различное число символов, следовательно, разную длительность. Для наглядности в табл. 2 для сообщений х₁, х₂, х₃, х₄ приведены неравномерный код Шеннона - Фано и равномерный. Анализируя неравномерный код Шеннона - Фано, можно убедиться в том, что наиболее вероятному сообщению соответствует самая короткая кодовая комбинация, наименее вероятному – длинная. Этим можно объяснить увеличение скорости передачи информации при использовании данного кода.

Таблица 2

Сообщение xi	Код Шеннона - Фано	Равномерный код
x1
x2
x3
x4

Код Шеннона - Фано обладает еще одним существенным свойством: позволяет декодировать сообщения без введения дополнительных разделительных символов между кодовыми комбинациями, приводящих к снижению скорости передачи информации. Действительно, в рассмотренном примере короткие комбинации не совпадают с началом других более длинных кодовых комбинаций. Поэтому возможно однозначное декодирование последовательности кодовых комбинаций, формируемых непрерывно без применения разделительных символов. Коды, удовлетворяющие рассмотренному условию, называются префиксными кодами.

Практическая часть

Номер варианта	Задание
	51 53 55 57 56 56 54 54 54 52 52 52 52 56 56 57 55 51 52 53 54