Список переменного размера

Министерство общего и профессионального образования Российской Федерации

Самарский государственный университет

Кафедра БЕЗОПАСНОСТИ ИНФОРМАЦИОННЫХ СИСТЕМ

МЕТОДЫ ПРОГРАММИРОВАНИЯ. КЛАССИЧЕСКИЕ АЛГОРИТМЫ

Учебно-методическое пособие для студентов

механико-математического факультета

специальности 075200 – Компьютерная безопасность

Издательство «Самарский университет»

2004 г.

Сост. А.Н. Крутов. Методы программирования. Классические алгоритмы: Учебно-методическое пособие. – Самара: Изд-во «Самарский университет», 2004. – 77 с.

Основой данного пособия являются материалы лекций, прочитанных автором по первой половине курса “Методы программирования” для специальности 075200 – Компьютерная безопасность.

В пособии кратко рассматриваются наиболее распространенные в настоящее алгоритмы по обработки информации.

Учебно-методическое пособие предназначено для студентов механико-математического факультета Самарского государственного университета (специальность «Компьютерная безопасность»).

Рецензенты:

Рогачева Е.В., доцент кафедры информатики и высшей математики

Ефимов Ю.Е., доцент кафедры информатики и высшей математики

Содержание

Введение.. 4

1. Структуры данных.. 5

1.1 Треугольные массивы 7

1.2 Списки 8

1.3 Стеки 13

1.4 Очереди. Деки. 14

1.5 Деревья 15

2. Сортировка.. 33

2.1 Внутренняя сортировка 33

2.2 Внешняя сортировка 44

3. Поиск.. 45

3.1 Последовательный поиск 46

3.2 Поиск путем сравнения ключей. 48

3.3 Хеширование 49

4. Сетевые алгоритмы 54

4.1 Представления сетей. 55

4.2 Обход сети. 57

4.3 Наименьший каркас дерева. 59

4.4 Кратчайший путь. 60

5. Задачи для лабораторных работ.. 74

Заключение.. 76

Библиографический список.. 77

Введение

В настоящее время компьютерная техника развивается стремительными темпами. Однако ключевая роль в достижении успеха большинства компьютеризованных систем принадлежит не используемому оборудованию, а программному обеспечению. Поэтому задача разработки качественных и надежных программных продуктов с использованием оптимальных алгоритмов никогда не перестанет быть актуальной. Настоящее пособие является первой частью цикла учебных пособий по курсу “Методы программирования” для специальности 075200 – Компьютерная безопасность. Данное пособие посвящено описанию алгоритмов, ставших уже классическими, несмотря на относительно небольшую историю развития информатики и программирования.

В первой главе настоящего пособия описываются основные структуры данных, применяемые в программировании. К ним относятся массивы, списки, стеки, очереди, а также деревья. Вторая глава посвящена описанию алгоритмов сортировки. В начале описываются алгоритмы внутренней сортировки, когда весь сортируемый массив данных считывается в оперативную память. Далее приводятся алгоритмы внешней сортировки, для которых характерно наличие такого объема данных, который не представляется возможным целиком разместить в оперативной памяти. В третьей главе приводятся различные алгоритмы поиска информации в упорядоченных и неупорядоченных массивах. Далее в пособии вводится понятие хеш-функции и предлагаются ряд алгоритмов для работы с ними. Четвертая глава рассматривает алгоритмы на графах. К ним относятся обход графа, поиск кратчайшего пути и задача о максимальном потоке. В конце пособия по итогам всех приведенных тем предлагается список задач для лабораторных работ по курсу.

Данное пособие представляет собой первую часть лекционного курса составителя по дисциплине “Методы программирования” для специальности 075200 – Компьютерная безопасность. При подготовке данного методического пособия активно использовалась литература, приведенная в библиографическом списке, а также материалы internet-сайтов, таких как http://www.citforum.ru и http://algoritm.manual.ru. Составитель данного пособия никоим образом не собирается посягать ни на авторство алгоритмов, ни на авторство материалов, приводимых в данном пособии. В начале каждой темы дается ссылка на первоисточник с тем, чтобы студент в случае необходимости смог обратиться за дополнительной информацией. Библиографический список данного пособия намеренно не содержит слишком большое количество монографий, чтобы акцентировать внимание студентов на самых главных их них. При желании можно открыть последнюю страницу любой из приведенных монографий с тем, чтобы получить более развернутый список литературы.

Структуры данных

Структуры данных и алгоритмы служат теми материалами, из которых строятся программы [1].

Под структурой данных в общем случае понимают множество элементов данных и множество связей между ними. Такое определение охватывает все возможные подходы к структуризации данных, но в каждой конкретной задаче используются те или иные его аспекты. Поэтому вводится дополнительная классификация структур данных, направления которой соответствуют различным аспектам их рассмотрения. Прежде чем приступать к изучению конкретных структур данных, необходимо привести их общую классификацию по нескольким признакам.

Понятие "физическая структура данных" отражает способ физического представления данных в памяти машины и называется еще структурой хранения, внутренней структурой или структурой памяти. В настоящем пособии физическая структура данных не рассматривается.

Рассмотрение структуры данных без учета ее представления в машинной памяти называется абстрактной или логической структурой. В общем случае между логической и соответствующей ей физической структурами существует различие, степень которого зависит от самой структуры и особенностей той среды, в которой она должна быть отражена.

Различаются простые (базовые, примитивные) структуры (типы) данных и интегрированные (структурированные, композитные, сложные). Простыми называются такие структуры данных, которые не могут быть расчленены на составные части, большие, чем биты. С логической точки зрения простые данные являются неделимыми единицами. Интегрированными называются такие структуры данных, составными частями которых являются другие структуры данных – простые или в свою очередь интегрированные. Интегрированные структуры данных конструируются программистом с использованием средств интеграции данных, предоставляемых языками программирования.

Весьма важный признак структуры данных - ее изменчивость - изменение числа элементов и (или) связей между элементами структуры. В определении изменчивости структуры не отражен факт изменения значений элементов данных, поскольку в этом случае все структуры данных имели бы свойство изменчивости. По признаку изменчивости различают структуры статические, полустатические и динамические. Классификация структур данных по признаку изменчивости приведена ниже на рис. 1. Базовые структуры данных, статические, полустатические и динамические характерны для оперативной памяти и часто называются оперативными структурами. Файловые структуры соответствуют структурам данных для внешней памяти.

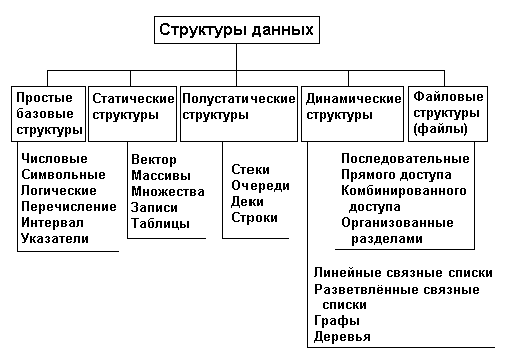
Рис. 1. Классификация структур данных

Важный признак структуры данных - характер упорядоченности ее элементов. По этому признаку структуры можно делить на линейные и нелинейные структуры.

В зависимости от характера взаимного расположения элементов в памяти линейные структуры можно разделить на структуры с последовательным распределением элементов в памяти (векторы, строки, массивы, стеки, очереди) и структуры с произвольным связным распределением элементов в памяти (односвязные, двусвязные списки). Пример нелинейных структур - многосвязные списки, деревья, графы.

В языках программирования понятие "структуры данных" тесно связано с понятием "типы данных". Любые данные, т.е. константы, переменные, значения функций или выражения, характеризуются своими типами.

Информация по каждому типу однозначно определяет :

1) структуру хранения данных указанного типа, т.е. выделение памяти и представление данных в ней, с одной стороны, и интерпретация двоичного представления, с другой;

2) множество допустимых значений, которые может принимать тот или иной объект описываемого типа;

3) множество допустимых операций, которые применимы к объекту описываемого типа.

Далее в текущем разделе приводится описание интегрированных структур данных, которые широко распространены на практике и используются в настоящем пособии.

1.1 Треугольные массивы [2]

Очень часто на практике приходится иметь дело с треугольными массивами. Примером могут служить операции с симметричными матрицами, которые часто появляются в сетевых задачах и задачах упругости. Если хранить соответствующую структуру данных в двумерном массиве, это вызовет излишний расход машинной памяти. Так, при размере матрицы в 1000 строк придется хранить более полумиллиона ненужных элементов.

Массив А:

A[1,0]
A[2,0]	A[2,1]
A[3,0]	A[3,1]	A[3,2]

Массив В:

A[1,0]

A[2,0]

A[2,1]

A[3,0]

A[3,1]

A[3,2]

Рис. 2. Упаковка треугольного массива в одномерный массив

Самым оптимальным выходом в данной ситуации является создание одномерного массива В и упаковка в него значимых элементов массива А (см. рис. 2). Формула для преобразования A[i,j] в B[x] имеет вид: x=[i(i-1)/2+j] для i>j. Выражение в квадратных скобках в данной формуле означает операцию взятия целой части числа.

Если треугольный массив содержит ненулевые диагональные элементы, то для его хранения в одномерном массиве можно также использовать предыдущую формулу, если перед ее применением увеличить значение индекса i на единицу.

При практической реализации данного способа хранения представляется целесообразным в качестве В использовать динамический массив. Безусловно, обращение к его элементам будет происходить медленнее, чем к элементам массива A. Поэтому использование данного алгоритма является оправданным лишь для больших массивов, когда появляются проблемы с хранением информации.

1.2 Списки [3]

В данном разделе описываются методы создания динамических списков. Различные виды списков имеют различные свойства. Некоторые из них достаточно просты и функционально ограничены. Другие же, такие, как циклические, двусвязные списки и списки с указателями, сложнее и поддерживают более развитые средства управления данными.

Простые списки

Если в программе нужен список постоянного размера, проще всего его реализовать при помощи массива. В этом случае можно легко исследовать элементы списка в цикле. Во многих программах приходится иметь дело со списками, размер которых может постоянно изменяться. Можно создать массив, размер которого будет максимально возможным размером списка, но такое решение для большинства случаев не является оптимальным. Ниже представлен фрагмент кода программы, соответствующий данному случаю.

const

MaxArrayIDX=1000;

type

TIntArray=array[1..MaxArrayIDX] of integer;

PIntArray=^TIntArray;

var Items:PIntArray;

procedure CreateAndFillArray(NumItems:integer);

var i:integer;

begin

GetMem(Items,NumItems*SizeOf(Integer));

for i:=1 to NumItems do Items^[i]:=i;

end;

procedure DisposeArray;

begin

FreeMem(Items);

end;

Приведенный выше код является примером того, как не надо писать программы, так как данный код имеет потенциальные возможности для ошибок в программе. Дело в том, что в приведенном фрагменте массив воспринимается как указатель, содержащий MaxArrayIDX ячеек. Если происходит выделение памяти только для десяти элементов, то исполнимая программа не определит попытку доступа к 100-му элементу массива как ошибку. В лучшем случае обращение к данной ячейке аварийно остановит программу. В худшем случае это вызовет неявный сбой, который будет достаточно сложно найти. Подобные же проблемы возникнут при неверном задании нижней границы массива.

Несмотря на подстерегающие опасности изменение размеров массива– очень мощная методика, позволяющая достигать большой производительности. Среда программирования Delphi, начиная с версии 4.0, поддерживает встроенный механизм динамических массивов.

Ниже представлен код программы, реализующий создание и уничтожение массивов данного типа.

var Items:array of integer;

procedure CreateAndFillArray(NumItems:integer);

var i:integer;

begin

SetLength(Items,NumItems);

for i:=Low(Items) to High(Items) do Items[i]:=i;

end;

procedure DisposeArray;

begin

SetLength(Items,0);{или Items:=nil}

end;

Список переменного размера

С помощью динамических массивов легко построить простой список переменного размера. Новый элемент в список добавляется следующим образом. Создается новый массив, который на один элемент больше старого. Далее копируются элементы старого массива в новый и добавляется новый элемент. Затем освобождается старый массив и устанавливается указатель массива на новую страничку памяти. Если использовать динамические массивы, реализованные в Delphi, то алгоритм добавления элемента в конец списка будет еще проще - при изменении размера массива программа автоматически создает новый и копирует в него содержимое старого:

var List:array of integer;

procedure AddItem(new_item:integer)

begin

// Увеличиваем размер массива на 1 элемент.

SetLength(List,Length(List)+l);

// Сохранение нового элемента.

List[High(List)]:=new_item;

end;

Эта простая схема хорошо работает для небольших списков, но у нее есть два существенных недостатка. Во-первых, приходится часто менять размер массива. Чтобы создать список из 1000 элементов, необходимо 1000 раз изменить размеры массива. Ситуация осложняется еще тем, что чем больше становится список, тем больше времени потребуется на изменение его размера, поскольку необходимо каждый раз копировать растущий список в заново выделенную память[4]. Чтобы размер массива изменялся не так часто, при его увеличении можно вставлять дополнительные элементы, например, по 10 элементов вместо 1. Если впоследствии возникает необходимость добавлять новые элементы к списку, то они разместятся в уже существующих в массиве неиспользованных ячейках, не увеличивая размер массива. Точно так же можно избежать изменения размера каждый раз при удалении элемента из списка. Свободные ячейки позволяют избежать изменения размеров массива всякий раз, когда необходимо добавить или удалить элемент из списка.

Неупорядоченные списки

В некоторых приложениях требуется удалять одни элементы из середины списка, добавляя другие в его конец. Это может быть в случае, когда порядок элементов не важен, но необходимо иметь возможность удалять определенные элементы из списка. Списки данного типа называются неупорядоченными списками.

Неупорядоченный список должен поддерживать следующие операции:

· добавление элемента к списку;

· удаление элемента из списка;

· определение наличия элемента в списке;

· выполнение каких-либо операций (например, печати или вывода не дисплей) для всех элементов списка.

Для управления подобным списком можно немного изменить простую схему, представленную в предыдущем разделе. Когда удаляется элемент из середины списка, оставшиеся элементы сдвигаются на одну позицию, заполняя образовавшийся промежуток. Однако удаление элемента массива подобным способом может занимать много времени, особенно если этот элемент находится в начале списка. Чтобы удалить первый элемент массива, содержащего 1000 записей, необходимо сдвинуть 999 элементов на одну позицию влево. Гораздо быстрее удалять элементы при помощи простой схемы “сборки мусора“. Вместо удаления элементов из списка можно их отметить как неиспользуемые. Если элементы списка – данные простых типов, то их можно маркировать с помощью так называемого "мусорного" значения. Если элементы списка - это структуры, определенные оператором tуре, то можно добавить к ним новое логическое поле IsGarbage. При удалении элемента из списка значение поля IsGarbage устанавливается в True.

Через некоторое время список может переполниться "мусором", в результате чего будет тратиться большое количество машинного времени на пропуск ненужных элементов, чем на обработку реальных данных. Во избежание такой ситуации надо периодически выполнять процедуру сборки мусора. Эта процедура перемещает все непомеченные элементы в начало массива. После этого они добавляются к неиспользуемым элементам в конце массива. Когда вам потребуется включить в список дополнительные элементы, можно повторно использовать помеченные ячейки без изменения размера массива. После добавления дополнительных неиспользуемых записей к другим свободным ячейкам полный объем свободного пространства может стать слишком большим. В этом случае следует уменьшить размер массива, чтобы освободить память.

Связанные списки

В отличие от неупорядоченных списков, элементы которых никак не связаны друг с другом [5], отличительной особенностью данного вида списков является именно наличие связей между его элементами. На рис. 3 представлена структура односвязного списка.

Рис. 3. Структура односвязного списка

В нем поле INF – информационное поле, данные, NEXT – указатель на следующий элемент списка. Для последовательного обхода всех элементов списка необходимо иметь указатель на его вершину. Для того чтобы корректно обрабатывать случай конца списка, лучше всего в поле указателя последнего элемента списка записывать значение пустой ссылки.

Данный вид списка обладает некоторыми важными свойствами. Во-первых, в начало данного списка очень просто добавлять новые элементы (рис. 4). Для этого необходимо создать новую ячейку, указывающую на текущую вершину списка, а затем сделать так, чтобы новой вершиной списка стала только что созданная ячейка. Соответствующий код на Pascal для этой операции достаточно прост:

new_cell^.NextCell:=top_cell;

top_sell:=new_cell;

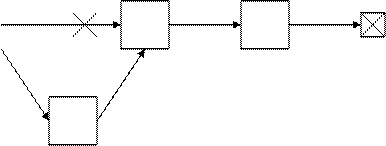
Рис. 4. Добавление элемента в начало связанного списка

Так же легко осуществляется вставка нового элемента и в середину связанного списка. Предположим, необходимо добавить новый элемент после ячейки, на которую указывает переменная after_me. В этом случае соответствующий код на Pascal имеет вид:

new_cell^.NextCell:=after_me^.NextCell;

after_me^.NextCell:=new_cell

Процедура удаления элемента как из начала, так и из середины списка также не вызывает никаких сложностей.

Обычно связанные списки удобнее, но списки на базе массивов имеют одно существенное преимущество – они используют меньше памяти. Каждый из указателей занимает дополнительные четыре байта памяти. Кроме этого, доступ к элементам связанного списка происходит последовательно, что занимает лишнее машинное время.

Если в программе возникает необходимость обхода элементов списка как в прямом, так и обратном порядке, то для этого случая представляется целесообразным использование другой разновидности связанных списков, а именно, двусвязных списков. Каждый элемент списка хранит указатель на следующий элемент и на предыдущий (рис. 5).

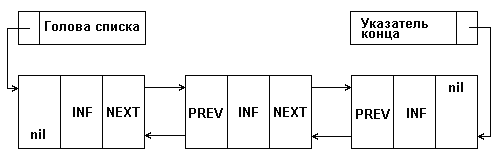
Рис. 5. Представление двусвязного списка

1.3 Стеки [6]

Стек - такой последовательный список с переменной длиной, включение и исключение элементов из которого выполняются только с одной стороны списка, называемого вершиной стека.

Примеры стека: винтовочный патронный магазин, тупиковый железнодорожный разъезд для сортировки вагонов. Традиционно операция помещения значения в стек называется pushing (проталкивание), а извлечение из стека – popping (выталкивание). Для реализации стека можно использовать как динамические массивы, так и односвязный список. Так, реализация с помощью динамических массивов имеет вид:

var Stack:array of integer;

procedure Push(value:integer);

begin

SetLength(Stack, Length(Stack)+1);

Stack[High(Stack)]:=value

end;

function Pop:integer;

begin

Result:=Stack[High(Stack)];

SetLength(Stack, Length(Stack)-1)

end;

Данный способ реализации стека сохраняет все недостатки, которые имели место для неупорядоченных списков, реализованных подобным образом. Однако вместе с тем допускает и те же возможности для его оптимизации, т.е. изменение размеров массива не поэлементно, а сразу для некоторой группы и т.п. Однако все же наиболее приемлемым как с точки зрения затрат памяти, так и с точки зрения скорости работы, способом реализации стека является использование односвязных списков. В этом случае в качестве операции помещения элемента в стек следует использовать процедуру добавления элемента в начало списка, а в качестве операции извлечения элемента из стека следует использовать операцию получения первого его значения с последующим удалением из списка.

1.4 Очереди. Деки. [7]

Очередь или односторонняя очередь - это линейный список, в котором все опе­рации вставки выполняются на одном из концов списка, а все операции удаления (и, как правило, операции доступа к данным) - на другом.

Реализация очередей может быть осуществлена также с помощью динамических массивов или связанных списков. Однако в данном случае использование динамических массивов представляется достаточно затратным с точки зрения расходования вычислительных ресурсов. Ввиду того, что данные должны вводиться с одного конца массива, а удаляться с другого, получается, что необходимо постоянно осуществлять сдвиги элементов массива, даже если после каждой вставки происходит операция удаления из очереди. Поэтому для реализации очередей представляется целесообразным использование именно связанных списков, а из-за того, что должны осуществляться операции на его обоих концах, наиболее подходящими структурами являются двусвязные списки.

Очереди с приоритетом

В данной очереди каждый элемент имеет определенный приоритет. При удалении элементов, в первую очередь удаляются элемент с самым высоким приоритетом. При этом не имеет значения, в каком порядке элементы хранятся в очереди.

Некоторые операционные системы используют очереди с приоритетом для планирования задания. В операционной системе UNIX все процессы имеют разные приоритеты. Когда процессор освобождается, выбирается готовый к исполнению процесс с максимальным приоритетом.

Пожалуй, самый простой способ организации очереди с приоритетами - поместить все элементы в список. Если требуется удалить элемент из очереди, надо найти в списке элемент с наивысшим приоритетом. Чтобы добавить элемент к очереди, необходимо просто разместить новый элемент в начале списка. Если очередь содержит N элементов, требуется O(N) шагов, чтобы определить положение и удалить из очереди элемент с максимальным приоритетом.

В качестве второго способа организации очереди с приоритетом можно также использовать связанный список, однако хранить элементы, располагая их в порядке уменьшения приоритета. Тип данных списка TPriorityCell можно определить следующим образом:

type

PPriorityCell = ^TPriorityCell;

TPriorityCell = record

Value:string; // Данные

Priority:integer; // Приоритет элемента

NextCell:PPriorityCell; // Следующая ячейка

end;

Чтобы добавить элемент в очередь, необходимо найти для него правильную позицию в списке и поместить его туда.

Чтобы удалить из списка элемент с самым высоким приоритетом, достаточно удалить первый элемент в очереди. Поскольку список отсортирован в порядке уменьшения приоритета, первый элемент всегда имеет наивысший приоритет.

1.5 Деревья [8]

Деревья, пожалуй, являются одними из наиболее важных нелинейных структур, которые встречаются при работе с компьютерными алгоритмами.

Формально дерево определяется как конечное множество Т одного или более узлов со следующими свойствами:

a) существует один выделенный узел, а именно- корень данного дерева Т;

b) остальные узлы (за исключением корня) распределены среди m³0 непересекающихся множеств T_1,....T_m, и каждое из этих множеств, в свою очередь, является деревом; деревья Т_1,..., Т_m называются поддеревьями данного корня.

Данное определение является рекурсивным: дерево определено на основе понятия дерева.

На рис. 6 изображено дерево. Корневой узел А соединен с тремя поддеревьями, начинающимися узлами В, С и D. Эти узлы соединены с поддеревьями, имеющими корни в узлах Е, F и G, которые в свою очередь связаны с поддеревьями с корнями Н, I и J.

Данная терминология является смесью терминов, заимствованных из ботаники и генеалогии. Из ботаники взято определение узла, который представляет собой точку, где может возникнуть ветвь. Ветвь описывает связь между двумя узлами, лист - узел, откуда не выходят другие ветви.

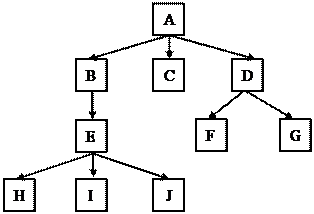
Рис. 6. Дерево

Из генеалогии пришли термины, описывающие отношения. Если узел находится непосредственно над другим, то он называется родительским, а нижний узел называется дочерним. Узлы на пути вверх от узла до корня принято считать предками узла. Например, на рис. 6 предками узла I являются узлы Е, В и А. Все узлы, расположенные ниже какого-либо узла, называются его потомками. На рис. 6 потомками узла В являются узлы Е, Н, I и J. Узлы, имеющие одного и того же родителя, называются сестринскими.

Кроме того, существует несколько понятий, возникших собственно в программистской среде. Внутренний узел - это узел, не являющийся листом. Порядком узла или его степенью называется количество его дочерних узлов. Степень дерева - это максимальный порядок его узлов. Степень дерева, изображенного на рис. 6, равна 3, так как узлы А и Е, имеющие максимальную степень, имеют по три дочерних узла.

Высота узла равна числу его предков плюс 1. На рис. 6 узел Е имеет высоту 3. Высота дерева- это наибольшая высота всех узлов. Высота дерева, изображенного на рис. 6, равна 4.

Дерево степени 2 называется двоичным или бинарным деревом. Деревья степени 3 называются троичными или тернарными. Аналогично дерево степени N называется N-ичным деревом.

Если в расположении узлов дерева имеет значение относительный порядок поддеревьев, то дерево является упорядоченным.

Лес - это множество, не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев.

Между абстрактными понятиями леса и деревьев существует не очень заметная разница. При удалении корня дерева получается лес, и наоборот: при добавлении одного узла в лес, все деревья которого рассматриваются как поддеревья нового узла, получается дерево.

Обход деревьев

Последовательное обращение ко всем узлам дерева называется обходом. Существует несколько последовательностей обхода узлов двоичного дерева. Три самых простых - прямой, симметричный и обратный, которые реализуются с помощью достаточно простых рекурсивных алгоритмов. Для каждого заданного узла алгоритм выполняет следующие действия:

Прямой порядок:

1. Обращение к узлу.

2. Рекурсивный прямой обход левого поддерева.

3. Рекурсивный прямой обход правого поддерева.

Симметричный порядок:

1. Рекурсивный симметричный обход левого поддерева.

2. Обращение к узлу.

3. Рекурсивный симметричный обход правого поддерева.

Обратный порядок:

1. Рекурсивный обратный обход левого поддерева.

2. Рекурсивный обратный обход правого поддерева.

3. Обращение к узлу.

Для дерева, изображенного на рисунке 7, порядок обхода будет следующим:

Рис. 7. Пример дерева для иллюстрации различных методов его обхода

Прямой порядок: A, B, D, С, Е, G, F, H, J

Симметричный порядок: D, B, A, E, G, C, H, F, J

Обратный порядок: D, B, G, E, H, J, F, C, A

Упорядоченные деревья

Двоичные деревья - обычный способ хранения и обработки информации в компьютерных программах. Если использовать внутренние узлы дерева, чтобы обозначить утверждение "левый дочерний узел меньше правого", то с помощью двоичного дерева можно построить сортированный список. На рис. 8 показано двоичное дерево, хранящее сортированный список с числами 1,2,4,6,7,9.

Рис. 8. Упорядоченный список 1, 2, 4, 6, 7, 9

Добавление элементов

Алгоритм добавления нового элемента в такой тип деревьев достаточно прост. С начала берется корневой узел. Далее следует по очереди сравнивать значения всех узлов со значением нового элемента. Если новое значение меньше или равно значению в рассматриваемом узле, то необходимо продолжать движение вниз по левой ветви. Если новое значение больше значения узла, то переходить следует вниз по правой ветви. Если достигнут конец дерева [9], необходимо вставить элемент в эту позицию.

Удаление элементов

Удаление элемента из сортированного дерева немного сложнее, чем добавление. После этой операции программа должна перестроить другие узлы, чтобы сохранить в дереве соотношение "меньше чем". Следует рассмотреть несколько существующих вариантов.

Во-первых, если удаляемый узел не имеет потомков, допустимо просто убрать его из дерева. При этом порядок остальных узлов не изменяется. Во-вторых, если удаляемый узел имеет один дочерний узел, можно заменять его дочерним узлом. При этом порядок потомков данного узла остается так как эти узлы также являются и потомками дочернего узла. На рис. 9 показано дерево, где удаляется узел 4, имеющий только один дочерний узел.

Рис. 9. Удаление узла с единственным потомком

Если удаляемый узел имеет два дочерних, вовсе не обязательно, что один из них займет его место. Если потомки узла также имеют по два дочерних, то для размещения всех дочерних узлов в позиции удаленного узла просто нет места. Чтобы решить эту проблему, необходимо заменить удаленный узел крайним правым узлом дерева из левой ветви. Другими словами, необходимо двигаться вниз от уда­ленного узла по левой ветви. Затем необходимо двигаться вниз по правым ветвям до тех пор, пока не найдется узел без правой ветви. Если найденный узел является листом (на рис. 10 это узел 3), то им следует заменить удаляемый узел.

Рис. 10. Удаление узла с двумя потомком

В случае же когда найденный узел имеет левого потомка тот встает на место заменяемого узла.

Сбалансированные деревья

После выполнения ряда операций c упорядоченное дерево, таких как вставка и удаление узлов, оно может стать несбалансированным. Если подобное происходит, алгоритмы обработки дерева становятся менее эффективными. При сильной степени разбалансировки дерево фактически вытягивается в линейный список [10] , а у программы, использующей дерево, может резко снизиться производительность. В данном разделе рассматриваются методы сохранения баланса дерева даже при постоянной вставке и удалении элементов.

Балансировка

Форма упорядоченного дерева зависит от порядка добавления элементов. Высокие, тонкие деревья могут иметь глубину до O(N), где N- число узлов дерева. Добавление или размещение элемента в таком разбалансированном дереве может занимать О(N) шагов. Даже если новые элементы размещаются беспорядочно, в среднем они дадут дерево с глубиной N/2, обработка которого потребует так же порядка О(N) операций.

Ниже рассматриваются методы, которые позволяют поддерживать деревья в сбалансированном состоянии при вставке и удалении узлов.

AVL-деревья

AVL-деревья были названы по имени российских математиков Адельсона-Вельского и Ландау, которые их изобрели. В каждом узле AVL-дерева глубина левого и правого поддеревьев отличаются не более чем на единицу. На рис. 11 изображено несколько AVL-деревьев.

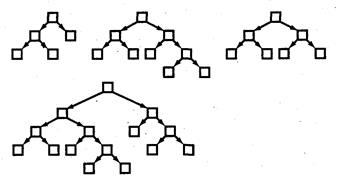
Рис. 11. AVL – деревья

AVL-дерево имеет глубину O(log₂N). Следовательно, и поиск узла в AVL-дереве занимает время порядка O(log₂N), что при больших N существенно меньше, чем O(n).