Этапы выполнения лабораторной работы

ТАБЛИЧНЫЙ ПРОЦЕССОР ЕХСEL

Вариант №1

Выполнил: студент группы 4109 Петров И.А.

Проверил: Суздальцев В.А.

Казань. 2013

ЦЕЛЬ ЛАБОРАТОРНОЙ РАБОТЫ:

Научиться выполнить вычисления значений функции на заданном сегменте. Найти точки экстремума функции. Вычислять значение производной функции и определять значение интеграла используя программу Microsoft Excel.

Краткое теоритическое обоснование.

EXCEL – программное приложение, предназначенное для автоматизированной обработки табличных документов требующих многократных расчетов с большими объемами данных. Такие программы называют табличными процессорами или электронными таблицами.

Создание таблицы начинается с ввода заголовка. Затем вводятся названия для каждой графы таблицы. Заголовок графы может занимать несколько ячеек таблицы, если для него недостаточно одной строчки.

Ввод исходных данных. В каждой ячейке размещается одна величина, при этом с помощью команды Форматможноизменить формат представления данных ячейки или блока ячеек, а также обеспечить выравнивание данных.

Вводимая или введенная в текущую ячейку величина отражается в строке ввода, расположенной под строкой инструментов над рабочим листом книги. В этой строке может быть выполнено редактирование содержимого текущей ячейки по обычным правилам. Для редактирования необходимо предварительно зафиксировать курсор с помощью указателя мыши в строке ввода.

Для вставки/удаления строки или столбца можно воспользоваться командой Вставка.При этом вставляется строка или столбец перед текущей строкой (столбцом), удаляется выделенная строка (столбец) или выделенный диапазон строк (столбцов).

Для удаления содержимого ячейки или блока ячеек необходимо выделить нужный фрагмент и нажать клавишу Delete или выполнить вырезку.

Ввод формулы. Формула составляется из констант и имен ячеек с использованием знаков операций. Для указания порядка действий используются скобки по обычным правилам. Самым первым символом в формуле должен быть знак равенства, пример: =(А4+В4)/2.

При вводе формулы после нажатия клавиши ввода происходит вычисление значения ячейки, которое повторяется каждый раз при изменении величин, входящих в формулу. Например, если в ячейке С4 набирается строка =С2+С3, то после нажатия клавиши ввода в ячейке С4 появится сумма значений ячеек С2 и С3.

При наборе сложных формул можно воспользоваться функциями, которые выбираются из списка с помощью команд Вставка/Функция. В качестве аргументов функций могут быть указаны ячейки или блоки. Например, функция СУММА(В4:В10) обеспечивает вычисление суммы содержимого ячеек блока В4:В10, т.е. суммы В4+В5+В6+В7+В8+В9+В10.

Автосуммирование. Автосуммирование удобно применять при вы­числении итоговых сумм по столбцам или строкам. Самый простой способ – выделить ячейку для результата, после чего дважды щелкнуть кнопку автосуммирование (кнопка с изображением математического знака суммы). В ячейке появится формула с функцией СУММА. Другим способом является выбор функции через команды Вставка, Функция.

Для неоднозначных вычислений с использованием ветвления формула представляет структуру выбора, начинается со слова ЕСЛИ и включает условие, например:

=ЕСЛИ(В7>100 ; А7+В7 ; А7+В7+С7).

В этом случае перед вычислением происходит проверка условия В7>100. При истинном значении обеспечивается вычисление по первой из указанных формул (А7+В7), при ложном – по второй.

Копирование формулы. Копирование формул применяется, если для вычисления значений множества ячеек должна быть применена аналогичная формула. Один из способов копирования формулы заключается в следующем. Сначала следует выделить копируемую формулу, выбрать команду Копировать в менюПравка. После этого выделить блок ячеек, куда нужно скопировать формулу и воспользоваться командой Вставить из меню Правка. После копирования нужно отменить выделение блока. При копировании автоматически корректируются номера ячеек в формулах и происходит автоматическое вычисление.

Обрамление таблицы При обрамлении таблица оформляется с помощью линий, образующих рамки. Предварительно следует выделить обрамляемый блок, затем последовательно выполнить команды Формат/ Ячейки/ Граница. После этого с помощью диалогового окна выбирается расположение обрамления, цвет, толщина линий. Для удаления рамок повторяются точно те же действия, но выбирается первое окно при указании толщины линии ( вариант «нет»).

Формирование диаграммы. Многие табличные данные удобно иллюстрировать с помощью графического материала. Для этого предварительно в таблице выделяется множество значений которые будут представлены в виде диаграммы, поле чего нажимается кнопка Диаграмма.

Задания.

Выполнить работу на ЭВМ, используя программу Microsoft Excel.

1. Вычислить значение функции на сегменте [a, b] c шагом 0.1.

2. Найти точки экстремума функции на сегменте [a, b].

3. Вычислить значение производной функции на сегменте [a, b] c шагом 0.1

4. Определить значение интеграла на сегменте [a, b] c шагом 0.1:

.

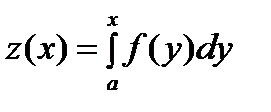Вариант 1.

Функция f(x)= ax+ b´sin(x) +exp(a/(x+b(lgx))). (1)

Заданный сегмент [6;8].

ЭТАПЫ ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ.

1) Для того то, что бы вычислить значение функции на сегменте [6, 8] c шагом 0.1, заполняем в таблице столбец x соответствующими значениями от 6 до 8 (см. рис.1).

Рис.1.

Функцию (1) записываем в столбец y(x) в виде «=(6*A2+8*SIN(A2)+EXP(6/(A2+8*LN(A2))))» и выполняем вычисления подставляя вместо A2 значения стоящие в столбце x, а вместо a и b значения равные 6 и 8 (см. рис. 2).

Рис.2.

Таким образом, вычисляем значение функции на сегменте [6, 8] c шагом 0.1.

График функции показан на рисунке 3.

Рис.3.

2) Нахождение экстремумов функции.

Для того, чтобы найти максимум функции необходимо в столбце МАХ написать в следующую ячейку выражение «=МАКС (С2:С22)» и нажав Enter получается максимальное значение (см. рис. 4).

Для того, чтобы найти минимум функции необходимо в столбце МIN написать в следующую ячейку выражение «=МИН (С2:С22)» и нажав Enter получается минимальное значение (см. рис. 4).

Рис.4.

Для того, чтобы вычислить значение производной функции на сегменте [6.1, 8.1] c шагом 0.1, заполняем в таблице столбец х+dx соответствующими значениями от 6.1 до 8.1 (см. рис.5).

Рис.5.

Функцию (1) записываем в столбец у (х+dx) в виде «=(6*B2+8*SIN(B2)+EXP(6/(B2+8*LN(B2))))» и выполняем вычисления подставляя вместо х значения стоящие в столбце х+dx, а вместо a и b значения равные 6 и 8 (см. рис. 6).

Рис.6.

Таким образом, вычисляем значение функции на сегменте [6.1, 8.1] c шагом 0.1.

Для того что вычислить производную этой функции не обходимо из у (x+dx) вычесть y (x) и полученную разность разделить на 0,1. В таблице это будет выглядеть следующим образом: «=(D2-C2)/0,1». После этого выполняется вычисления (см. рис. 7).

Рис.7.

График зависимости области определения функции от области значения показан на рисунке 8.

Рис.8.

График зависимости интеграла показан на рис.10.

Рис.10.

3) Определение значения интеграла на сегменте [6, 8] c шагом 0.1:

.

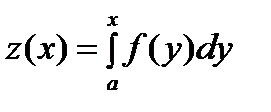Для определения значения интеграла на сегменте [6, 8] c шагом 0.1 применим правило вычисления с помощью прямоугольников. Для этого необходимо значение y (x) умножить на 0,1. Полученное значение будет значением интеграла на интервалах dx. Далее суммируем значения полученных площадей.

(см. рис. 9).

Рис.9.

Вывод: в этой лабораторной работе мы научились выполнить вычисления значений функции на заданном сегменте, находить точки экстремума функции. Вычислять значение производной функции и определять значение интеграла используя программу Microsoft Excel.