Естирование многослойного персептрона

ель работы

Изучение режима функционирования нейронной сети (НС), определение качества обобщения сети по тестовой выборке. Изучение принципов построения оптимальной структуры многослойного персептрона (МСП) для заданного класса задач. Изучение влияния модели нейрона на качество обучения нейронной сети. В результате выполнения работы студент знакомится с режимом функционирования НС, на основе полученных экспериментальных данных обучается определять оптимальную по нескольким параметрам структуру МСП, оценивать экспериментальные зависимости.

адание

2.1. Сформировать множество входных данных для определения качества обобщения НС – тестовое множество (ТМ).

2.2. Протестировать нейронную сеть в режиме функционирования на тестовом множестве. Оценить качество обобщения НС.

2.3. Исследовать зависимость времени и качества обучения МСП от параметров структуры нейронной сети.

2.4. На основе полученных экспериментальных зависимостей определить оптимальную конфигурацию МСП.

2.5. Построить оптимальную структуру МСП и обучить ее. Оценить качество обучения НС.

2.6. Сравнить полученные результаты с результатами обучения исходной нейронной сети (построенной в лабораторной работе 2.2).

2.7. Протестировать оптимальную нейронную сеть в режиме функционирования на тестовом множестве. Оценить качество обобщения оптимальной НС.

2.8. Сравнить полученные результаты с результатами тестирования исходной нейронной сети (построенной в лабораторной работе 2.2).

абочее место

Работы выполняются на ПЭВМ. При выполнении работы используется программа NeuroPro 0.25.

еоретическая часть

естирование многослойного персептрона

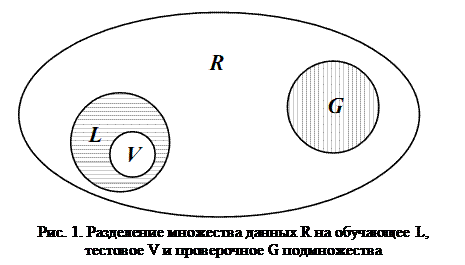
Качество обобщения данных нейронной сетью можно определить, наблюдая за величиной ошибки, вычисленной на тестовом множестве. Пусть существует множество данных, подчиняющихся правилу R. Тогда при обучении НС на данных из этого множества возникает задача разделения данного множества на обучающее L, тестовое V и проверочное G подмножества. Пример разделения приведен на рис. 1.

Элементы L и G должны быть типичными элементами множества R. Способность отображения сетью элементов L является показателем ее обученности и характеризуется ошибкой (погрешностью) обучения. Способность распознавания данных подмножества G показывает ее возможности обобщения знаний и описывается ошибкой (погрешностью) обобщения. Для верификации качества обучения НС в составе L выделяется определенное подмножество контрольных (тестовых) данных V.

Тестовое множество составляется чаще всего на основе обучающего множества. Его мощность составляет от 20% до 50% от обучающего множества.

Тестирование НС выполняется в нейроэмитаторе на тестовом множестве в режиме тестирования (без обучения). По результатам тестирования вычисляется ошибка обобщения для проведения сравнения с результатами обучения сети.

4.2. Оптимизации МСП

Результаты тестирования исходной сети, как правило, оказываются не удовлетворительными. Необходимо наилучшим образом подобрать параметры сети. Это достигается в процессе ее оптимизации.

Для решения какой-либо задачи с применением НС нужно, прежде всего, создать структуру сети, адекватную поставленной задаче (аналогично составлению соответствующей программы для универсальной ЭВМ). Это предполагает выбор количества слоев НС и числа нейронов в каждом слое, а также задание параметров модели нейрона и алгорима обучения сети.

Количество точек ветвления на входе сети определяется размерностью N входного вектора А_i , количество нейронов выходного слоя – размерностью M ожидаемого (целевого) вектора D_i. Определение минимального числа скрытых слоев основано на использовании свойств аппроксимирующих функций.

Для непрерывного преобразования X®Y достаточно иметь один скрытый слой с K=(2N + 1) нейронами, в случае дискретного преобразования необходимое число скрытых слоев возрастает до двух. В практических реализациях ИНС как количество скрытых слоев, так и число нейронов в них могут отличаться от теоретически предлагаемых. За немногими исключениями, чаще всего используются НС, имеющие один (максимум – 2) скрытый слой, в котором от N до 3N нейронов.

Определение оптимального числа нейронов основано на способности НС обобщению полученных знаний, то есть выдаче правильных результатов при подаче на ее вход данных, не входящих непосредственно в обучающую выборку.

При обучении НС оказывается, что количество весов T_w сети (число степеней свободы) и число примеров из обучающей выборки р тесно связаны. Например, если бы целью обучения НС было только запоминание входных векторов А_i, тогда достаточно было бы p=T_w. Однако такая сеть не будет обладать свойством обобщения и сможет только восстанавливать данные. Для обретения обобщающих свойств НС необходимо выполнение p > Tw, чтобы веса сети адаптировались не к уникальным выборкам, а к их статистически усредненным совокупностям.

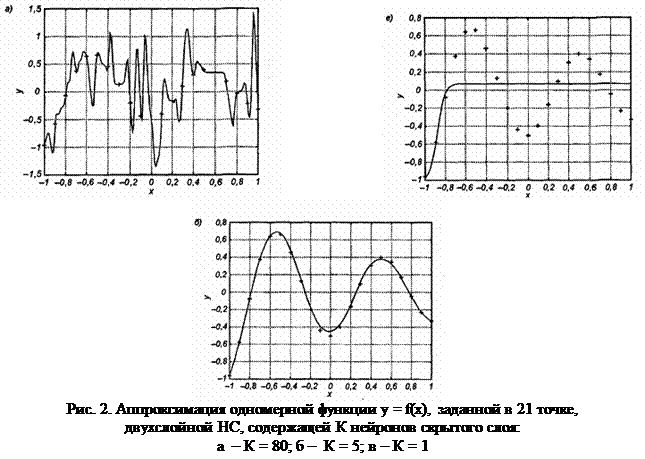
Наглядная графическая иллюстрация способности НС к обобщению показана на рисунке 2 на примере аппроксимации одномерной функции двухслойной НС. При избыточном числе нейронов и весов проявляется эффект гиперразмерности НС (или переобучения), когда минимизация ошибки обучения на относительно малом числе обучающих примеров провоцирует случайный характер значений многих весов, что при переходе к тестовым векторам обусловило значительное отклонение фактических значений Y_i от ожидаемых D_i (рис. 2, а). Уменьшение количества скрытых нейронов до оптимального значения (рис. 2, б) обеспечивает и малую погрешность обучения, и высокую степень обобщения. Дальнейшее уменьшение К привело к потере НС способности восстанавливать обучающие данные (рис. 2, в).

Методика оптимизации МСП

Параметров, по которым можно проводить оптимизацию МСП очень много. Сюда относятся не только параметры структуры сети, но также параметры формального нейрона, алгоритма обучения, алгоритмов пред и пост обработки обучающей выборки. В данной работе предлагается учитывать при оптимизации следующие параметры структуры МСП и формального нейрона:

· количество слоев нейронной сети;

· число нейронов в скрытых слоях (для каждого слоя);

· характеристику активационной функции с для каждого слоя (диапазон изменения параметра с – от 0,01 до 1.).

Оптимизацию следует проводить комплексно. При этом необходимо последовательно фиксировать параметры оптимизации, исследуя все возможные их комбинации. Результаты экспериментов удобнее сводить в единую таблицу (см. табл. 1).

Порядок фиксирования параметров следующий: 1) количество слоев сети, 2) количество нейронов в каждом слое, 3) характеристика активационной функции с. Текущие значения параметров оптимизации образуют комплексный показатель (х_i). Исследование начинают с однослойной сети, где число нейронов определяется длиной целевого вектора (n)

В результате необходимо построить три графика:

- первый – зависимость количества правильно решенных примеров от комплексного показателя;

- второй – зависимость времени обучения от комплексного показателя;

- третий – зависимость количества циклов обучения от комплексного показателя.

Значение количества циклов обучения используют для обоснования выбора равнозначных экстремумов. Если обучение сети происходит меньше, чем за 1 минуту, то зависимость времени обучения от комплексного показателя исследовать нет необходимости.

После проведения экспериментов с однослойной сетью по графикам определяется оптимальное значение характеристики активационной функции с для данного слоя. При исследовании 2-х слойной сети этот показатель фиксируется (для последнего слоя) и т.д. Если наблюдается тенденция нахождения экстремума характеристики с в более узком, чем предлагаемый диапазон значений (0,01-1), то можно существенно сократить количество опытов.

Таблица 1

количество слоев	число нейронов	хар-ка активационной функции с (для нейронов первого слоя)	комплексный показатель
	n	0,01	х1
0,05	х2
0,2	х3
0,3	х4
0,4	х5
0,5	х6
0,6	х7
0,7	х8
0,8	х9
0,9	х10
	х11
	1/n	0,01	х12
0,05	х13
0,2	х14
0,3	х15
0,4	х16
0,5	х17
0,6	х18
0,7	х19
0,8	х20
0,9	х21
	х22
2/n	0,01	х23
0,05	х24
0,2	х25
0,3	х26
0,4	х27
0,5	х28
0,6	х29
0,7	х30
0,8	х31
0,9	х32
	х33
…	…	…	…	…

После определения оптимальной конфигурации НС на каждом шаге выполняется тестирование НС для вычисления ошибки обобщения и определения направления оптимизации.

орядок выполнения работы

5.1. На отдельном листе исходного xls-файла сформировать множество входных данных для определения качества функционирования оптимальной НС – тестовое множество. В отчете описать параметры ТМ и логику его составления.

5.2. Подать на вход МСП тестовое множество. Сохранить результаты работы НС на отдельном листе исходного xls-файла.

5.3. По полученным результатам функционирования в табличном редакторе Excel рассчитать относительную ошибку обобщения (в процентах).

5.4. Построить гистограмму распределения средней относительной ошибки предсказания сети на этапе тестирования (средняя ошибка для каждого класса (образа). По гистограмме сделать вывод о качестве обобщения НС. Сравнить с результатами обучения.

5.5. С помощью программы-эмулятора НС NeuroPro 0.25 провести эксперименты по определению зависимостей времени обучения, количества циклов обучения, количества правильно решенных примеров от параметров структуры нейронной сети.

Рекомендуемые границы изменяемых параметров сети: диапазон изменения параметра с – от 0,01 до 1; количество слоев сети – от 1 до 5. Результаты исследований представить в виде таблиц и графиков.

После каждого этапа оптимизации подать на вход сети тестовое множество для определения направления оптимизации.

5.6. Сделать выводы по полученным зависимостям, на основании которых определить параметры оптимальной структуры МСП.

5.7. Построить оптимальную структуру многослойного персептрона.

5.8. Обучить нейронную сеть, используя полученные оптимальные значения.

5.9. Полученную нейронную сеть сохранить в нейропроекте под другим именем.

5.10. Сохранить все результаты обучения нейронной сети на отдельном листе xls-файла, где находится Ваша обучающая выборка, результаты обучения и тестирования исходной НС.

5.11. По полученным результатам обучения в табличном редакторе Excel рассчитать относительную ошибку предсказания на этапе обучения (в процентах).

5.12. Построить гистограммы распределения вероятностей относительной ошибки предсказания оптимальной сети на этапе обучения по каждому классу (образу). По гистограммам сделать вывод о качестве обучения НС и сравнить с результатами обучения исходной НС, полученной в предыдущей лабораторной работе.

5.13. Построить гистограмму распределения средней относительной ошибки предсказания сети на этапе обучения. По гистограмме сделать вывод о качестве обучения НС и сравнить с результатами обучения исходной НС, полученной в предыдущей лабораторной работе.

5.2. Подать на вход оптимизированной НС тестовое множество. Сохранить результаты работы НС на отдельном листе исходного xls-файла.

5.7. Построить гистограмму распределения средней относительной ошибки предсказания оптимизированной сети на этапе тестирования. По гистограмме сделать вывод о качестве обобщения НС. Сравнить с результатами обобщения исходной НС.

одержание отчета

Отчет по третьему занятию лабораторной работы №2 включает рукописный отчет, содержание которого приведено ниже, файл с построенной оптимальной нейронной сетью (формат npp) и файл с обучающей выборкой и результатами обучения и тестирования исходной и оптимальной НС, включая гистограммы (формат xls).

6.1. Исходные данные на лабораторную работу.

6.2. Описание тестовой выборки.

6.3. Гистограмма распределения средней относительной ошибки предсказания сети на этапе тестирования и таблица исходных данных к ней.

6.4.Вывод о качестве обобщения НС в сравнении с результатами обучения НС.

6.5. Параметры обучения, которые не будут изменяться при проведении оптимизации.

6.6. Таблицы с результатами исследований.

6.7. Графики зависимостей времени обучения, количества циклов обучения, количества правильно решенных примеров от комплексного показателя. Рекомендуемые границы изменяемых параметров сети: диапазон изменения параметра с – от 0,01 до 1; количество слоев сети – от 1 до 5.

6.8. Выводы по полученным зависимостям. Параметры оптимальной структуры МСП: число входов и выходов НС, количество слоев, количество нейронов каждого слоя, используемые значения характеристики функции активации на каждом слое.

6.9. Обоснование выбора оптимальной структуры МСП.

6.10. Оптимальная структура многослойного персептрона (при этом использовать элементы современной схемотехники НС).

6.11. Гистограммы распределения вероятностей относительной ошибки предсказания сети на этапе обучения и таблицы исходных данных к ним.

6.12. Гистограмма распределения средней относительной ошибки предсказания сети на этапе обучения и таблица исходных данных к ней.

6.13. Вывод о качестве обучения оптимальной НС. Сравнение с результатами обучения исходной НС.

6.14. Гистограмма распределения средней относительной ошибки предсказания сети на этапе тестирования оптимизированной НС и таблица исходных данных к ней.

6.15.Вывод о качестве обобщения оптимизированной НС в сравнении с результатами обучения НС.