Трехмерные матричные преобразования
Подобно тому, как двумерные преобразования описываются матрицами размером 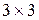 , трехмерные преобразования могут быть представлены матрицами размером
, трехмерные преобразования могут быть представлены матрицами размером 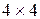 . Тогда трехмерная точка
. Тогда трехмерная точка 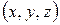 записывается в однородных координатах как
записывается в однородных координатах как 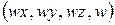 , где
, где 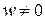 . Для получения декартовых координат надо первые три однородные координаты разделить на
. Для получения декартовых координат надо первые три однородные координаты разделить на 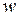 . Два однородных вектора описывают одну декартову точку в трехмерном пространстве, если
. Два однородных вектора описывают одну декартову точку в трехмерном пространстве, если 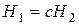 , где
, где 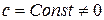 и
и 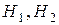 - векторы, записанные в однородных координатах.
- векторы, записанные в однородных координатах.
Матрицы преобразований будем записывать в правосторонней системе координат. При этом положительный поворот определяется следующим образом. Если смотреть из положительной части оси вращения (например, оси 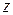 ) в направлении начала координат, то поворот на
) в направлении начала координат, то поворот на 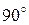 против часовой стрелки будет переводить одну положительную полуось в другую (ось
против часовой стрелки будет переводить одну положительную полуось в другую (ось 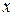 в
в 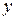 , в соответствии с правилом циклической перестановки).
, в соответствии с правилом циклической перестановки).
Заметим, что на практике удобнее применять левостороннюю систему координат, так как в этом случае удобнее интерпретировать тот факт, что точки с большими значениями 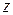 находятся дальше от наблюдателя.
находятся дальше от наблюдателя.
Запишем теперь матрицу трехмерного переноса. Аналогично двумерному случаю:
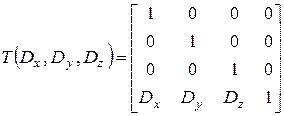 , при этом
, при этом
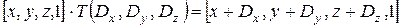 .
.
Операция масштабирования:
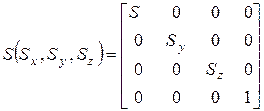
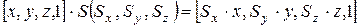
Перейдем к операции поворота; c ней, в трехмерном случае, придется разбираться чуть побольше чем в двумерном. Так как при двумерном повороте в плоскости 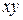 координаты
координаты 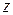 остаются неизменными, то поворот вокруг оси
остаются неизменными, то поворот вокруг оси 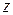 записывается так:
записывается так:
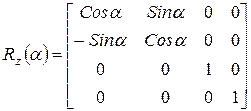 .
.
Матрица поворота вокруг оси 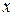 имеет вид:
имеет вид:
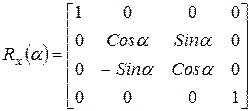 ,
,
и вокруг оси 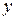 :
:
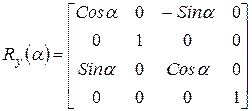
Обратите внимание на смену положения синуса угла с отрицательным знаком в матрице поворота вокруг оси 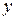 . Правильность этих матриц легко проверить поворотом одного из ортов на
. Правильность этих матриц легко проверить поворотом одного из ортов на 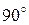 , при этом он должен перейти в следующий по порядку орт на соответствующей координатной оси.
, при этом он должен перейти в следующий по порядку орт на соответствующей координатной оси.
Обратные преобразования будут выражаться обратными матрицами. Для операции переноса надо лишь заменить знаки компонент вектора переноса на противоположные:
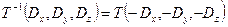 ;
;
для операции масштабирования – на обратные значения:
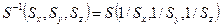 ;
;
для поворота – выбором отрицательного угла поворота:
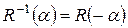 .
.
Результатом нескольких последовательных поворотов будет матрица
 .
.
Здесь верхняя матрица размером 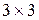 называется ортогональной. Важным ее свойством является то, что обратная к ней матрица является транспонированной:
называется ортогональной. Важным ее свойством является то, что обратная к ней матрица является транспонированной: 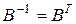 . Это полезно тем, что при вычислениях достаточно поменять индексы местами и обратное преобразование получается автоматически.
. Это полезно тем, что при вычислениях достаточно поменять индексы местами и обратное преобразование получается автоматически.
После перемножения любого числа матриц вида 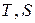 и
и 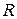 результирующая матрица всегда будет иметь вид:
результирующая матрица всегда будет иметь вид:
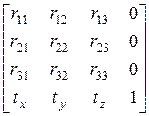 .
.
Здесь верхняя часть размером 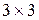 определяет суммарный поворот и масштабирование, а три коэффициента последней строки – суммарный перенос.
определяет суммарный поворот и масштабирование, а три коэффициента последней строки – суммарный перенос.
Вопросы эффективности вычислений
Рассмотрим проблему ускорения вычислений в одной из самых трудоемких операций компьютерной графики – операции поворота точки относительно начала координат. Как было показано ранее, для ее выполнения необходимо произвести 4 операции умножения, 2 операции сложения, а также вычислить значения синуса и косинуса угла поворота. Напомним вид формул поворота:
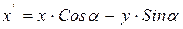
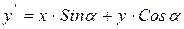
 |
Одним из наиболее часто встречающихся способов ускорения операции поворота является отказ от вычисления синуса и косинуса угла во время выполнения программы, и использование их заранее подсчитанных значений, которые занесены в специальную таблицу. Например, в этой таблице могут храниться значения синусов и косинусов углов поворота с шагом в 1 градус. Тогда целое количество градусов угла поворота может служить в качестве индекса при извлечении соответствующих значений синусов и косинусов из таблицы. Такой прием называется табличным поворотом.
Дополнительным способом ускорения операции поворота является уменьшение количества операций умножения. Рассмотрим вывод формулы О. Бьюнемана с использованием тангенса половинного угла, в которой поворот точки вокруг начала координат производится за 3 операции умножения и 3 операции сложения. Так как на многих микропроцессорах операции умножения выполняются дольше чем операции сложения, то экономия времени достигается за счет уменьшения операций умножения.
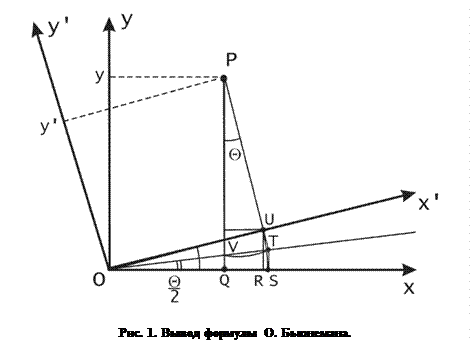
Вывод формулы будем получать из геометрических построений, как показано на рис.28.
Будем искать выражение координат 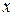 и
и 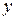 через
через 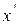 и
и 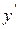 . На оси
. На оси 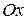 отложим отрезок
отложим отрезок 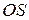 , такой что
, такой что 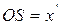 . Тогда
. Тогда 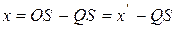 . Здесь отрезок
. Здесь отрезок 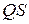 является горизонтальной проекцией отрезка
является горизонтальной проекцией отрезка 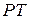 , где
, где 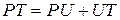 ,
, 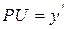 ,
, 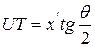
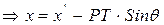 , где
, где 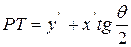 . Теперь, зная
. Теперь, зная 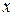 , можно выразить
, можно выразить 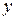 в виде суммы длин отрезков
в виде суммы длин отрезков 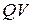 и
и 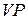 . Так как длины отрезков
. Так как длины отрезков 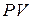 и
и 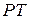 равны как радиусы окружности с центром в точке
равны как радиусы окружности с центром в точке 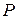 , то
, то 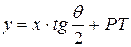 . Обозначим
. Обозначим 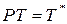 , отсюда следует, что
, отсюда следует, что
 |
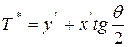 ,
,
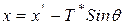 ,
,
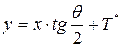
Последние три равенства будем называть формулой О. Бьюнемана.
